1. 引言
随着分子生物学技术的发展,DNA序列等生物数据已经被信息化和网络化,为相关的研究提供了大量的实验数据。事实上,为了从生物数据中挖掘出相关知识,信息生物学研究已经和数据挖掘等信息处理技术有机结合,并且形成了一个新的交叉研究领域。DNA序列是最重要的生物数据之一,通过挖掘DNA序列,研究者可以发现序列数据背后隐藏的有价值的规律,解读相应生物体中的生物特征[1] 。
一般地说,一个DNA序列可以抽象成由固定大小的项目集(字母集)生成的字符串。这样的字符串有2个主要特点:(1)被观察的事务集只有四个字母,即腺嘌呤(A)、胸腺嘧啶(T)、鸟嘌呤(G)和胞嘧啶(C)。这与广泛研究的其它商务数据有很大的差别。例如,在一个购物篮的数据库中,一般涉及成千上万的商品编号,因此被观察的项目全集很大。(2)DNA序列通常都是很长的序列。例如,人类的基因组有大约300万核糖核酸组成。与之相比,通常的购物篮的数据库一般只有10到20的长度。这些特点使得DNA序列的挖掘与普通的事务数据库挖掘有很大的差别。现有的典型的序列挖掘算法,如ApriorAll、GSP等,很难适应DNA序列挖掘的要求。不论是从精度还是效率上都存在问题,因此DNA序列的挖掘需要在相应的挖掘理论及其有效算法方面进一步开展工作。
本文针对DNA序列的特点,设计了一种称为关联矩阵(Association Matrix)的数据结构。由于这种结构能够将超长的DNA序列压缩成空间可控的内存中,因此可以利用它形成新的高效的DNA序列挖掘算法。
2. 相关工作
在生物信息学领域,从DNA序列中寻找相似性片段(子序列)已经被广泛研究。1995年,Hirosawa给出了这一研究领域的基本问题和解决策略[2] 。之后许多学者对DNA序列的相似性进行了相关的研究[3] [4] 。例如,2012年,Papapetrou等认为有三种有效方法可以解决DNA序列的相似性问题:(1) 基于熵的递归分割技术;(2) 基于重要的统计参数指标来归纳;(3) 基于多数投票的策略[4] 。这些方法有一定的使用价值,但是随着研究的深入它们的局限性也逐步暴露出来。由于相似性往往建立在两个序列的长期观察基础上,所以当确认两个生物体的DNA序列是否存在关系时,这些方法的有效性已经得到验证[3] [4] 。事实上,在一个超长的DNA序列中,总是存在特殊的片段(如编码区、poly-区),它们对于了解和解释DNA序列对应的生物学特征是关键的。因此,在一个或者多个超长的DNA序列中发现关键的子序列是一个重要的研究问题。
从数据挖掘的观点来看,从一个DNA序列中寻找关键子序列的问题可以依靠一些序列挖掘技术进行,其中最重要的技术就是频繁(子)序列挖掘。1995年,Agrawal第一次提出并讨论了频繁序列模式挖掘的概念,并且提出的频繁序列模式挖掘算法AprioriAll和AprioriSome,成为这类算法研究的基础[5] 。1996年,Srikant提出了序列模式挖掘的GSP算法,这是一种广度优先的自下而上的算法,而且是目前引用率较高的算法之一[6] 。2000年,Han等提出了另外一种高效的序列模式挖掘算法Free-Span [7] 。之后Han及其相关学者在候选序列集选择等方面进一步改进,形成PrefixSpan等方法[8] [9] 。目前为止,已经出现了很多序列模式挖掘算法[10] -[12] 。Mao等对序列挖掘的基本思想和典型算法给出了比较详尽的介绍[13] 。然而,这些研究都是以商业应用的事务数据库为背景的,不是专门针对DNA序列的。
和本文在方法上高度相关的另一个领域是长序列中挖掘关键子序列的方法研究。Mannila和他的同事已经在这一领域做出了突出贡献。他们的研究是以因特网上的点击事件序列为背景进行的,包括利用贝叶斯挖掘方法实现事件序列分析[14] ;长序列中频繁场景片段(episode)发现[15] ;长序列中强事件序列的发现[16] 。他们的研究为本文DNA序列挖掘提供了可以借鉴的思想。
对本文方法给予启示作用的其它方法还有:长时间序列在线分割方法[17] ;使用路径树查找数据规模较大的序列模式算法[18] ;发现周期性通配符差距的频繁序列发现算法[19] ;Wang等专门为生物信息数据设计的序列挖掘算法[20] 。
3. 关联矩阵设计和DNA序列中的关键序列挖掘算法
众所周知,细胞是用DNA来存储遗传信息的,而DNA则是由两条盘绕在双螺旋结构上的线性链组成。每条链可以看作是由腺嘌呤(A),胸腺嘧啶(T),胞嘧啶(C)和鸟嘌呤(G)形成的线性序列。两条线性链严格遵守碱基配对规则,即A与T、C与G配对出现。例如,一条DNA序列
,与之配对的序列一定是
。对于现代生物计算而言,被符号化的DNA序列一旦被存储在数据库中,特别是成为网络上的公共数据集,那么它们就可以供科研人员研究和使用。
3.1. 关联矩阵
定义1 (DNA序列):给定字符集合E = {A,G,C,T},一个DNA序列被表示为S =
1,e
2,…,e
L>。即对任意的i Î {1,2,…,L},e
iÎE。
定义2 (关联矩阵):给定一个DNA序列s =
1,e
2,…,e
L>,它的关联矩阵定义为(P
ij)
M×4,它列总是大小为4,对应{A,G,C,T}的4个字符;它的行的大小是动态变化的,每行都与s的一个固定长度的子串对应;它的矩阵元素P
ij是行对应的s的子串在列对应的字符前出现的次数。特别地,当行对应的固定子串长度为K时,关联矩阵(P
ij)也被称为K阶关联矩阵。
例1:考虑一个DNA序列s =
,它的1阶关联矩阵
图1所示。
3.2. 关键子序列
定义3(关键子序列):给定一个DNA序列s和它的一个关联矩阵(Pij)M×4,假如把关联矩阵的第j列对应的字符拼接在第i行对应的字符串之后就可以获得s的一个新的子序列,记为i∞j。设置一个最小关联阈值Min-Ass,当关联矩阵中的某个Pij ≥ Min-Ass时,那么利用i∞j操作得到的序列被称为s的一个关键子序列。特别地,假如i∞j的长度是K,那么该序列被称为s的一个长度为K的关键子序列。
例2:对于图1中的DNA序列和一阶关联矩阵,如果Min − Ass = 2,则我们可以找到长度为2的关键子序列:
,
,
,
,
,
和
。
定义4(最大关键模式):给定一个DNA序列s,它的一个关键子序列被称为一个最大关键子序列,

Figure 1. The first level association matrix of the DNA sequence s in Example 1
图1. 例1中DNA序列s的1阶关联矩阵
当且仅当它是关键子序列但不是其他关键子序列的真子串。
3.3. DNA序列中的关键子序列挖掘算法
事实上,在DNA序列中发现关键(子)序列模式是DNA分析的一个重要目标。利用关联矩阵结构,我们可以从较短的关键子序列中迭代生成较长的关键子序列。
例3:在例2的基础上,我们可以逐步得到2阶、3阶和4阶关联矩阵,如图2(a)、图2(b)和图2(c)所示。
综合例1到例3,对于例1给出的原始DNA序列,其挖掘关键子序列的挖掘过程归纳为:通过1阶关联矩阵,得到s的长度为2关键子序列集合是{
,
,
,
,
,
,
};由长度为2的关键子序列集合生成2阶的关联矩阵,进而得到长度为3的关键子序列集合是{
,
,
};由长度为3的关键子序列集合生成3阶的关联矩阵,进而得到长度为4的关键子序列集合是{
};显然,没有发现长度为5的关键子序列。此外,对应的最大关键子序列集合也可以被发现,即{
,
,
,
}。
基于例1到例3的解决问题的思路,利用长度递增的逐步迭代思想,算法AM给出了从一个DNA序列中发现关键子序列集合的过程描述。
4. 实验与分析
为了评估本文算法的有效性,我们从美国国家生物技术信息中心的网站(http://www.ncbi.nim.nih.gov)下载了实验数据集。该数据集来自于白细胞介素-6的DNA序列(简称IL-6),该数据集长度是12139。
实验是在一台4GB内存、使用英特尔酷睿i3、1.40 GHz处理器的计算机上进行的。采用的对比算法是目前引用率较高的序列挖掘算法GSP [6] 。实验的目标主要是检测本文算法的效率(包括时间效率和空
间效率)。
实验1:(不同的最小关联度下的执行时间)。利用IL-6数据集,分别设置最小关联度(对应原始GSP算法的最小支持度)为2%~10%,测试本文提出的AM算法和GSP算法的运行效率。图3给出了对应的实验结果。
图3表明:随着最小关联度(最小支持度)的增加,AM和GSP算法的执行时间都在下降。这是因为更大的最小关联度(最小支持度)意味着将生成更少的关键子序列。然而,AM算法在处理DNA序列时效率明显高于GSP算法。
实验2 (不同的最小关联度下的内存空间)。利用IL-6数据集,分别设置最小关联度(对应原始GSP算法的最小支持度)为2%~10%,测试本文提出的AM算法和GSP算法的内存使用情况。图4给出了对应的实验结果。
图4表明:随着最小关联度(最小支持度)的增加,AM和GSP算法的内存空间使用都在下降。这是因为更大最小关联度(最小支持度)意味着将生成更少的关键子序列。然而,AM算法在处理DNA序列时的空间占用明显优于GSP算法,尤其是在产生较多关键模式时。
实验3:(不同的DNA序列长度下的执行时间)。利用IP-6数据集,我们截取不同容量的DNA序列。考察在固定的最小关联度为5%时,AM与GSP算法的执行时间的攀升情况。图5给出了对应的实验结果。
 (a) (b) (c)
(a) (b) (c)
Figure 2. The 2nd, 3rd and 4th level association matrixes of the DNA sequence in Example 1
图2. 例1中DNA序列s的2阶、3阶和4阶关联矩阵
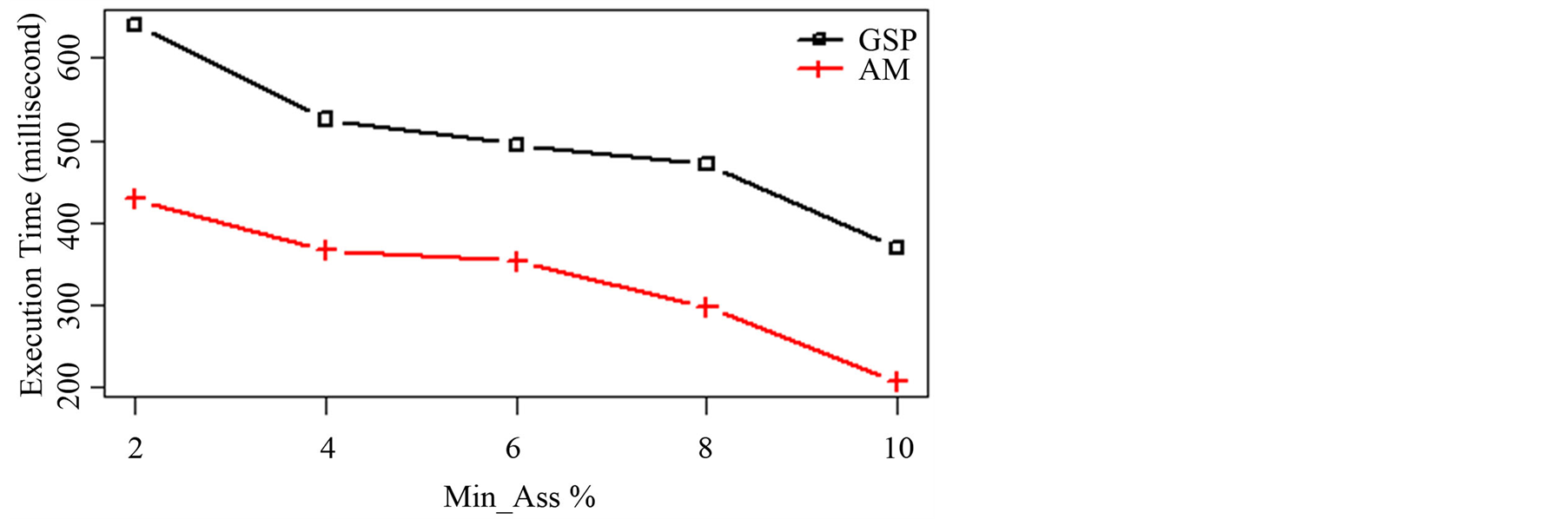
Figure 3. Curve: executing time changes of AM and GSP with increasing minimum association degrees
图3. 最小关联度增加时AM与GSP执行时间的比较

Figure 4. Curve: space changes of AM and GSP with increasing minimum association degrees
图4. 最小关联度增加时AM与GSP内存空间的比较

Figure 5. Curve: executing time changes of AM and GSP with increasing sizes of DNA sequences
图5. 随着DNA序列长度增加时AM与GSP执行时间的比较
图5表明:在固定的最小关联度(支持度)下,随着DNA序列长度的增加,AM和GSP算法的执行时间都会有所增加,但是它们都具有很好地可攀升性。当然,AM算法整体是优于GSP算法的。
5. 结论
本文针对DNA序列挖掘的特殊需求,设计了一个关联矩阵的数据结构。它的空间紧凑型使得它更适合用于挖掘“小项目集但大容量”的序列。毫无疑问,DNA序列属于这样类型的序列。然而,在现实世界中,这样的序列还有很多,如:生物信息学的蛋白质序列也仅有20个字母可以表示;随着时间变化的股票涨跌序列(可以只关心涨、平、跌3种状态)等。因此“小项目集但大容量的序列”是序列挖掘的一个具有很好研究和应用价值的分支。本文研究的问题和设计的方法只是其中的一部分,将来还有许多工作需要进一步探索。
基金项目
国家自然科学基金“基于数据分布评估和支持向量机方法的分布式数据流挖掘模型和算法研究”(No. 62173293)资助。