1. 引言
图像拼接是计算机视觉领域的一个重要分支。近年来为了解决大视野全景图和高分辨图片两种需求的矛盾，国内外对全景图拼接的研究上升到了一个新高度。但是，分析对壁画等数字保存的要求，无论是传统的图像拼接流程还是单应性投射模型，已经不适用壁画拼接的情况。
传统的单应性投射模型不考虑相机的视差，而为了获取壁画的每个细节，必须移动相机。由于壁画表面凹凸不平，幅面之大，分辨率之高都无法用传统的图像拼接流程来解决。
本课题根据基于特征值图像配准算法理论，按照图像拼接的一般流程，在图像预处理，图像特征值提取，全局调整等基础上进行多视点的全景图像拼接算法的研究。对如何获得相机内外参数的方法进行深入研究，探讨如何制定最佳全局约束，通过调整相机内外参数，三维重建特征点云拟合出最佳平面，创建合理的图片数量为框架以及调整非框架图片的投射顺序等多渠道来减小拼接过程中的累积误差，并借助图像处理平台设计实验，对拼接图像实验结果的准确性、实时性和有效性进行研究。
本文提出敦煌壁画全景图的新拼接流程，拟解决当前图像拼接的研究领域中存在的不足，在高精度，大幅面的全景图拼接配准流程方面进行创新。
2. 图像拼接相关工作
2.1. 基于特征值的图像配准技术
图像配准技术是全景图拼接成功的关键之一，目前主要的图像配准方法有直接匹配和基于特征值的匹配。前者又叫基于空间像素灰度值拼接技术。基于特征的配准方法能够容忍更大的图像差异，有助于获取稳定的配准结果[1] 。由于所提取的特征点个数一般远小于图像中的像素数，在快配准过程的运算速度具有计算量小、速度快的特点，同时对于图像的畸变、噪声、遮挡等具有一定的鲁棒性等优点。
这些特征提取算法的优异性能，使得基于特征的图像配准成为当前的主流选择。Lowe [2] 提出的SIFT特征子与Bay [3] 提出的SURF特征子是现今最常用的特征子。
本文所采用的特征子配准方法是基于Lowe提出SIFT (Scale-invariant feature transform)算法得到的特征点，该算法实质是在不同的尺度空间上查找特征点及其方向。由于SIFT特征具有尺度不变性，即使同一物体处于两个不同的尺度的图像中或者图像经过投射，光照等变化后，我们仍可以通过提取图像的SIFT特征而匹配成功。课题下文所描述的特征点特指SIFT特征子经过RANSAC算法后所得内点 [4] 。
2.2. 基于SFM流程的三维重建
传统的图像拼接投射矩阵仅仅考虑相机的纯旋转运动 [4] ，其基本假设为相机之间不存在视差。图像配准过程中，人们一直优化单应性投射矩阵，得到相对准确的投射矩阵来消除相机的移动所带来的误差。当相机发生位移变化时，传统的拼接算法并不能很好地达成预期目标。Agarwala等提出利用三维重建恢复拍摄物体的三维位置信息运用到图像拼接中 [5] 。
SFM，全称为structure from motion [4] ，从运动中恢复结构，现广泛应用于三维结构的重建以及获得相机位置姿态方面。
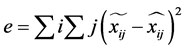(1)
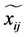表示预测的二维点坐标，
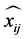表示测量得到的二维点坐标。在优化到两者之间最小误差代价时，我们可以得到特征点的三维信息以及相机的内外参数。多视图的三维重建是先对摄像机进行标定，计算出摄像机的图像坐标系与世界坐标系的关系。利用多个二维图像中的信息重建出三维信息。采用BA (Bundle Adjustment) [6] 技术，减少观测图像的点和参考图像(预测图像)的点之间位置投影变换(重投影)误差e。三维重建的结果并不能直接改善图像拼接的效果，尽管如此，仍有不少将其使用于图像拼接领域的成功尝试。
沈武魁 [7] 采用SFM算法，利用图片之间的二维点估算出特征点的三维坐标，拟合出一个代价最小的最佳投影平面，将所有图片正射投影到该平面，构建全景图，并在后续工作中尽可能的减少了由于三角剖分导致的边缘内容损失。
徐玉华分别对于已知和未知相机位姿的情况，提出拼接策略 [8] 。对于相机位姿未知的情况，先采用 SFM方法恢复相机姿态和场景稀疏结构信息，再进行全局稀疏优化图像变换参数，进行近似平面场景的多视图图像拼接研究。
2.3. 多重单应模型APAP投射
为了优化单应性投射模型，现今已有多重单应模型被提出以减少由单应投射产生的拼接误差。Gao [9] 等提出双单应性模型，用以投射具有两个主要平面的场景。这一模型由两个单应模型的加权线性组合构成，其中的权重随着空间位置变化而不同。Lin等 [10] 提出了smoothly varying affine模型，用以投射全局仿射变化的场景，同时允许局部形变。Julio Zaragoza等 [11] 提出的APAP (As-Projective-As-Possible)拼接，在保存了被摄体的整体单应性假设的前提下，假设被摄体的细节部分满足不同的局部单应性，并通过一个新的滑动窗口方法，被称为Moving DLT (Moving Direct Linear Transformation)，对其进行加权估计，其拓展了之前Gao等 [9] 对一张图像计算两个单应性矩阵的尝试，在很大程度上解决了单应性拼接方法中，噪音和视差带来的图像错位和鬼影。
在直接线性变换(DLT)算法基础上确定投射矩阵H，记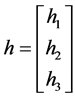
，h矩阵只有前两行线性相关，记
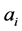为前两行。
优化目标是
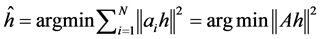(2)
约束
。
(3)
像素点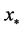
与第i个特征点呈几何距离相关。对
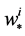进行规格化得到
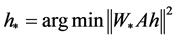(4)
其中
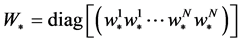(5)
对每一个像素点进行APAP投射，计算成本较高，且没有必要。将图片分成若干块，每一块的中心像素点采用APAP算法进行投射，能降低时间复杂度。
3. 基于预定位图片框架策略的算法
为了避免累积误差带来的全景图变形，消除在拍摄壁画时，平移相机所带来的影响位置变化，这里采用SFM算法恢复相对准确的壁画场景。模拟三维重建后，用最小二乘法拟合最佳平面，将所有的特征点进行正射投影到该平面。从中选取部分图片作为初始位置，作为全景图的全局约束，不再参与全局调整。其他非框架图片根据预定位的图片进行APAP单应性投射。图片的配准流程如图1所示。
3.1. 特征点的三维重建
本课题采用Visual SFM软件经过SFM流程得到稀疏的特征点云，根据最小二乘法，我们拟合一个最佳平面，将所有的特征点正射投影到该平面，这个过程中完成将三维点到平面二维点的转化。
3.2. 拼接系统的框架图片确定
在经过SFM流程处理后，我们将每一幅图片映射到三维场景中，除了得到粗略的相机位置信息，同时也得到每一幅图片的特征点信息。由于所有图片都处在一幅全景图中，图片与图片之间存在重合信息，由这些重合信息来确定匹配的特征点。通过SFM流程，我们观察到一些特征点同时出现在若干张图片中，同一对匹配特征点出现在不同图片中的数量也尽不同。
3.3. 非框架图片进行全景图投射的顺序
如图2所示，当一张图片B投射到位置准确的图片A (预定位的图片)时，与之有重合部分的A特征点Pab1位置是准确的，而另一些没有重合的像素点Pb2 (黄色框)的投射矩阵H是根据重合部分Pab1计算得来，并非实际的投射计算的H进行变换，由此可知，这些像素点投射后的在全景图中的位置与实际的位置有偏差，反映在全景图中Pb2是不确定的，当另一张图片C与B图片的Pb2有匹配点Pb2c，将C的进行单应性投射时，由于投射的基础Pb2是不确定的，那么图片C的位置反映在全景图的是不准确的。
Figure 1. Image stitching using invariant features
图1. 基于特征点配准流程示意图
Figure 2. Registration error caused by uncertain images location
图2. 不确定的图片引起的配准错误示意图
尽管APAP投射的方法能提高局部投射的准确性，但是若投射的基础不对，也只是在投射基础不正确的前提下，配准出错的更少一点而已。以此类推，误差累积更甚。非框架图片的即使并没有与周围框架图片有匹配点，为了尽量准确的投射到全景图中，放入框架图片投射的顺序也至关重要，拟定的策略按照SFM重建后与框架图片匹配的特征子的数量从大到小以此投射至全景图中。
综上问题所在，拼接算法的策略：
1) 选取三维重建的特征点，在重构中，给定其中两幅视图的一组点对应，该点在第三幅视图上的位置就可以确定，三视图比两视图的3个自由度点多提供2个测量，而且景物直线的解是超定的，可以通过对测量误差适当的最小化来估计 [12] 。
2) 为了尽量重现真实三维情况，框架图片选取包含重建特征点最多的图片，计算每一张图片在三维重建中包含的特征点，从高到低进行排序。
3) 选取框架图片策略：尽量减少框架图片之间重叠，尽量包含更多的重建的可靠的三维点。
4) 建立框架后，按照图片顺序放入框架内，为了尽量将非框架图片植入准确的位置，计算每一张图与周围的框架图片有重叠张数的数量，按照其数量从高到低进行排列，依次与框架进行拼接。若出现非框架图片与接壤的框架图片数量一致时，则比较匹配点的对数取大者。
判断框架选取的策略评判定为粗拼接阶段为三维重建特征点数量，和拼接完成后全景图的均方误差作为评价拼接质量的定量指标。
具体算法思路如表1所示。
4. 实验结果
拼接之后的图像质量评价(IQA)主要分为主观和客观两种评价方法 [13] ，主观评价基于人的视觉主观评判，达到视觉可接受的范围即可，由于人的主观带有不确定性以及工作量巨大而往往导致评判不准确。对于图像的客观质量评价，从参考源的角度可分为全参考FR (Full-reference)，无参考NR (No-reference)，弱参考RR (Reduced-reference)。目前主流的评价方法是全参考方法 [14] ，拼接模型普遍使用RMSE，即均方误差作为评价拼接质量的定量指标。
对于估计变化矩阵f和对于匹配的特征点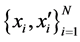
，均方误差RMSE计算经过f投射变化后平均像素差 [11] 。
(6)
主流商业图像拼接软件如AutoPano Giga，Photoscan等，RMSE < 3即被认为是拼接质量优异。用敦煌壁画56样张进行实验，本课题算法结果如下(只考虑图像配准，未进行全局BA调整，图像只进行简单的线性融合)。
根据设计的框架图片选取策略，实验生成的框架图如图3所示。
不考虑图像放入顺序的实验结果如图4所示。
可以很明显观察到中间一排最右侧的佛像畸变严重，分析原因可发现该图像进行投射时，与之匹配的特征点均为非框架图像，不确定的匹配点位置导致匹配信息不够。同理，左下侧红色框框内佛像拼接处出现断裂。
改进非框架图片的投射顺序，考虑图像放入顺序的实验结果如图5所示。
很明显，从主观视觉上判定，实验一中的佛像畸变和出现的鬼影都消失了，最底下一排的佛像也未出现断裂的情况。拼接效果大幅度提高。
客观定量分析，三维重建后框架中包含的特征点数量54,605，框架中图片张数13。总误差e由公式(1)计算所得，两组实验结果数据包括总误差，内点数量以及重要评判指标RMSE，如表2所示。
为了得到更清楚的对比效果，选择主流商用软件拼接结果作比较，可以看出，本实验课题算法在大幅面，高精度的壁画拼接上更为出色。图6为Photoscan所拼接的56张敦煌佛像全景图，由于该软件良好的融合算法弥足了图像拼接过程中匹配不准，从整体来看，佛像畸变严重，长宽像素比失调。图7为AutoPano Giga同一资源拼接的全景图，拼接结果透视效果严重，导致整个投射面严重畸形。
表1. 算法步骤表
Table 2. Evaluation for two simulations
表2. 两组实验定量分析结果表
Figure 3. Image framework using located in advance
图3. 预定位图片的框架示意图
Figure 4. No-frame images project at random
图4. 随机选取非框架图片进行投射实验结果图
Figure 5. No-frame images project in order
图5. 考虑非框架图片投射顺序实验结果图
Figure 6. Panorama stitching with Photoscan
图6. Photoscan软件拼接效果图
Figure 7. Panorama stitching with KolorAutopano Giga
图7. KolorAutopano Giga软件拼接效果图
5. 结束语
本文在图像拼接的配准流程中进行研究分析和优化，采用SFM三维建模模拟壁画的场景，恢复特征点云，拟合投射到一个最佳平面，合理选出部分图像作为框架，自动化完成框架图片的选取，生成最优框架，其他图片进行多重单应性投射。既保证了壁画的全局约束，同时在保证了非框架图片在投射过程中全局调整的灵活，最后，与主流的商业全景图拼接软件作对比，效果更为出色。
尽管本文算法效果与之前相比，有了较大的提升，但由于壁画精度较高，在细节方面还有待提升。改进策略如下：
1) 对非框架图片进行全局Bundle Adjustment调整，进一步优化匹配误差。
2) 改进本课题图像拼接融合过程中简单的线性融合方法，利用图像融合技术正确消除拼接缝，图像扭曲，重影模糊等，对光照增益补偿。能正确完成基于“预定位图像”策略的多视图全景图的拼接。