1. 引言
爆轰与人类生产生活的很多方面密切相关，然而目前对于爆轰问题的研究还很不成熟，对于爆轰的机理认识还不够清楚[1] [2] 。爆轰过程中涉及到多重的物理相互作用、非平衡化学和传输过程等特性，是一个非常复杂的反应流动过程，对于爆轰问题的研究目前主要的方法是数值模拟[3] -[5] 。传统的宏观流体力学方程，是基于连续介质假设和局域平衡态假设的，在研究系统的非平衡过程中过于粗糙。近20年以来兴起的Lattice Boltzmann方法(LBM)，可以看作是Boltzmann方程的特殊离散化，在流动问题研究方面获得广泛应用[6] -[8] 。近年来许爱国课题组将其进一步发展为复杂流体系统的一种微介观动理学建模，为系统内非平衡行为的描述、非平衡信息的提取、非平衡程度的度量提供了一种简洁、有效的方法；从而反过来促进了非平衡统计物理学基本描述方法的发展。这个新的思路已在燃烧与爆轰、多相流、流体不稳定性等方面获得推广与应用，获得了一些传统流体模型所不便描述的新的认识[9] -[17] 。
本文基于本课题组的建模思路[9] -[11] ，在文献[14] 提出的高速可压LBGK模型的基础上构建了一个新的爆轰离散Boltzmann模型(DBM)。为了方便研究化学反应速率对爆轰特性的影响，模型中采用了新的化学反应率模型。基于以上模型，考察了不同反应速率情形下的爆轰波特性。对比不同反应速率情形下，爆轰波结构的差异，找出爆轰波不出现von-Neumann峰值的临界反应速率，并考察了临界反应速率两侧的爆轰特性，研究结果有助于对反应速率对爆轰波结构的影响的进一步理解。
2. 模型简介
2.1. DBM模型
在文献[14] 给出的LBGK模型的基础上添加化学反应的作用便得到本文所采用的DBM演化方程，如下式所示：
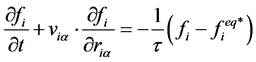(1)
式中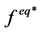
为加入化学反应作用后求得的局域平衡态分布函数。
离散速度模型采用如图1所示的16离散速度模型：
16个离散速度的二维坐标分量为：
符号cyc：代表循环置换，例如
即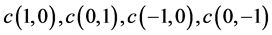
。c代表离散速度的取值，c值的大小需根据模拟的问题合理调节，在本文的模拟中取c = 3。
2.2. 化学反应率模型
一个合适的化学反应率模型，对于爆轰问题的模拟至关重要[2] [16] 。1980年Lee-Tarver提出了Lee-Tarver反应率函数，也称为点火成长模型。该模型由点火和成长两项组成，第一项描述热点的形成，第二项描述反应的增长[1] 。其形式为：
(2)
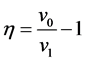(3)
式中
表示反应进程变量；
和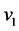
分别表示反应前后炸药比体积，
表示未反应炸药的相对压缩度；
Figure 1. Schematic of the discrete velocity model
图1. 离散速度模型
均为常数。
事实上，有时候为了研究问题方便，可以对上述模型进行简化。如果研究的问题主要关心反应的成长过程，可以只取式(2)的第二项，即
(4)
在式(4)若取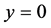
，就得到Miller能量释放模型的形式[18] 。本文要研究反应速率对爆轰波结构的影响，为了方便分析反应速率的变化也只取式(2)中的第二项；作为初步研究，先考虑一种简单情况，在式(4)中取
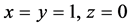。另外，考虑到热起爆的起爆条件，便得到本文所采用的化学反应率模型，如下式所示：
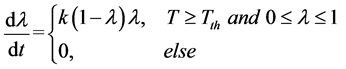(5)
式中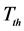
表示起爆温度，k即相当于式(4)中的
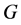，表示爆轰成长项的系数，也可以类比Arrhenius模型的形式称之为反应速率常数[19] [20] 。
本文中，我们考虑最简单的反应情形：一种反应物，一种生成物，且反应前后物质的量不发生变化。
可用
表示反应物的物质的量浓度，
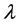表示生成物的物质的量浓度，考虑反应不可逆的情形，反应开始时刻
，反应结束时刻
。
3. 模型验证
在这一部分，首先通过一些经典算例来验证模型的可靠性。对于方程(1)数值求解，时间微分项采用一阶向前差分求解，空间微分项采用数值稳定性较好的NND差分格式求解[21] 。
3.1. Colella爆炸冲击波问题
模拟区域网格数为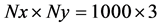
，网格宽度为
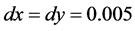，时间步长为
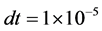，弛豫时间为
，比热比为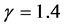
。对于方程边界值采用差值外推的方法确定，初始条件设置为：
把模拟区域从中间进行分割，下标为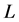
表示左半区域的初始值，下标为
表示右半区域的初始值。该算例可用于测试新构建的DBM的健壮性和数值精度。
图2给出了
时刻的密度、温度、速度和压力在x方向上的空间分布。通过与解析解的对比可以看出，新构建的DBM具有较强的捕捉激波的能力，对于模拟爆炸冲击波问题具有较好的稳定性和较高的精度。
3.2. 自持稳定爆轰问题
考虑一充满预混可燃气体的爆轰管，左端初始值设置为CJ爆轰波后的理论值。如果化学反应速率选取合适，化学反应释放的化学能刚好可以提供爆轰波向前传播所需的能量，则可以得到一个自持稳定传播的爆轰波[2] 。
模拟区域网格数为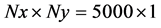
，网格宽度为
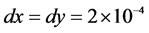，时间步长设置为
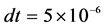，弛豫时间为
。另外，关于化学反应参数的取值，单位质量的反应物完全反应释放能量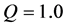
，起爆温度
，反应速率常数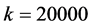
。初始状态设置如下：
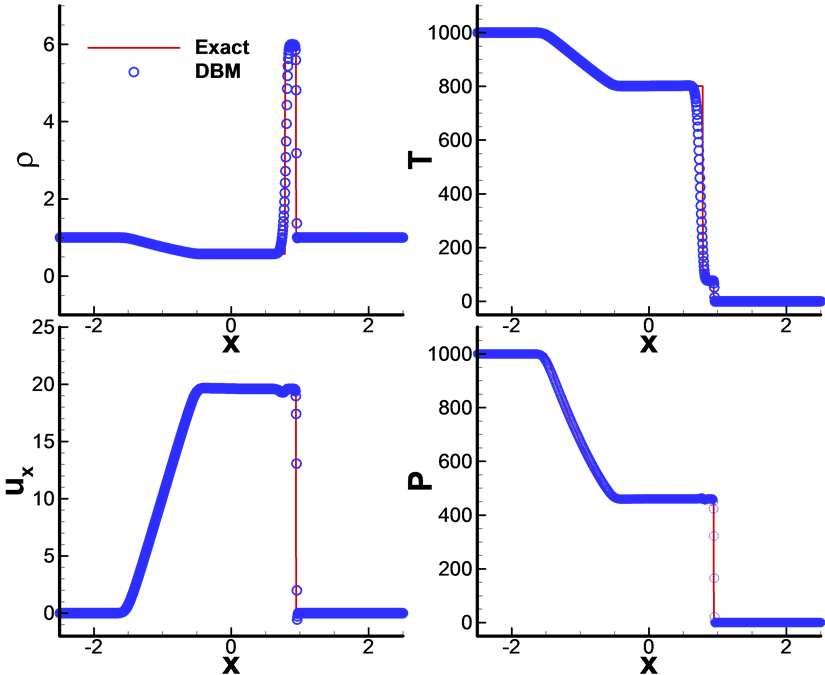
Figure 2. Comparisons between DBM result and the exact solutions for Colella’s explosion wave test at the time t = 0.04
图2. t = 0.04时刻Colella爆炸冲击波算例的DBM模拟结果与解析解对比图
将模拟区域从
处分割成左右两部分，下标L代表左边区域的初始状态，下标R代表右边区域的初始状态。该算例具有精确的CJ理论解，可以通过该算例检验加入化学反应作用后模型的可靠性和模拟精度。
图3和图4给出了DBM模拟结果和CJ理论值的对比，从图3中可以看出，爆轰波前后的宏观物理量的空间分布，DBM模拟结果与理论解符合较好。从图4可以看出，爆轰过程中反应进程和爆轰波速的模拟结果与理论解也符合较好。说明新构建的爆轰DBM具有较高的模拟精度。
4. 模拟结果及分析
为了考察不同反应速率对爆轰波结构的影响，采用与3.2中相同的模拟条件，分别模拟了几种不同反应速率条件下的爆轰情形。图5(a)中可以直观的看出，反应速率较小时，爆轰波会有明显的von-Neumann峰。随着反应速率的大幅增加，爆轰波的峰值会逐渐降低。当反应速率达到某一临界值时，爆轰波的von-Neumann峰值消失，这一反应速率称为临界反应速率，记为
。在临界反应速率附近，爆轰波的压力分布与CJ理论解几乎完全符合。达到临界反应速率之后，如果反应速率继续增加，爆轰波的波阵面以高于CJ爆轰的波速向前传播，此时得到的波后稳态对应弱爆轰状态。针对本文中的反应率模型，
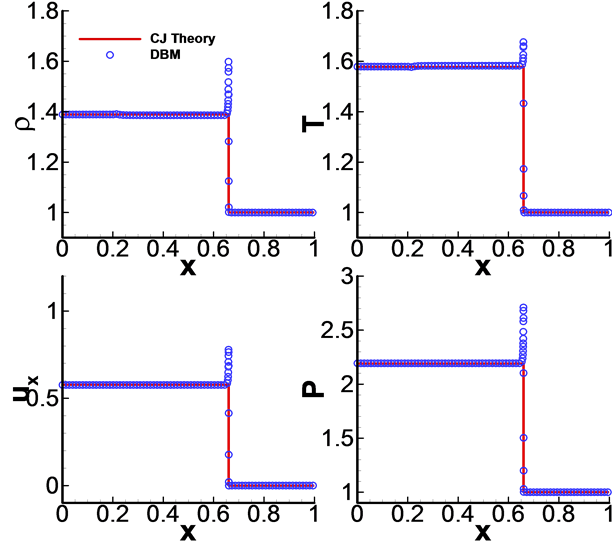
Figure 3. Comparisons between DBM result and the CJ theoretical solutions for self sustaining detonation test at the time t = 0.03 (density, temperature, velocity and pressure behind the detonation)
图3. t = 0.03时刻自持爆轰波DBM模拟结果与CJ理论解对比图(波后的密度、温度、速度和压强)
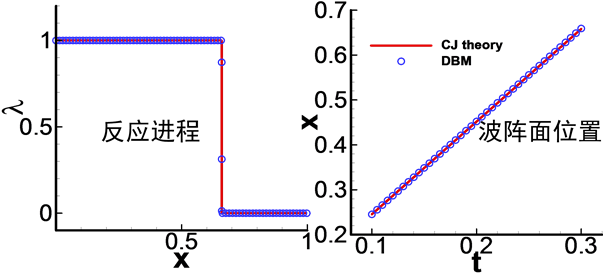
Figure 4. Comparisons between DBM result and the CJ theoretical solutions for self sustaining detonation test at the time t = 0.03 (reaction process and the wave velocity)
图4. t = 0.03时刻自持爆轰波DBM模拟结果与CJ理论解对比图(反应进程与波速)
通过多次调整反应速率常数模拟发现，临界反应速率对应的反应速率常数近似取值为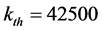
。
一般来说，CJ理论解是基于以下两个假设：爆轰波阵面宽度无限窄和化学反应速率无限快。而事实上，对于数值模拟和实际的情况，爆轰波波阵面不会无限窄，反应速率也不会无限快，这样稳定状态的爆轰就不一定刚好是CJ爆轰。通过本文的模拟发现，当化学反应速率选取比较合适，使得刚好在有限的波阵面宽度里完成化学反应，这种情形下，可以得到与CJ理论完全一致的结果。这一反应速率即是临界反应速率。
Figure 5. Pressure profiles and phase diagram of pressure and specific density at different reaction rates
图5. 不同反应速率情形下的压力空间分布和P-v相图
从图5(b)的P-v相图中也可以看出，当反应速率小于临界反应速率时，爆轰过程是先沿
附近的雨贡纽线冲击压缩，这一过程可近似认为没有化学反应的发生，反应物的压力和密度等参数急剧上升，甚至远远高于稳定状态对应的值，当达到某一最大值(即von-Neumann峰值)后，再逐步向
的雨贡纽线上的稳定状态点过渡，由于强爆轰相对于波后介质是亚声速运动，边界处的扰动最终会追赶上爆轰波，因此强爆轰不能形成，最终的稳定状态只能是图中的CJ点。
当反应速率等于临界反应速率时，在预压冲击过程就已经有了明显的化学反应作用，而当冲击过程结束时，化学反应也完成了，因此反应物的状态从达到起爆温度开始就从
向
的状态过渡，压力和密度等参数没有先上升后下降的过程，而是逐渐的增加到最终状态即CJ状态。
而对于反应速率大于临界反应速率时，预压冲击过程就已经开始了化学反应，并在理论的冲击过程结束之前完成反应。这种情形下的爆轰波以大于CJ爆轰波速的速度快速向前传播，反应物的状态一旦达到起爆条件就快速从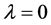
向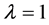
的状态过渡，并很快达到曲线
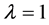上的弱爆轰状态。由于弱爆轰的波阵面相对于波后介质是超声速运动，后面的扰动不能追赶上来，因此弱爆轰状态可以维持，这种情形下爆轰反应区域的宏观物理量变化过程与临界反应速率情形类似，只是最终状态是弱爆轰状态，相比于CJ爆轰状态弱爆轰状态下的压力和密度更小，爆轰波速更大。
5. 结论
爆轰波的经典CJ理论是基于两个假设的：爆轰波波阵面无限窄和化学反应速率无限快。而事实上，这两个假设在实际中是无法满足的。通过本文的模拟发现，当反应速率取为某一特定值时，会得到与CJ理论完全一致的爆轰波结构，这一反应速率定义为临界反应速率。本文针对文中所采用的具体化学反应率模型，通过多次模拟找到了一个近似的临界反应速率对应的反应速率常数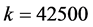
，并分析了化学反应速率取值为临界反应速率两侧时，爆轰波波结构的差异。当反应速率小于临界值时，爆轰波结构中会出现von-Neumann峰值点，反应区域的压力、密度参数先在
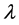变化较小的区域内上升至von-Neumann峰值，然后过渡到
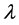=1对应的反应完成状态，系统最终的状态是CJ爆轰状态。而当反应速率大于临界值时，波结构中不出现von-Neumann峰值，在系统温度达到起爆温度很短的时间内就有了明显的化学反应，反应区域的压力、密度参数直接向
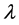=1对应的反应完成状态过渡，系统的最终状态对应弱爆轰状态。当反应速率处于临界值时，同反应速率小于临界值情形的过渡过程类似，系统最终状态刚好对应CJ爆轰状态。
基金项目
本工作得到计算物理重点实验室基金、国家自然科学基金(批准号: 11475028, 11202003)、理论物理国家重点实验室(中国科学院理论物理研究所) 开放课题(批准号: Y4KF151CJ1) 和爆炸科学与技术国家重点实验室(北京理工大学) 开放课题(批准号: KFJJ14-1M) 资助。感谢林传栋、甘延标、赖惠林在本文模型构建和文章写作过程中给与的讨论和帮助。