1. 引言
伪卫星定位系统通常具有抗干扰能力强、组网灵活和经济性好等优势，是实现北斗、GPS、GLONASS等全球导航卫星系统定位性能增强的主要技术手段之一。同时，伪卫星独立组网还可提供在全球导航卫星系统无法正常工作区域的导航定位服务，扩大其应用范围 [1] 。伪卫星定位技术一直是卫星导航领域研究的热点问题之一。
最初的伪卫星主要设置在地面上，用来测试或增强导航卫星系统。近几年，随着伪卫星技术的发展，伪卫星还被安装在飞机或高空飞艇上形成空中伪卫星，大大扩展了伪卫星的应用范围。
卫星导航和伪卫星都是基于测距的导航定位系统，其观测方程是典型的非线性模型。目前工程实践中最常用的定位方法是先将非线性的观测方程线性化，然后在设定初始位置的基础上进行迭代定位 [2] 。对于GPS卫星而言，由于卫星和接收机相距较远，通常认为从用户实际位置到卫星的视线平行于从用户估计点到卫星的视线，观测方程的线性化误差可以忽略不计 [3] 。但是，在伪卫星定位系统中，由于伪卫星与接收机相距很近，用户估计点位置与真实位置到伪卫星视线间的夹角较大，由此引起的线性化误差将显著变大，因此，在伪卫星定位解算中必须有效地评估线性化误差对定位估计带来的影响。
有关非线性误差对定位影响的分析，国内外研究相对较少。针对非线性问题理论，Teunissen提出了三种测量非线性的简单方法，给出了以Hessian矩阵最大最小特征值表示的线性化残余误差的边界估计 [4] 。孟键、王金岭、高为广等基于上述方法，分析了GPS和伪卫星的非线性变换所带来的误差情况，但尚未开展评估方面的研究 [5] - [8] 。万晓光等从卫星与用户之间的几何关系出发给出了线性化误差的边界值，并提出了一种评估线性化误差的具体方法 [3] 。该方法根据影响非线性最小二乘法收敛情况的几个因素，即观测方程的非线性强度、观测值的精度以及观测方程的特性，给出了判断非线性最小二乘法是否局部收敛的条件。
在此基础上，本文针对空中伪卫星，充分考虑了不同伪卫星观测量对定位解算贡献的差异，提出了一种基于高度角的伪卫星定位线性化误差评估的判定准则，满足该判定条件，则最小二乘法必收敛，否则不一定收敛。并用仿真数据对此方法的有效性进行了验证。
2. 线性化误差评估方法
在仅考虑用户位置为待估参数的情况下，伪卫星定位观测方程的线性化表达式为 [9] [10] ：
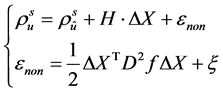(1)
其中，
表示用户到伪卫星的伪距；
表示用户到伪卫星的近似伪距；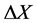
表示用户真实位置
与近似位置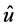
之间的距离，
，
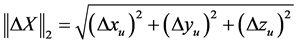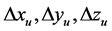分别表示用户真实位置与近似位置在
三个方向上的距离差；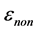
表示泰勒级数展开时的二阶及以上的项，
表示二阶以上的项；
表示二阶偏导矩阵。
残差函数可表示为
，
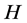即为
的Jacobi矩阵：
(2)
另外，由卫星和用户的几何关系还可得到线性化误差
的表达式为 [3] ：
(3)
其中，
表示用户真实点
与估计点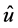
到伪卫星的这两条视线所构成的夹角，
。
当
时，
为极大值，即：
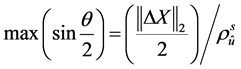(4)
这时，线性化误差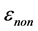
的最大边界值为 [8] ：
(5)
由式(5)可以看出，伪卫星的线性化误差取决于两个参数：位置近似的准确度
和伪卫星与用户间的距离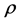
。基于这个结论，可给出一种检验线性化误差对于定位是否可以容忍的方法 [3] ，表达式为：
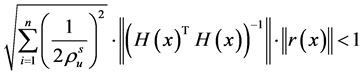(6)
其中，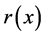
表示残差函数；
表示观测方程的一阶偏导矩阵；
是利用式(5)线性化误差的边界值结论以及
估计出的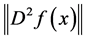
的最大值。
从式(6)中可以看到，不同伪卫星观测值被认为是等权的，此法虽然处理简单，但与观测值的实际不符，这样可能会对复杂的数据噪声过于简单化，使得最小二乘解失去它的最小方差性质，导致不合理的定位结果。但是实际中，伪卫星的高度角过低时，仰角小的卫星收到大气影响较大，信噪比较低，天线增益较小，同时易产生多径效应。因此，不同高度角的伪卫星观测值的精度通常具有较大的差异。如果忽略此差异，就会使最小二乘解失去其最优化特性，极有可能导致判定结果与实际不符 [11] 。针对此，本文拟引入与高度角相关的权函数用以改进上述线性化误差评估的方法，权矩阵的构建方式如下：
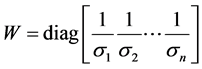
其中，方差
采用正弦函数模型进行表示，即
。
因此，改进之后的评估公式为：
(7)
当式(7)所示的条件满足时，采用最小二乘高斯-牛顿法迭代结果一定会收敛，实现定位解算。当不满足式(7)的条件时，高斯–牛顿法的迭代结果不一定收敛，为了保证系统的可靠性，需要进一步考虑采用其他定位算法实现定位。
综合此方法，对现有伪卫星定位流程进行如图1所示的改进，其中虚线框内是线性化误差的评估方法。
3. 仿真实验
3.1. 不同高度卫星线性化误差大小分析
通过第1节对线性化误差的定量分析可知，在
的条件下，可以得到线性化误差
的边界值，它仅与测站坐标误差和用户到卫星的距离有关。为比较线性化误差对GPS和伪卫星的影响，本文拟定距离用户20,000 km的全球导航卫星和距离用户200 m的伪卫星，分析其线性化误差随测站坐标误差的变化情况，如图2和图3所示，分别给出了线性化误差对GPS和伪卫星系统的影响的仿真结果。
Figure 1. The flow chart of pseudolite positioning
图1. 伪卫星定位流程图
Figure 2. The linearization error of GPS
图2. GPS的线性化误差
Figure 3. The linearization error of pseudolite
图3. 伪卫星的线性化误差
从上图可以看出：距离用户20,000 km的全球导航卫星，在测站坐标误差为200 m时，其观测方程线性化的最大误差仅1 mm；而距离用户200 m的伪卫星，在测站坐标误差为20 m时，线性化最大误差为1 m。
结合公式(5)分析，线性误差的边界值与用户到卫星的距离呈反相关，而与测站坐标误差呈正相关。由于GPS距离用户很远，伪卫星距离用户较近，线性化误差对GPS的影响很小，可以忽略不计，而对伪卫星系统的影响则很大，必须考虑其对定位的影响。
3.2. 线性化误差评估方法性能分析
为了充分验证本文提出的基于高度角加权的伪卫星定位的线性化误差评估方法对定位的改善，拟定了四种不同的伪卫星布网方案 [12] - [14] ，如图4~6所示，具体组网见表1。
基于上述不同的组网方案，现仿真生成伪卫星观测量，卫星与用户的钟差暂不考虑，测量噪声假设为与高度角相关的随机噪声，用高斯牛顿法进行100次的定位运算。
表2给出了在不同的布局方案与不同的伪卫星高度下，根据本文提出的基于高度角加权的伪卫星定位的线性化误差评估方法和传统评估方法计算得到的判定值，从中可以看到，当权矩阵为单位矩阵I时，3个方案都满足判定条件，而当权矩阵为高度角加权矩阵W时，正方形结构和四面体结构均满足判定条件，而四颗星的结构不满足。
Table 1. The comparison of three different pseudolite layouts
表1. 伪卫星三种不同布局方案对比
Table 2. The calculating values of three different pseudolite layouts
表2. 三种不同伪卫星布局方案的判定值解算
根据图1所示的伪卫星定位解算流程图，对20 km高度的伪卫星进行定位解算，结果如图7~9所示：
由表3可以看出，正方形结构和四面体结构求解出的用户位置误差分别为4.50和5.68，而四颗星的结构求解出的用户的定位误差为21.66，明显较大。
综上所述，四颗星结构的定位误差较大，高度角加权时，其判定值不满足判定条件，符合预期的结果；而权矩阵取单位阵时，四颗星结构满足判定条件，与预期的结果不符。由此可知，基于高度角加权的线性误差评估方法，可使评估的结果更为准确。
由于空中伪卫星被应用于气球或高空飞艇上，高度变化比较灵活，为了更充分验证本文提出的基于高度角加权的伪卫星定位的线性化误差评估方法的适用性，探讨在不同的伪卫星高度下，用户的定位误差对比分析。图9~11是对四颗星结构在伪卫星高度为5 km~20 km时用户的定位误差。
由表4可以看出，四颗星结构中不同高度的伪卫星定位误差均很大。结合表2的判定结果，在四颗
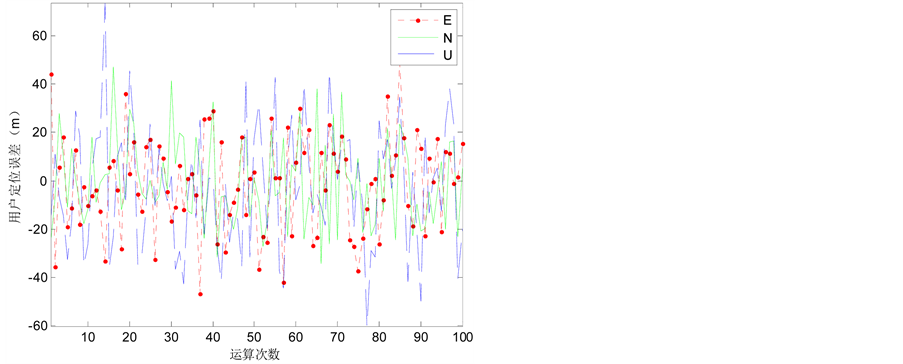
Figure 7. The positioning errors of square structure—20 km
图7. 正方形结构定位误差(20 km)
Figure 8. The positioning errors of tetrahedron structure—20 km
图8. 四面体结构定位误差(20 km)
Figure 9. The positioning errors of four pseudolites—20 km
图9. 四颗星的定位误差(20 km)
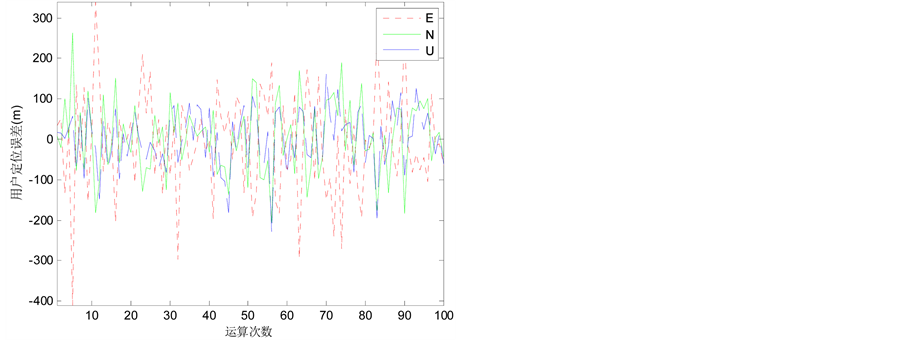
Figure 10. The positioning errors of the height of 10 km—four pseudolites
图10. 高度10 km定位误差(四颗星)
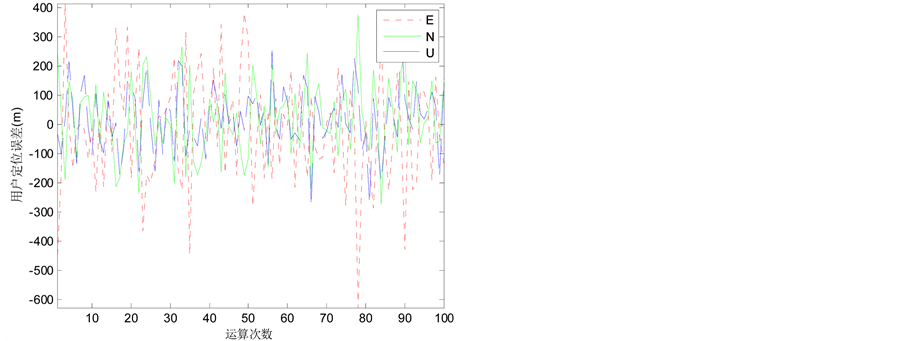
Figure 11. The positioning errors of the height of 5 km—four pseudolites
图11. 高度5 km定位误差(四颗星)
Table 3. The positioning errors of three different pseudolite layouts
表3. 三种不同的伪卫星布局方案的定位误差统计
Table 4. The positioning errors of four pseudolites of different heights
表4. 四颗星结构不同伪卫星高度的定位误差统计
星结构中，不同高度下，高度角加权时，其判定值均不满足判定条件，符合预期结果；而权矩阵取单位阵时，均满足判定条件，与预期的结果不符。由此可知，基于高度角加权的伪卫星定位线性化误差评估方法，适用于不同高度的伪卫星定位。
4. 结束语
由于伪卫星距离用户较近，模型线性化时产生的误差通常不能忽略，本文提出了一种基于高度角加权的伪卫星定位线性误差的评估方法，以判断下一步是否可以使用最小二乘迭代法进行定位解算。主要结论如下：
1) 伪卫星距离用户较近，线性化误差较大，因此，在伪卫星系统中，必须考虑线性化误差对定位的影响。
2) 线性误差判定条件中的权矩阵用卫星高度角定权法表示时，比用等权策略的判定结果更为准确。
3) 不同的伪卫星星座，线性化误差也不同。满足线性误差评估的判定条件时，定位误差较小，反之则定位误差较大。
另外，此方法还可应用到选星上，基于线性误差评估的结果，改善用于定位的伪卫星的组网布局，从而得到更好的定位结果。
致谢
课题编号：2015AA124101-03。国家高技术研究发展计划(863计划)课题：“基于新一代通信网络的室内定位导航新技术”。
课题编号：2015AA124002。课题名称：低成本GNSS/INS深耦合大众车载导航终端与应用示范。