1. 引言
非线性积分微分方程在许多科学领域有着广泛的应用,因此引起了众多学者的广泛研究,例如物理中的在多孔催化剂颗作用下的传热和传质参见文献[1] ,生物中细胞中的氧扩散 [2] 等,其中,带有初边值条件的积分微分方程更是学者研究非线性积分微分方程的热点之一,参见文献 [3] [4] 。
在本文中我们将运用RKM和ADM分解方法相结合来求解下面的带有边值条件的积分微分方程,如下
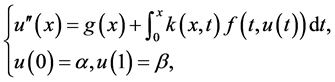 (1.1)
(1.1)
其中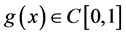 ,
, ,
, ,并且
,并且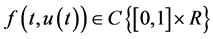 是非线性项,且满足Lipschitz 条件,即存在常数
是非线性项,且满足Lipschitz 条件,即存在常数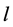 ,使得
,使得
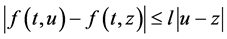 。 (1.2)
。 (1.2)
方程(1.1)也可以通过齐次化过程改写为
 (1.3)
(1.3)
其中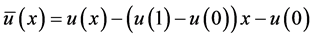 ,所以方程(1.1)等价于方程(1.3),因此为了方便叙述,在下面的章节中我们将讨论方程(1.3),并且仍然用
,所以方程(1.1)等价于方程(1.3),因此为了方便叙述,在下面的章节中我们将讨论方程(1.3),并且仍然用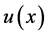 代替
代替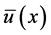 。
。
近些年来,对于(1.3)的形式研究很是广泛,例如
根据ADM方法,问题(1.1)可以被写成如下的算子方程形式
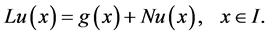 (1.4)
(1.4)
其中 是二阶线性算子,
是二阶线性算子,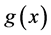 是源点函数,
是源点函数,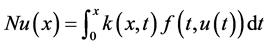 是一个非线性算子。
是一个非线性算子。
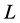 的逆算子定义为
的逆算子定义为
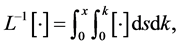 (1.5)
(1.5)
将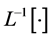 作用在(1.4)的两边,并且用用条件
作用在(1.4)的两边,并且用用条件 ,我们可以得到
,我们可以得到
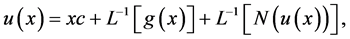 (1.6)
(1.6)
其中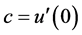 是一个需要求解的未知参数。
是一个需要求解的未知参数。
接下来根据ADM分解方法,将解 和非线性项
和非线性项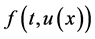 分别分解为
分别分解为
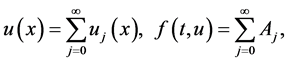 (1.7)
(1.7)
其中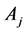 可以通过使用Adomian多项式得到,多项式的表达式为
可以通过使用Adomian多项式得到,多项式的表达式为
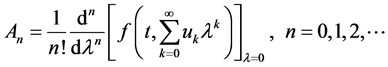 (1.8)
(1.8)
将(1.7)代入(1.6)中,得到
 (1.9)
(1.9)
比较(1.9)等式的两边,有
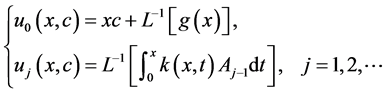 (1.10)
(1.10)
则(1.3)的解可以表示为
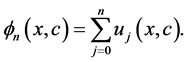 (1.11)
(1.11)
这里级数解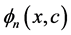 是依赖未知参数
是依赖未知参数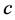 的,所以本文为了避免求解带有未知参数
的,所以本文为了避免求解带有未知参数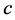 的方程组带来的大量的运算,采用了以下方法的运算形式。
的方程组带来的大量的运算,采用了以下方法的运算形式。
2. 新的方法
在这一节中我们首先考虑如下的线性边值问题
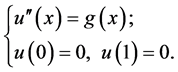 (2.1)
(2.1)
此时(2.1)的解可以通过用再生核方法求解,令
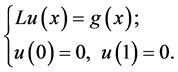 (2.2)
(2.2)
由前面的章节可知(2.1)和(2.2)是等价的,为了应用再生核求解方程(2.2),需要创建一个满足边值条件的再生核空间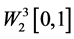 。
。
定义2.1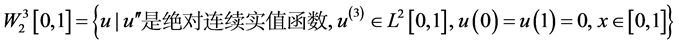 并且内积和范数分别为
并且内积和范数分别为
 (2.3)
(2.3)
定理2.2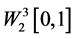 是再生核空间,即存在一个函数
是再生核空间,即存在一个函数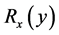 ,对于每一个固定的
,对于每一个固定的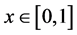 ,
,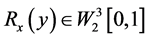 ,并且对于任意的
,并且对于任意的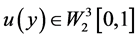 ,且
,且
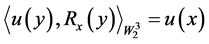 ,再生核
,再生核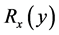 定义为
定义为
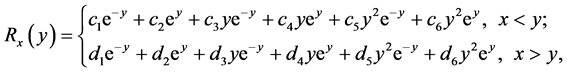 (2.4)
(2.4)
其中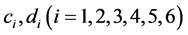 是待定系数。
是待定系数。
定理2.3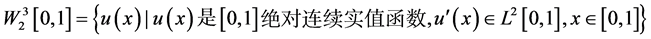 ,同时内积和范数分别定义为
,同时内积和范数分别定义为
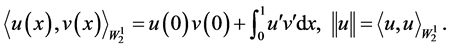 (2.5)
(2.5)
此时存在唯一的再生核函数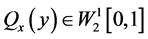 并且
并且
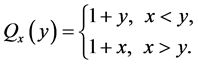 (2.6)
(2.6)
其中定理2.2和定理2.3的证明详见文献 [5] 。
对于方程(1.3),如果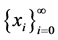 在
在 上是稠密的,令
上是稠密的,令 ,进而有
,进而有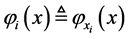 ,其中
,其中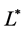 是
是 的共轭算子,即
的共轭算子,即
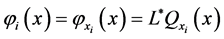 (2.7)
(2.7)
引理2.4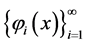 是
是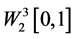 中的完全系,通过施密特标准正交化过程得到
中的完全系,通过施密特标准正交化过程得到 中的正交系
中的正交系 。
。
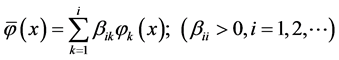 (2.8)
(2.8)
其中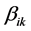 是正交化系数。
是正交化系数。
定理2.5 如果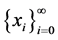 在
在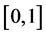 是稠密的,则(2.2)的解可以表示为
是稠密的,则(2.2)的解可以表示为
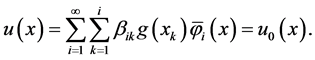 (2.9)
(2.9)
引理2.4和定理2.5的证明详见文献 [6] 。
引理2.6 若令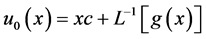 ,即
,即 也就是(1.6)等式的右端的线性部分,则(1.6)的等价形式可以写成
也就是(1.6)等式的右端的线性部分,则(1.6)的等价形式可以写成
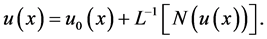 (2.10)
(2.10)
其中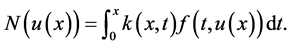
证明 将(2.10)的两边求两阶导数,得到
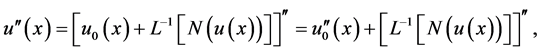 (2.11)
(2.11)
由上一节知道
 (2.12)
(2.12)
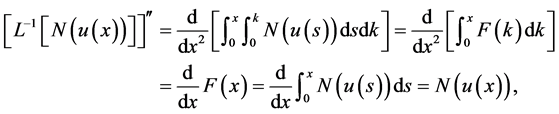 (2.13)
(2.13)
其中 ,将(2.12)和(2.13)代入到(2.11),得到
,将(2.12)和(2.13)代入到(2.11),得到
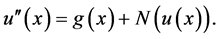
现在方程(1.3)可以写成它的等价形式并使用ADM方法可以得到
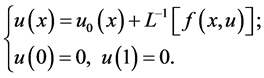 (2.14)
(2.14)
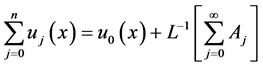 (2.15)
(2.15)
比较(2.15)等式的左右两边,可以得到
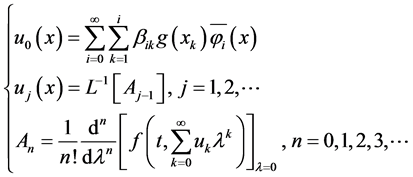 (2.16)
(2.16)
(2.16)给出了方程(1.3)的最终形式,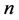 次截断得到的级数解为
次截断得到的级数解为
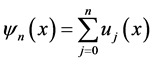 。 (2.17)
。 (2.17)
3. 收敛性分析
定理3.1 若非线性方程中的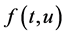 满足Lipschitz条件(1.2),并且有
满足Lipschitz条件(1.2),并且有 ,若
,若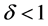 ,
, ,
,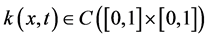 ,并且
,并且 。则级数解
。则级数解 即为(1.3)的解,其中
即为(1.3)的解,其中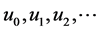 是由(2.16)得到的。
是由(2.16)得到的。
证明 由(2.17)得到
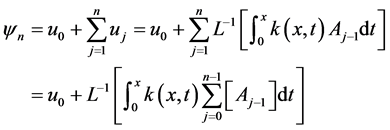 (3.1)
(3.1)
易知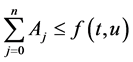 ,得到
,得到
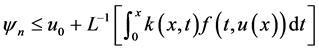 。 (3.2)
。 (3.2)
对于任意的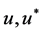 ,考虑
,考虑
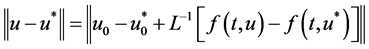 ,(3.3)
,(3.3)
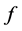 满足Lipschitz 条件,并且
满足Lipschitz 条件,并且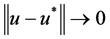 ,得到
,得到
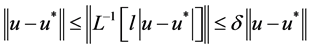 , (3.4)
, (3.4)
由上式,得到
 , (3.5)
, (3.5)
对于任意的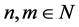 ,
, ,有
,有
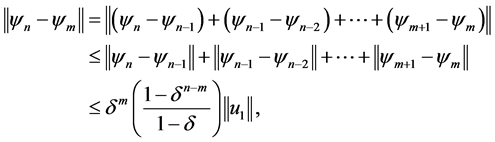 (3.6)
(3.6)
因为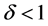 ,所以
,所以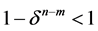 ,并且
,并且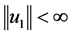 ,则
,则
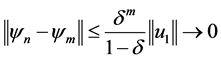 , (3.7)
, (3.7)
此时存在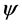 ,使得
,使得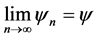 ,因此我们有
,因此我们有 ,即
,即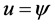 。证毕。
。证毕。
4. 数值算例
下面考虑如下模型:
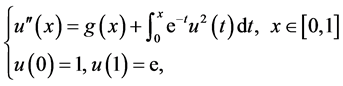 (4.1)
(4.1)
真解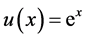 ,
,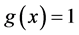 ,现在我们应用本文的方法,先将上述模型齐次化,令
,现在我们应用本文的方法,先将上述模型齐次化,令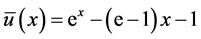 ,则方程组等价于
,则方程组等价于
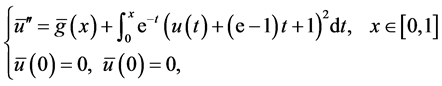 (4.2)
(4.2)
其中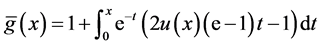 ,此时真解为
,此时真解为 。
。
在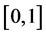 上选择6个节点进行计算。
上选择6个节点进行计算。
为了展示提出新的方法的准确性和有效性,因此定义了如下绝对误差函数
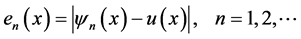 (4.3)
(4.3)
其中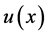 是真解,
是真解,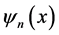 是用新方法得到的
是用新方法得到的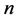 次截断级数解,下面表1中将给出文献 [7] 中应用新方法得到的绝对误差
次截断级数解,下面表1中将给出文献 [7] 中应用新方法得到的绝对误差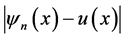 和用改进后的ADM方法给出的绝对误差
和用改进后的ADM方法给出的绝对误差 之间的比较,结果如下表1。
之间的比较,结果如下表1。

Table 1. Comparison of the absolute error of Example 4.1 by using new method and modified ADM decomposition method in the paper [7]
表1. 模型(4.1)中用新方法和改进的ADM分解方法得到的绝对误差比较 [7]
5. 结论
本文主要阐述了应用RKM方法和ADM方法求解一类带有边值问题的积分微分方程,此方法主要优点是避免了求解带有未知参数的方程组,节省了一定的计算量,并且文中给出了收敛性分析和算例,用来佐证方法的有效性。