1. 引言
在经济学、管理学、心理学等众多领域的研究中都需要讨论各个变量之间的关系,尤其是自变量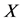 和因变量
和因变量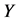 之间是怎样相互影响的,而第三变量是学者探讨自变量和因变量之间关系的重要考虑因素。第三变量在模型中的作用不同会产生不同的效应,如中介效应和调节效应[1] 。
之间是怎样相互影响的,而第三变量是学者探讨自变量和因变量之间关系的重要考虑因素。第三变量在模型中的作用不同会产生不同的效应,如中介效应和调节效应[1] 。
一种模型不仅仅包含3个变量,还可以同时包含中介变量和调节变量。温忠麟等研究的有中介的调节模型即有中介变量又有调节变量 [2] 。有中介的调节模型指的是自变量对因变量的效应受到中介变量和调节变量的影响, 而调节效应则部分或全部通过中介变量起作用,近而影响因变量。国内外学者对有中介的调节模型的研究主要针对单一的中介变量,但是现实问题中,多个中介变量会同时存在,这类模型称为有多重中介的调节模型。对有多重中介的调节模型进行比较系统的分析不仅具有理论价值,而且还能为解决实际问题提供工具。本文试图在已有文献的基础上概括有多重中介的调节模型以及模型的检验方法,并结合实例进行验证。
2. 有多重中介的调节模型
在有中介的调节模型研究中,当多个变量同时起中介作用时,其作用方式既可能是同时性的,也可能是顺序性的,还有可能是两者的复合。
2.1. 有多个并列中介的调节模型
Stillman等在多重中介模型实证分析发现,生活目标感知、正确的价值观、自我效能和自我价值感知同时发挥中介作用 [3] 。当多条中介路径在有中介的调节模型中同时存在,且中介作用同时发生时,这种模型称为有多个并列中介的调节模型。有多个并列中介的调节模型表现形式如图1所示。
温忠麟在有中介的调节模型中给出了有中介的调节效应的回归方程 [2] ,柳士顺和凌文辁在多重中介模型的分析中探讨了多重中介效应的回归方程 [4] ,由此给出了对应于图1的有多个并列中介的调节效应的回归方程如下:
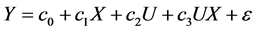
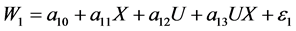
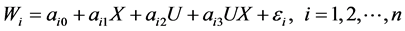

依据路径分析,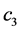 为
为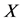 对
对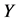 的总调节效应(通过多重中介变量的调节效应),
的总调节效应(通过多重中介变量的调节效应),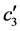 为
为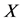 对
对 的直接调节效应,
的直接调节效应,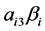 为中介变量
为中介变量 的个别调节效应,因此效应之间有如下关系:
的个别调节效应,因此效应之间有如下关系:
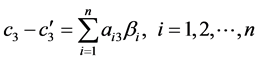
在有多个并列中介的调节模型中,总体间接调节效应为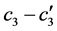 (或者
(或者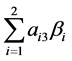 ),因此检验
),因此检验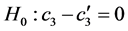 与
与 是等效的,但由于它们的检验统计量不同,会产生不同的检验结果。依据McGuigan和Langholtz研究的统计量,采用t检验方法检验
是等效的,但由于它们的检验统计量不同,会产生不同的检验结果。依据McGuigan和Langholtz研究的统计量,采用t检验方法检验 的显著性。其统计量为:
的显著性。其统计量为:
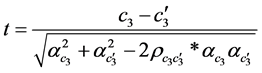
其中,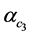 为
为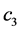 的标准误,
的标准误,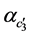 为
为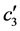 的标准误,
的标准误, 为
为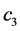 和
和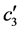 的相关系数 [5] 。
的相关系数 [5] 。
2.2. 有多步中介的调节模型
Liu和Gal研究顾客参与和购买意向之间的关系时发现了以下路径:顾客参与–同理心–与企业亲密性感知–购买意向 [6] ,多个中介变量在自变量和因变量之间按一定的顺序起作用。在有中介的调节模型中,当多条中介路径相互影响,且具有一定的顺序性时,这种模型称为有多步中介的调节模型。因此,有多步中介的调节模型表现形式如图2所示。

Figure 1. Multiple paralleling mediated moderation model
图1. 有多个并列中介的调节模型

Figure 2. Multistep mediated moderation model
图2. 有多步中介的调节模型
与图2相对应的有多步中介的调节效应的回归方程如下:
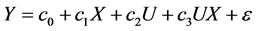
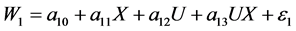
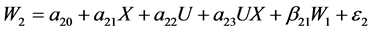
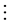
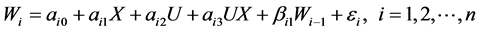
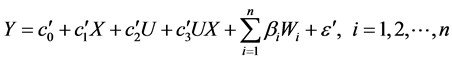
根据MacKinnon在双重中介模型中分析第三路径的中介效应的思路 [7] ,得到在有多步中介的调节模型中,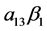 为
为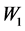 的调节效应,
的调节效应,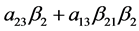 为
为 的调节效应,
的调节效应,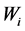 的调节效应为
的调节效应为
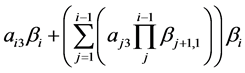 。
。
 对
对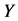 的总体间接调节效应为:
的总体间接调节效应为:
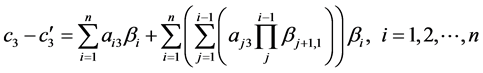
3. 有多重中介的调节模型的检验
3.1. 因果逐步回归检验
从图1和图2可以看出,模型是递归的,由于方程中的所有变量都是显变量,可依次做方程的回归分析替代路径分析。
在回归分析过程中,假设变量已做中心化处理,用适当的软件都可以得到方程中各变量系数的估计值。因果逐步回归检验是依据假设检验的原理去推测模型有没有产生调节效应,其检验过程如下:1) 系数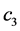 显著(即
显著(即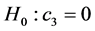 的假设被拒绝),表示
的假设被拒绝),表示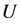 在
在 和
和 之间存在调节效应;2) 系数
之间存在调节效应;2) 系数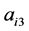 显著,表示
显著,表示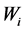 在
在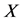 和
和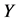 之间存在中介效应,而且在有多步中介的调节模型中,系数
之间存在中介效应,而且在有多步中介的调节模型中,系数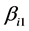 显著,保证
显著,保证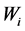 受
受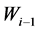 的影响;3) 系数
的影响;3) 系数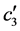 和
和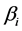 显著,表示调节效应项
显著,表示调节效应项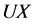 通过中介变量
通过中介变量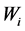 影响因变量
影响因变量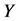 。所以,当系数都显著时,它表明存在通过多重中介变量的调节效应,此时如果系数
。所以,当系数都显著时,它表明存在通过多重中介变量的调节效应,此时如果系数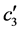 不显著,则调节效应完全通过中介变量起作用。
不显著,则调节效应完全通过中介变量起作用。
3.2. 个别调节效应的Bootstrap检验
在有多重中介的调节模型中,使用Bootstrap方法对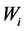 产生的个调节效应
产生的个调节效应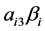 (或
(或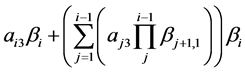 )进行显著性检验。
)进行显著性检验。
在中介效应的检验中使用Sobel检验 [8] ,但是Sobel检验的有效性存在弊端,因为这个检验要求 服从正态分布,但是
服从正态分布,但是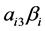 通常并不一定服从正态分布,所以Sobel检验不够准确。另一种常用方法是构建一个对称的置信区间
通常并不一定服从正态分布,所以Sobel检验不够准确。另一种常用方法是构建一个对称的置信区间 进行效应分析检验 [9] ,其中
进行效应分析检验 [9] ,其中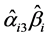 和
和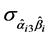 分别为调节效应生成的估计值和标准误,如果0不包含在置信区间内,说明调节效应显著,0包含在置信区间内,说明调节效应不显著。使用对称置信区间法的先决条件是
分别为调节效应生成的估计值和标准误,如果0不包含在置信区间内,说明调节效应显著,0包含在置信区间内,说明调节效应不显著。使用对称置信区间法的先决条件是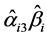 为正态分布,如果不在正态分布下,使用基于标准正态分布的临界z值是不正确的,而实际上
为正态分布,如果不在正态分布下,使用基于标准正态分布的临界z值是不正确的,而实际上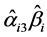 的绝大多数情况下都不是正态分布,因此,对称置信区间法也是不准确的。Preacher和Hayes提出了检验效应分析的Bootstrap方法 [10] ,Bootstrap方法在效应分析中对
的绝大多数情况下都不是正态分布,因此,对称置信区间法也是不准确的。Preacher和Hayes提出了检验效应分析的Bootstrap方法 [10] ,Bootstrap方法在效应分析中对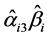 的分布没有任何限制,还可以得到不对称的置信区间,且适用于中、小样本。
的分布没有任何限制,还可以得到不对称的置信区间,且适用于中、小样本。
Bootstrap方法模拟了从总体中随机抽取大量新的子样本的过程,它的原理是以原始样本为“总体”,通过有放回的重复抽样,获得大量新的子样本并得到其统计量。Bootstrap方法分为三个步骤。第一,以样本容量为n的原始样本为基础,在保证每个样本被抽到的概率均为1/n的情况下进行有放回的重复抽样,获得一个新的Bootstrap样本(样本容量为n);第二,从获得的新Bootstrap样本中计算出相应的个别调节效应的估计值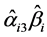 ;第三,重复步骤1和2共m次(
;第三,重复步骤1和2共m次(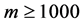 ),因此得到调节效应的点估计值,即m个调节效应估计值的均值。将m个调节效应的估计值
),因此得到调节效应的点估计值,即m个调节效应估计值的均值。将m个调节效应的估计值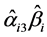 按数值大小排列,得到序列C,将序列C的第2.5百分位数记作置信区间下限,将第97.5百分位数记作置信区间上限,由此估计95%的调节效应置信区间。如果置信区间不包括0,说明调节效应显著,置信区间包括0,说明调节效应不显著。
按数值大小排列,得到序列C,将序列C的第2.5百分位数记作置信区间下限,将第97.5百分位数记作置信区间上限,由此估计95%的调节效应置信区间。如果置信区间不包括0,说明调节效应显著,置信区间包括0,说明调节效应不显著。
4. 有多重中介的调节模型的实证分析
要研究的是压力 对负性情绪
对负性情绪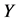 的影响,数据来自对武汉理工大学200名大一学生的问卷调查。该项研究中,压力可以直接影响负性情绪,还可以通过中介变量(认知倾向
的影响,数据来自对武汉理工大学200名大一学生的问卷调查。该项研究中,压力可以直接影响负性情绪,还可以通过中介变量(认知倾向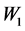 、应对策略
、应对策略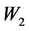 )和调节变量(人际关系
)和调节变量(人际关系 )影响负性情绪。由于认知倾向
)影响负性情绪。由于认知倾向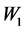 和应对策略
和应对策略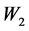 的相关系数r = 0.353,相关性很弱,因此假设模型为有多个并列中介的调节模型。运用SPSS 18.0和Amos 17.0软件对数据进行统计分析,给出相对应的回归方程及回归系数的t值和p值。结果见表1。
的相关系数r = 0.353,相关性很弱,因此假设模型为有多个并列中介的调节模型。运用SPSS 18.0和Amos 17.0软件对数据进行统计分析,给出相对应的回归方程及回归系数的t值和p值。结果见表1。
根据因果逐步回归检验的方法,方程1中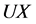 的回归系数
的回归系数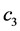 (t = 3.492, p < 0.05)显著,所以人际关系
(t = 3.492, p < 0.05)显著,所以人际关系 在压力
在压力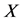 和负性情绪
和负性情绪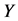 之间起到调节作用。方程2和方程3中
之间起到调节作用。方程2和方程3中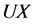 的回归系数
的回归系数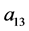 (t = 2.217, p < 0.05)和
(t = 2.217, p < 0.05)和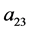 (t = 2.175, p < 0.05)显著,说明认知倾向
(t = 2.175, p < 0.05)显著,说明认知倾向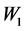 和应对策略
和应对策略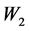 在压力
在压力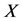 和负性情绪
和负性情绪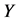 间起到中介作用。方程4中
间起到中介作用。方程4中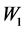 的回归系数
的回归系数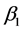 (t = 2.157, p < 0.05)和
(t = 2.157, p < 0.05)和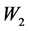 的回归系数
的回归系数 (t = 5.013, p < 0.001)显著,说明乘积项UX通过
(t = 5.013, p < 0.001)显著,说明乘积项UX通过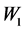 和
和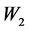 对负性情绪起作用。
对负性情绪起作用。
在压力和负性情绪的关系中,人际关系通过多重中介的调节效应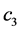 为0.302,其中直接调节效应
为0.302,其中直接调节效应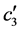 为0.176,间接调节效应
为0.176,间接调节效应 为0.126。因为人际关系和压力的交互项
为0.126。因为人际关系和压力的交互项 对负性情绪的调节效应显著(
对负性情绪的调节效应显著(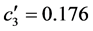 , t = 2.341, p = 0.022 < 0.05),所以认知倾向
, t = 2.341, p = 0.022 < 0.05),所以认知倾向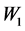 和应对策略
和应对策略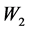 起部分中介的作用。
起部分中介的作用。
使用Bootstrap方法计算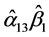 和
和 的置信区间。由表2可知,
的置信区间。由表2可知,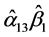 的95%置信区间为[0.002, 0.06],
的95%置信区间为[0.002, 0.06],

Table 1. Regression result analysis
表1. 回归结果分析

Table 2. Bootstrap analysis of significance testing for regulatory effect
表2. 对调节效应显著性检验的Bootstrap分析
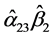 的95%置信区间为[0.01, 0.09],各条路径的95%置信区间都没有包括0,验证了人际关系
的95%置信区间为[0.01, 0.09],各条路径的95%置信区间都没有包括0,验证了人际关系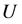 在压力
在压力 与负性情绪间
与负性情绪间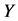 的调节效应(通过应对策略和认知倾向的调节效应)。所以,压力和负性情绪的关系可以建立有多重中介的调节模型。
的调节效应(通过应对策略和认知倾向的调节效应)。所以,压力和负性情绪的关系可以建立有多重中介的调节模型。
5. 结论
本文提出的有多重中介的调节模型针对的是中介变量和调节变量同时存在自变量和因变量之间,且中介变量不止一个的情况。基础模型为有多个并列中介的调节模型和有多步中介的调节模型,其他复杂模型是这两种模型的组合。
本文的模型中涉及的变量都是显变量,但所讨论的模型路径图和分析思路对于潜变量同样适用。有多重中介的调节模型分析流程通过回归方程展现出来,进行有多重中介的调节效应分析时使用不需要以正态性、大样本作为前提假设的Bootstrap方法进行检验,并通过实例进行演示。
基金项目
国家自然科学基金项目(81271513);国家自然科学基金重点基金项目(91324201);教育部人文社科青年基金项目(14YJCZH143);中央高校基本研究业务费专项资金资助(WUT: 2014-la-035)。