1. 引言
量子力学中微观客体的自旋是最不好理解的物理量。把电子自旋看成经典球体机械自转是不正确的。那样,“运动电子的边缘线速要超过光速”。电子自旋角动量S及自旋磁矩ms只能看着是电子自身的内禀属性,自旋是没有真实物理过程依托的假设。自旋是电子的“转动”,有角动量特征,又不能理解为电子的自转,很是无奈。自旋到底是什么,一直困扰着人们,难道它只能是无法认识物理过程的点粒子的属性吗?我们的回答是:不是。
双4维时空量子力学描述中,电子是转动的场物质球,因为在运动参考系中,微观客体的质量可变,因此,球半径随球的运动状态改变而改变。运动微观客体的转动频率加快,半径减小,保证了球的边缘线速不超过光速,维护了与相对论的一致性。自旋有明确的物理模型支撑,有明确的物理概念、角动量量度及物理过程对应。电子自旋S及自旋磁矩ms都可以通过模型来计算 [1] [2] 。
假定场物质球在复数空间转动,或者假定电子自身参考系就在复空间,在闵氏4维时空观察转动场物质球的运动,则形成场物质的波动运动,它就是德布罗意物质波。物质波是物理波 [1] [2] 。
2. 量子力学电子自旋、自旋波函数假设
2.1. 非相对论量子力学电子自旋、自旋波函数假设及自旋算符
量子力学中电子自旋及自旋磁矩是电子自身的内禀属性( [3] , p. 196)。称为内禀角动量和内禀磁矩。它们的存在表明电子还有一个新的自由度。表现在自旋波函数中。
电子自旋波函数又称旋量波函数,记为: ,Sz代表自旋角动量S在z轴方向上的投影(实为自身参考系),自旋向上
,Sz代表自旋角动量S在z轴方向上的投影(实为自身参考系),自旋向上 ,自旋向下
,自旋向下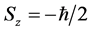 。在有些情况下,自旋波函数可以分离变量,即:
。在有些情况下,自旋波函数可以分离变量,即:
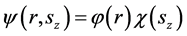
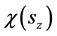 是描述自由微观客体自旋态的波函数,一般形式为
是描述自由微观客体自旋态的波函数,一般形式为
 (4.4.1)
(4.4.1)
a,b是自旋态波函数的两个分量。特例:本征值: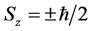 的本征态
的本征态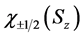 记为
记为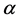 、
、
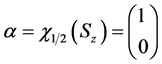
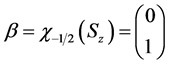
 与
与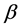 构成电子自旋态空间的一组正交完备基,一般自旋态
构成电子自旋态空间的一组正交完备基,一般自旋态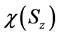 可用它们来展开,即叠加态
可用它们来展开,即叠加态
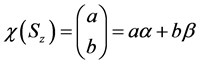 (4.4.2)
(4.4.2)
或
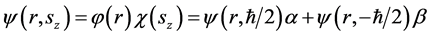
叠加态:
 (4.4.3)
(4.4.3)
的演化是可逆的,相干的,决定论的,遵循量子测量的U过程和薛定谔方程。不过,这里自旋态波函数是作为微观客体整体波函数的一部分纳入其中的,是非相对论的( [3] , pp. 196-208)。
考虑自旋有角动量特征,假设自旋S的三个分量Sx,y,z有与轨道角动量三个分量lx,y,z相同的对易关系,同时引进泡利算符 (无量纲),有
(无量纲),有

由于S沿任何方向的投影只能取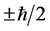 ,所以
,所以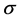 沿任何方向的投影只能取±1。自旋算符作用于自旋本征态,有
沿任何方向的投影只能取±1。自旋算符作用于自旋本征态,有

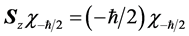
量子力学中,自由微观客体自旋波函数完全是一种假设和人为的数学构造。自旋角动量S没有真实物理过程对应,只能是假设。自旋到底是什么,一直困扰着人们。它纯粹是点粒子的属性吗?我们认为不是。但是,非相对论量子力学电子是质点,电子自旋、自旋波函数及自旋算符,讨论中也不涉及自身参考系,对自旋的认知很难深入。
双4维时空量子力学描述中,电子是场物质球,自旋有明确的物理模型支撑,有明确的物理概念、角动量量度及物理过程对应,在自身参考系,自旋很好理解。
2.2. 相对论量子力学电子自旋及自旋波函数假设
1) 电子自旋算符Sj及自旋波函数Bα在自身参考系
为了求出狄拉克(Dirac)微观客体(电子)的自旋值,必须知道其相应的自旋算符。计及自旋角动量S,狄拉克粒子轨道角动量l将不是守恒量,有不对易关系 ;但总角动量
;但总角动量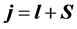 是守恒量,有对易关系
是守恒量,有对易关系 等,可以得到方程( [4] , p. 19):
等,可以得到方程( [4] , p. 19):

由此,可以求得自旋算符S及其分量Sj,j = x、y、z。

狄拉克粒子S三个分量Sx,Sy,Sz的本征值为 。而
。而
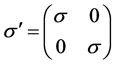
因为自旋算符S是4 × 4矩阵,故自旋波函数应该是4个,记为Bα (α = 1, 2, 3, 4)所以有
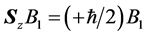 ,
,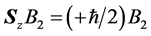
 ,
,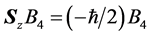
自旋波函数必须是正交归一的
故
 ,
,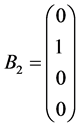 ,
,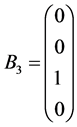 ,
,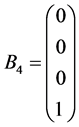 (4.4.4)
(4.4.4)
自旋算符Sj只与泡利矩阵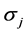 有关,与时空坐标和动量无关,自旋算符Sj及其自旋波函数Bα是在微观客体自身参考系确定的( [4] , p. 19)。
有关,与时空坐标和动量无关,自旋算符Sj及其自旋波函数Bα是在微观客体自身参考系确定的( [4] , p. 19)。
2) 自旋波函数Bα在自身参考系的进一步讨论
我们来从微观客体自身参考系求出狄拉克方程的解,由此进一步确证自旋波函数Bα在自身参考系。
狄拉克方程一般写成如下4维形式
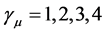 ,
,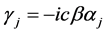 ,
,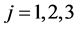 ,
,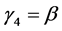
而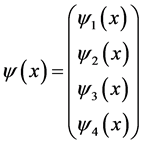
狄拉克方程里4个γμ矩阵构成16个独立4 × 4矩阵,因此,波函数ψ(x)是一个4 × 1矩阵。
自旋算符Sj只与泡利矩阵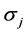 有关,与时空坐标和动量无关,因此,自旋是在粒子自身参考系确定的,Hamilton算符
有关,与时空坐标和动量无关,因此,自旋是在粒子自身参考系确定的,Hamilton算符 ,狄拉克方程应为
,狄拉克方程应为
 (4.4.5)
(4.4.5)
而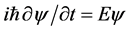
故
粒子自身参考系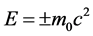 ,
,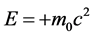 取正号+,
取正号+, 取负号−
取负号−
故
 (4.4.6)
(4.4.6)
ψ(x)是β的本征函数,±1则为本征值,β是4 × 4矩阵,因此,旋量波函数ψ(x)的本征函数一共有4个:
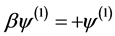 ,
,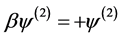 (4.4.7)
(4.4.7)
 ,
,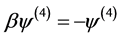 (4.4.8)
(4.4.8)
将(4.4.7)、(4.4.8)代入方程(4.4.5),考虑旋量波函数ψ(x)与空间坐标无关,有 得方程
得方程
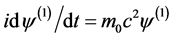 ,
,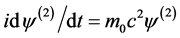
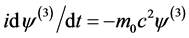 ,
,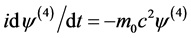
解上方程,得解
 ,
, ,
, ,
,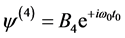 (4.4.9)
(4.4.9)
式中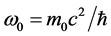 ,(4.4.9)代入(4.4.7)、(4.4.8)得B1、B2、B3、B4满足的本征值方程
,(4.4.9)代入(4.4.7)、(4.4.8)得B1、B2、B3、B4满足的本征值方程
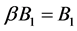 ,
,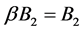 ,
,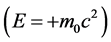
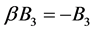 ,
,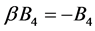 ,
,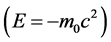
而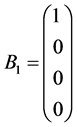 ,
, ,
, ,
,
这正是方程(4)。故
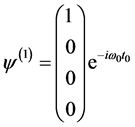 ,
,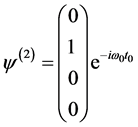 ,
, ,
, (4.4.10)
(4.4.10)
这就是微观客体自身参考系的旋量波函数,具体地讲,微观客体的自旋状态是由旋量波函数振幅Bα来描写的。
微观客体自身参考系的旋量波函数自动分成两部分:描写微观客体时空运动特性的相因子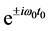 和与时空运动无关的旋量振幅Bα;后者与微观客体内部自由度相关,所以把Bα理解为自旋波函数。
和与时空运动无关的旋量振幅Bα;后者与微观客体内部自由度相关,所以把Bα理解为自旋波函数。
在微观客体自身参考系,旋量波函数按能量正负分成:正能解ψ(1)、ψ(2)和负能解ψ(3)、ψ(4)。但是无论正能解和负能解又都分为两种自旋态:ψ(1)、ψ(3)描写自旋角动量在空间第3轴(Z轴)的投影为+ħ/2的态,ψ(2)、ψ(4)描写自旋角动量在空间第3(Z轴)的投影为−ħ/2的态。旋量振幅Bα张成一个4维双旋量空间(两个2维空间的直和),它预示旋量波函数4个分量与狄拉克方程4类不同能量符号、不同自旋取向的解之间存在着深刻内在联系。这应该有一个可理解的量子力学图像,可惜现在看不到任何物理图像。但是在双4维时空量子力学描述中,结合正负电子、正负能量对应正、负康普顿动量等概念,旋量波函数4个分量的物理意义,与微观客体旋转场物质球模型的对应,似乎已经呼之欲出。
3. 双4维时空量子力学波函数ψ0、ψ与狄拉克波函数Bα、ψ
3.1. 双4维时空自旋波函数ψ0与狄拉克自旋波函数Bα之比较
双4维时空量子力学描述中,微观客体是转动场物质球,自旋由场物质球在复空间的转动定义。其自旋波函数 [1] [2]
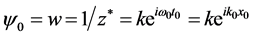
对于狄拉克正、负电子,它刚好对应转动方向相反的两个场物质球。由于双4维时空量子力学描述中,相对论能量表达式可表述成:
 或
或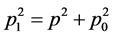
在微观客体自身参考系,p = 0,故有
 (4.4.11)
(4.4.11)
它表明在自身参考标系内,正、负电子又各自有两个转动方向相反的对应。如果一个转动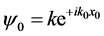 表示电子自旋朝上,另一个
表示电子自旋朝上,另一个 则表示电子自旋朝下;正电子也一样。若自身参考标系就在复空间,正、负电子刚好构成复空间两个转动的2维空间的直和,张成一个4维双旋量空间。这就是狄拉克相对论量子力学的物理图象。这里,我们把正、负能量通过场物质球模型转换成了正、负动量 [1] [2] 。动量是可以有正负的,用动量的正负消除了负能量危机。
则表示电子自旋朝下;正电子也一样。若自身参考标系就在复空间,正、负电子刚好构成复空间两个转动的2维空间的直和,张成一个4维双旋量空间。这就是狄拉克相对论量子力学的物理图象。这里,我们把正、负能量通过场物质球模型转换成了正、负动量 [1] [2] 。动量是可以有正负的,用动量的正负消除了负能量危机。
双4维时空量子力学描述中,物质波波函数与概率波(概率幅)尽管物理内含有别,但数学形式相同 [1] [2] ,数学运作无障碍,因此场物质球在复空间自身参考系两个相反方向的转动波函数
 ,
,
正是自身参考系狄拉克方程

中的旋量波函数
 (4.4.12)
(4.4.12)
只是k = A = Bα。量子力学原有数学方法完全可用。一个将实空间定义的质点对应的矢量放在实空间转动,闵氏空间有一个复数描述的概率波;而另一个则将实在的场物质球,用其对应的曲率矢量放在复空间转动,双4维复时空有一个复数描述的物质波,|ψ|2描述场物质密度分布。但后者微观客体自身物理图像清晰,自旋很好理解。自旋波函数对应的4个分量,是因为正、负电子自旋各有两个分量的缘故。k = A = Bα得到解释。
显然,微观客体的自旋,在自身参考系,是相对于自在实体R0 = ħ/m0c而言的,描述的是本体的性质,具有不变性。
3.2. 狄拉克平面波波函数与双4维时空平面波波函数
1) 狄拉克方程的平面波波函数
一个以动量p作自由运动的狄拉克粒子,假定用如下平面波来描述( [3] , p. 24):
 (4.4.13)
(4.4.13)
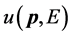 是旋量波函数的振幅,式中
是旋量波函数的振幅,式中
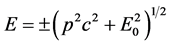
在微观客体自身参考系:p = 0,
这就是旋量波函数(10)。
为了求得任意参考系里振幅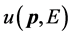 的具体形式,将波函数(4.4.13)代入狄拉克方程,我们可以得到
的具体形式,将波函数(4.4.13)代入狄拉克方程,我们可以得到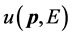 满足的方程
满足的方程
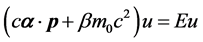 (4.4.14)
(4.4.14)
求解方程(4.4.14),并选取P的方向为Z方向得
对于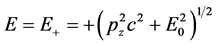 选取
选取
第一组解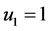 ,
,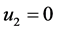 ,
,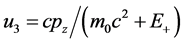 ,
,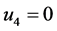
第二组解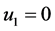 ,
, ,
, ,
,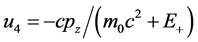
对于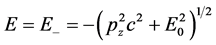 选取
选取
第一组解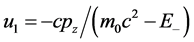 ,
, ,
,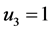 ,
,
第二组解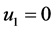 ,
, ,
, ,
,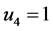
解方程(4.4.14)有4个线性独立解
 ,
, (4.4.15-1)
(4.4.15-1)
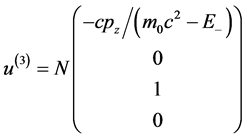 ,
,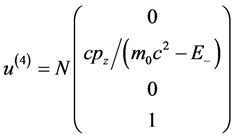 (4.4.15-2)
(4.4.15-2)
其中N为归一化因子。
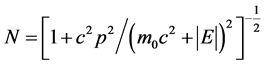
(4.4.15-1) (4.4.15-2)式中u(1)、u(2)属于能量E = E+的本征态,对应电子,u(3)、u(4)属于能量E = E−的本征态,对应正电子。当p = 0时,旋量波函数的振幅u回到自旋波函数Bα,即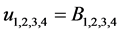 。u(1)和u(3)态中,微观客体的自旋角动量的Z分量为ħ/2,u(2)和u(4)态微观客体的自旋角动量的Z分量为−ħ/2。必须注意:自旋是在微观客体自身参考系定义的,与微观客体在动系的时空坐标无关。
。u(1)和u(3)态中,微观客体的自旋角动量的Z分量为ħ/2,u(2)和u(4)态微观客体的自旋角动量的Z分量为−ħ/2。必须注意:自旋是在微观客体自身参考系定义的,与微观客体在动系的时空坐标无关。
2) 双4维时空平面波波函数
双4维时空量子力学描述中,微观客体是转动的场物质球。在曲率复空间表示为
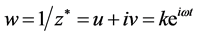
ω为微观客体场物质球旋转的角频率 [1] [2] 。
设微观客体自身的坐标系为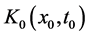 ,“静态微观客体内部场物质的旋转运动”,以时间t0为自由变量的场物质球旋转运动方程是
,“静态微观客体内部场物质的旋转运动”,以时间t0为自由变量的场物质球旋转运动方程是
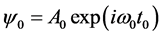 (4.4.16)
(4.4.16)
式中, 。ψ0就是量子力学中微观客体自身参考系定义的旋量波函数,A0 = Bα刚好是自旋波函数。
。ψ0就是量子力学中微观客体自身参考系定义的旋量波函数,A0 = Bα刚好是自旋波函数。
在观测系,利用洛仑兹变换 [1] [2] :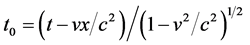 代入式(4.4.16)得
代入式(4.4.16)得
 (4.4.17)
(4.4.17)
式中 ,
,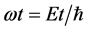 ,
,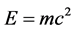 ,
,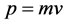 ,
,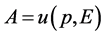 。对自由微观客体A是常数(归一化因子)。
。对自由微观客体A是常数(归一化因子)。
(4.4.17)式描述的是场物质的波动运动——旋量波函数。它就是德布罗意物质波,是物理波。物质波的本质是旋转场物质的波动运动!
对物质波(4.4.17)有两种认知与处理方法:
1) (4.4.17)式是物质波在闵氏空间的复数描述,振幅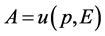 ,类似交流电的复数描述。这种处理方法意义有限。而且
,类似交流电的复数描述。这种处理方法意义有限。而且 也不能直接理解为概率密度分布,而是描述与场物质球相联系的场物质密度分布。只是在量子测量中,场物质密度分布可以映射成概率密度分布。量子力学原有数学方法不变。
也不能直接理解为概率密度分布,而是描述与场物质球相联系的场物质密度分布。只是在量子测量中,场物质密度分布可以映射成概率密度分布。量子力学原有数学方法不变。
2) 为了进一步搞清楚物质波的物理本质,结合场物质球模型及曲率坐标k,我们发现物质波传播在双4维复时空W(x,k)中。双4维复时空是闵氏时空的复数拓展,并展现在波函数的相位上 [1] [2] ,类似费曼路径积分的相位积分操作。双4维复时空中旋量波函数形式表述为
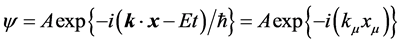 (4.4.18)
(4.4.18)
 ,
,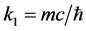 ,
,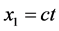 ,
,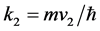 ,
,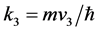 ,
, ,
, 。m为运动质量。能量E = E+的对应表述为k = +k,E = E-的对应表述为k = −k,刚好表达复空间两个相反的转动,这就是电子和正电子 [1] [2] 。双4维复时空的长处在于它把(4.4.17)式中的能量和动量统归于变量k,而时间则归于变量x1(=ct)。对时间的微商则变为:
。m为运动质量。能量E = E+的对应表述为k = +k,E = E-的对应表述为k = −k,刚好表达复空间两个相反的转动,这就是电子和正电子 [1] [2] 。双4维复时空的长处在于它把(4.4.17)式中的能量和动量统归于变量k,而时间则归于变量x1(=ct)。对时间的微商则变为: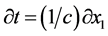 。对于波函数的定态则有
。对于波函数的定态则有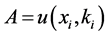 ,i = 2,3,4,回到双4维时空量子力学描述定态波函数的讨论。
,i = 2,3,4,回到双4维时空量子力学描述定态波函数的讨论。
当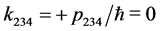 时,
时,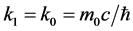 ,
,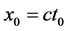 (4.4.18)式表述为
(4.4.18)式表述为
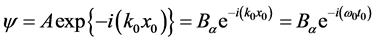 (4.4.19)
(4.4.19)
上式同样回到旋量波函数(4.4.10)。这里有A = Bα。ψ是方程
的解。
4. 双4维时空量子力学描述中电子自旋的计算 [1] [2]
4.1. 场物质球模型中电子的半径
“静态”: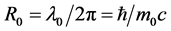 (4.4.20)
(4.4.20)
“运动”: (4.4.21)
(4.4.21)
转动频率:
“静态”: (4.4.22)
(4.4.22)
“运动”: (4.4.23)
(4.4.23)
4.2. 电子自旋的计算
把电子自旋理解为电子机械球体的自转,运动电子的边缘线速度确实要超过光速。但是,双4维时空量子力学描述中,电子不是经典机械球体,电子是场物质球,其形态可变。电子运动速度加快,(4.4.21)式中质量m加大,(4.4.23)式ν1频率加快,(4.4.21)式中电子半径减小,边缘线速总是保持光速,不违背相对论。真实电子是(4.4.20)和(4.4.21)式。在双4维时空中,电子的自旋就是电子场物质球的自转。自转角动量可计算如下:
双4维时空量子力学描述中,R0为场物质球的半径,微观客体位置测不准量是球的直径: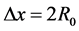 ,动量的测不准量为微观客体的动量:
,动量的测不准量为微观客体的动量: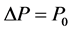 ,按测不准关系式有 [1] [2]
,按测不准关系式有 [1] [2]

所以
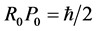
令R0P0 = S,S正是场物质球的自转角动量,电子的自转角动量——自旋S = ħ/2可以由场物质球模型直接计算。考虑到电子自转在何任方向均有上、下两个相反取向,自旋应为Sz = ±ħ/2。

可见,自旋对于点粒子模型是一个内禀属性,没有直接的物理过程对应;但是,自旋对于场物质球模型,完全有可理解的物理过程对应。R0、ħ、P0 = m0c都是常数,具有不变性,所以我们说自旋与微观客体所在的运动参考系时空无关,是在自身参考系定义的。应该说明,自旋与本体直接相关,而本体不可直接观察,因此,自旋也不可直接观察,但有现象表现,所以,量子力学中自旋被理解为点粒子的一个内禀属性。
4.3. 复数时空中场物质球模型对自旋的理解
我们知道,3维空间的一个旋转,对应于复数空间两个幺模旋转[U+(−U)]。即:SU(2)与SO(3)两群间存在2:1的同态关系。而同构是一一对应的同态关系。U(1)与SO(2)是同构关系,意味着:自旋为1粒子的一个旋转(U),对应于SO(2)中同样的一个转动(O)。光子的自旋为1,U(1)旋转可以用来描述光子的自旋。
在物理上,SU(2)中的一个元素,对应于自旋1/2的粒子的波函数在二维表示下的一个转动。它与3维旋转群SO(3)之间2:1的同态关系意味着:如果自旋1/2粒子的一个旋转(U),对应于SO(3)中的某个转动(O)的话,旋转变换(−U),也将对应于同样的一个转动(O) [5] 。狄拉克能量的正、负对应的是正、负电子的统一体系,所以,旋转(U)、(−U),我们认为刚好对应的是电子、正电子两个旋转的合一。
用场物质球在复空间的旋转理解电子的自旋比用场物质球抽象成质点在实空间的旋转理解电子的自旋容易得多。由于SU(2)与SO(3)存在2:1的同态关系,SU(2)中旋转一圈360˚刚好对应SO(3)中旋转二圈720˚。电子的自旋1/2,正是SU(2)中一个旋转(U)的结果,比如顺时针(旋转180˚反向,360˚复位,所以自旋有±1/2之别);正电子的自旋也是1/2,是SU(2)中另一个旋转(−U)的结果,比如逆时针(也是旋转180˚反向,360˚复位,同样自旋有±1/2之别)。而我们的“旋转场物质球电子”正是复数时空中的转动,正、负电子合在一起,直和,可以用SU(2)来描述自旋。自旋是“场物质球”复数时空中的转动对应物,不是实时空点模型的对应物。过去由于复空间的复数与实空间复数对量子力学物理模型上没有作区分,点模型一贯到底,SU(2)、SO(3)的空间性质在相互转换中对模型的依赖也模糊不清,增加了对自旋理解的难度。
自旋为半整数是费米子的特性。说自旋空间中的旋转只等于真实3维空间中旋转角的一半,那是没有考虑它的反粒子所得出的模糊结论。量子力学认为自旋是微观粒子(质点)的内禀特性,经典世界中并无对应物,看来也并不真实。
5. 自旋磁矩ms (内禀磁矩)
5.1. 量子力学中电子的自旋磁矩ms
一个非相对论性的自由微观客体的Hamilton量通常取为
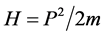 (4.4.24)
(4.4.24)
如果考虑电子还有自旋,自由电子的Hamilton量取为
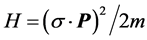 (4.4.25)
(4.4.25)
 为包利矩阵。
为包利矩阵。
在无外场的情况下,(4.4.25)回到(4.4.24)
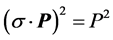 (4.4.26)
(4.4.26)
自旋的作用无体现。它表明,在无外磁场时,自旋对自由微观客体的外在运动状态无影响,或者可以忽略不计。
但在外磁场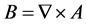 中,H应表述成
中,H应表述成
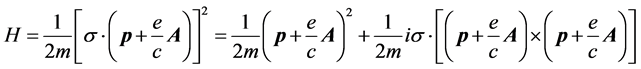 (4.4.27)
(4.4.27)
考虑自旋,与无外场相比,(4.4.27)式右边多出了第二项,简化为
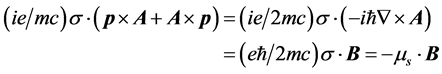 (4.4.28)
(4.4.28)
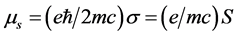 (4.4.29)
(4.4.29)
(4.4.28)式中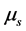 可理解为与自旋s相应的磁矩,称为内禀磁矩。表示内禀磁矩与外磁场B的相互作用。内禀磁矩的值为一个玻尔磁子,
可理解为与自旋s相应的磁矩,称为内禀磁矩。表示内禀磁矩与外磁场B的相互作用。内禀磁矩的值为一个玻尔磁子,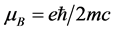 。
。
量子力学得出电子内禀磁矩的值为一个玻尔磁子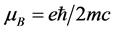 ,完全是借助包利矩阵
,完全是借助包利矩阵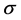 的数学形式在数学运算中得到的。物理模型是点粒子,自旋是微观客体的一种转动属性与外磁场B作用的结果。没有微观客体与电磁场作用的任何物理图像和物理机制对应,纯粹是人为猜测和抽象数学操作与认可。难怪人们说量子力学难懂。
的数学形式在数学运算中得到的。物理模型是点粒子,自旋是微观客体的一种转动属性与外磁场B作用的结果。没有微观客体与电磁场作用的任何物理图像和物理机制对应,纯粹是人为猜测和抽象数学操作与认可。难怪人们说量子力学难懂。
5.2. 双4维时空量子力学描述中自旋磁矩ms的计算
1) 电子自旋磁矩的计算:
a) “静态”电子自旋磁矩的计算
静态电子的自旋磁矩(以下均采用实用单位制)
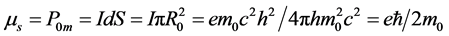 (4.4.30)
(4.4.30)
电子的自旋磁矩等于1个玻尔磁子eħ/2m0。
b) 运动电子自旋磁矩的计算
运动电子的自旋磁矩
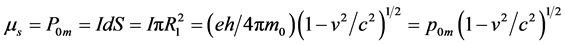 (4.4.31)
(4.4.31)
运动电子的自旋磁矩随电子运动速度的增加而减小。
c) 核磁子P核磁子及质子磁矩Pp的计算
核磁子P核磁子可以精确计算。
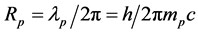 ,
,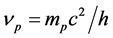 ,
,
核磁子P核磁子的定义
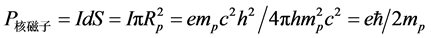 (4.4.32)
(4.4.32)
d) 质子磁矩的计算
质量 。mu、md是上、下夸克的质量。
。mu、md是上、下夸克的质量。
上夸克的自旋磁矩
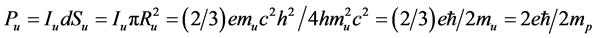 (4.4.33)
(4.4.33)
下夸克的自旋磁矩
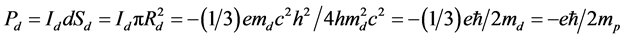 (4.4.34)
(4.4.34)
质子磁矩粗略计算:
上述计算结果与实验相差较大。
质子磁矩精确计算:
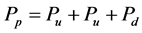
 (4.4.35)
(4.4.35)
当两个上夸克磁倾角α = 37.70时,
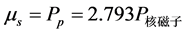 (4.4.36)
(4.4.36)
上述结果与实验符合得很好。
夸克是不可直接观察的,磁倾角假设与实际不会有矛盾。它是综合考虑微观领域所有相互作用的共同结果。即使考虑上夸克与下夸克的质量不相等,我们也可以通过调整磁倾角假设来达到与实验的一致。磁倾角假设是普遍适用的。磁倾角与自旋磁矩实验测量值的对应,就类似本征态与本征值的对应一样。
e) 中子的磁矩精确计算:
一个上夸克磁矩与两个下夸克平行反向,中子的磁矩
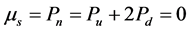
中子的磁矩不等于0,上述假设不正确,磁倾角不是180˚。调整磁倾角达到与实验的一致。

中子的磁矩应该是个负值。如果考虑上、下夸克质量不相等,但通过调整磁倾角α,理论值与实验值也完全可达到精确符合。我们期待实验物理学家的工作。
双4维时空量子力学描述,提供了一个合理的物理模型,对量子力学中原来没有的物理图象和机制给予了展示,补充对量子力学基础的认知,让人们从抽象的纯粹数理运算中走出来,借助物理图像和物理机制理解量子力学。但它并不排斥数学方法,原有的数学方法仍然可用。
6. 结论与讨论
1) 双4维时空量子力学描述中,自旋就是场物质球的自身转动。有明确的物理概念及物理过程对应。
2) 电子、质子、中子等的自旋S及自旋磁矩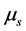 都可以通过场物质球模型来计算。
都可以通过场物质球模型来计算。
3) 能量E = E+的对应表述为k = +p/ħ,E = E−的对应表述为k = −p/ħ,刚好表达复空间两个相反的转动,这就是电子和正电子。它刚好构成2维复空间两个转动的直和,张成一个4维双旋量空间。这就是狄拉克相对论量子力学的物理图象。我们把正负能量通过场物质球模型转换成了正、负动量。动量是可以有正负的,用动量的正负消除了负能量危机。
4) 自旋S = R0P0 = ħ/2,R0、ħ、P0 = m0c都是常数,具有不变性,所以我们说自旋与微观客体的时空坐标无关。
致谢
长期以来,诸多国内外学者对课题研究及论文写作给予了关注与指导,参与了许多讨论,有些还有合作论文发表,在此一并表示衷心感谢。