1. 引言
从化学实验的角度研究一种新的物质,需要有良好的实验环境支撑,有充足的资金来购买仪器设备和试剂,同时还将花费大量人力物力。而用图模型研究分子结构性质的方法,就能避免这些问题,在无硬件设备的条件下获得关于化学物的化学、药学特征。在具体计算模型中,将化学分子的结构用图模型来表示,化学分子的特性就可以用一些参数来衡量,比如PI指数、维纳指数、舒尔茨指数等等。文献 [1] 讲述了拓扑指数在生物学和化学的使用开始于1947年,当时化学家哈罗德.维纳证明有机物化合分子的理化性质之间的化学图表,维纳指数所有无序对简单图G的顶点之间的距离之和,得出维纳指数。文献 [2] 根据1988年对于拓扑指数Hosoya引入Hosoya多项式,定义了维纳指数和相关多项式。Schultz在文献 [3] 中定义了基于结构描述符“分子拓扑指数”(即舒尔茨指数)。Klavžar和Gutman在文献 [4] 中定义了修改舒尔茨指数。文献 [5] - [10] 研究和计算了舒尔茨指数和修改的舒尔茨指数。其他关于拓扑指数计算以及在化学工程中的应用可参考文献 [11] - [20] 。
多环芳香烃(Polycyclic Aromatic Hydrocarbons,简称PAH或PAHs)又称多环性芳香化合物或多环芳香族碳氢化合物,是芳香族碳氢化合物的一种特例。由不包含杂环或取代基的芳香环所组成。第一类多环芳香烃简称PAH1,是多环芳香烃家族的第一个成员,俗称苯环,如图1所示。
苯环是由6个sp2杂化碳原子通过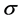 键和
键和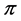 键构成平面正六边形的碳环,分子式为C6H6,苯环是最简单的芳香烃环,由六个碳原子构成一个六元环,每个碳原子接一个基团,苯的6个基团都是氢原子。
键构成平面正六边形的碳环,分子式为C6H6,苯环是最简单的芳香烃环,由六个碳原子构成一个六元环,每个碳原子接一个基团,苯的6个基团都是氢原子。
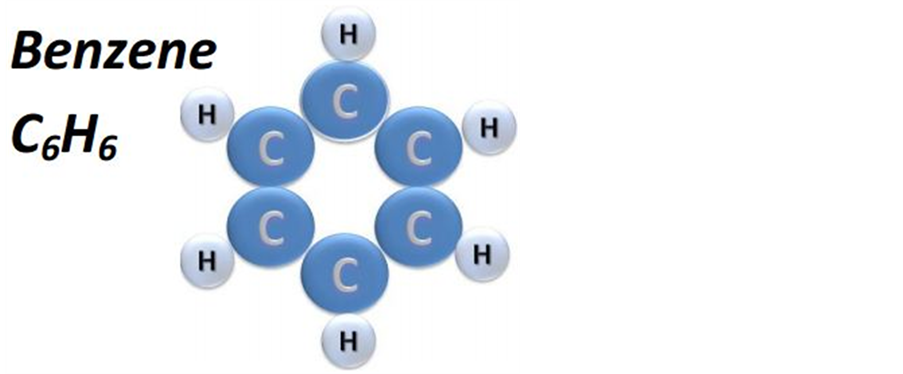
Figure 1. First member of polycyclic aromatic hydrocarbons
图1. 第一类多环芳香烃
苯分子中6个碳原子各以3个sp2杂化轨道分别跟相邻的两个碳原子的sp2杂化轨道和氢原子的1s轨道重叠,形成6个碳碳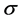 键和6个碳氢
键和6个碳氢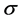 键。两个sp2杂化轨道的夹角是120˚,正适合6个碳原子处于一个平面上,形成一个正六边形的苯环。苯环上6个碳原子各有一个未杂化的2p轨道,6个2p轨道的对称轴都垂直于环的平面,并从侧面相互重叠,形成一个闭合的
键。两个sp2杂化轨道的夹角是120˚,正适合6个碳原子处于一个平面上,形成一个正六边形的苯环。苯环上6个碳原子各有一个未杂化的2p轨道,6个2p轨道的对称轴都垂直于环的平面,并从侧面相互重叠,形成一个闭合的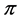 键。它均匀地对称分布在环平面的上方和下方。通常把苯的这种键型叫做大
键。它均匀地对称分布在环平面的上方和下方。通常把苯的这种键型叫做大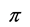 键。苯分子中
键。苯分子中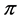 键电子云完全平均化,使苯环中每个碳碳键的键长和键能都是相等的。这就说明苯分子的对称性和稳定性。苯环的主要化学特性是环平面上下的
键电子云完全平均化,使苯环中每个碳碳键的键长和键能都是相等的。这就说明苯分子的对称性和稳定性。苯环的主要化学特性是环平面上下的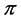 键电子容易受到亲电试剂的进攻,结果通常发生环上的取代反应。由于苯环较稳定,较难发生环上的加成反应。
键电子容易受到亲电试剂的进攻,结果通常发生环上的取代反应。由于苯环较稳定,较难发生环上的加成反应。
下面介绍本文关注的一些重要指数
一个分子图的顶点带权维纳数定义为:
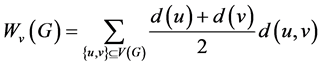 。
。
倒数度距离定义为:
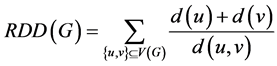 。
。
倒数乘法度距离定义为:
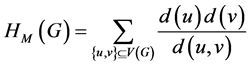 。
。
单顶点带权维纳多项式定义为:
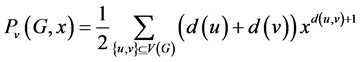 。
。
双顶点带权维纳多项式定义为:
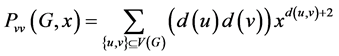 。
。
广义度距离定义为:
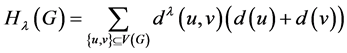 。
。
其中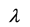 为实数。
为实数。
另外,修改的广义度距离则定义为:
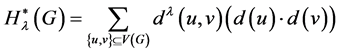 ,
,
其中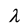 是实数
是实数
它们对应的多项式为:
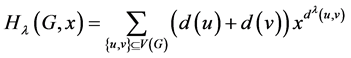 ,
,
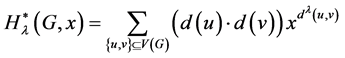 。
。
修改的维纳指数是原维纳指数的扩展,定义为
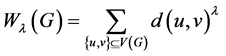 ,
,
其中 是非零实数。可见当
是非零实数。可见当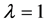 时,修改的维纳指数即为维纳指数。
时,修改的维纳指数即为维纳指数。
修改的超维纳指数是超维纳指数的扩展,定义为
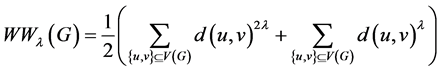 。
。
乘法维纳指数是维纳指数的另一种表现形式,定义为
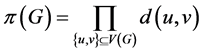 。
。
此外,对数乘法维纳指数定义为
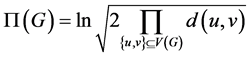 。
。
Harary指数是一类和维纳指数相关的指标,定义为
 。
。
对应的Harary多项式则定义为
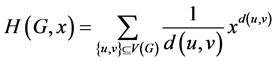 。
。
上述Harary指数通常称为第一类Harary指数,而第二类和第三类Harary指数则定义为
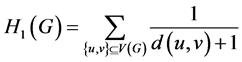 ,
,
 。
。
更一般地,广义Harary指数则定义为
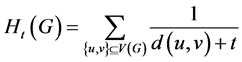 ,
,
其中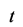 是一个非负整数。
是一个非负整数。
本文将给出第一类多环芳香烃的上述化学指数计算公式。
2. 主要结论及证明
设 为第一类多环芳香烃,它由6个碳原子(C)和6个氢原子(H)组成。假设
为第一类多环芳香烃,它由6个碳原子(C)和6个氢原子(H)组成。假设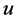 和
和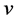 是分子图上的两个顶点,
是分子图上的两个顶点,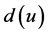 和
和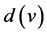 分别表示顶点
分别表示顶点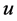 和
和 的度。设
的度。设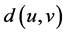 是分子图
是分子图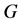 中顶点
中顶点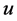 和
和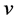 之间的最短距离。
之间的最短距离。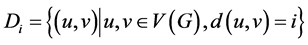 表示分子图中距离为
表示分子图中距离为 的顶点对的集合。顶点原子
的顶点对的集合。顶点原子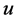 和
和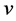 之间的最短路径的原子集合数为66,顶点之间的最短距离有从一到五一共五种。即
之间的最短路径的原子集合数为66,顶点之间的最短距离有从一到五一共五种。即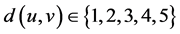 ,显然,
,显然,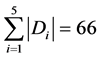 。下面,我们将把它分为五部分来一一列举。
。下面,我们将把它分为五部分来一一列举。
2.1. 顶点u和v之间最短距离为1
6个碳原子之间:
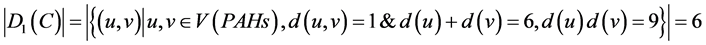 ,
,
则维纳多项式、广义舒尔茨多项式和广义修改的舒尔茨多项式中第一项的系数分别为6,36,54。
6个氢原子之间:
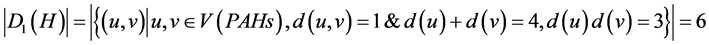 ,
,
则维纳多项式、广义舒尔茨多项式和广义修改的舒尔茨多项式中第一项的系数分别为6,24,18。
从整个分子图来看,第一项 ,
,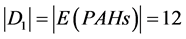 ,所以,维纳多项式、广义舒尔茨多项式和广义修改的舒尔茨多项式中第一项的系数分别为12,60,72。
,所以,维纳多项式、广义舒尔茨多项式和广义修改的舒尔茨多项式中第一项的系数分别为12,60,72。
2.2. 顶点u和v之间最短距离为2
6个碳原子之间:
 ,
,
则维纳多项式、广义舒尔茨多项式和广义修改的舒尔茨多项式中第一项的系数分别为12,72,108。
6个氢原子之间:
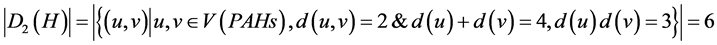 ,
,
则维纳多项式、广义舒尔茨多项式和广义修改的舒尔茨多项式中第一项的系数分别为6,24,18。
从整个分子图来看,第二项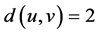 ,
,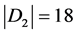 ,所以,维纳多项式、广义舒尔茨多项式和广义修改的舒尔茨多项式中第一项的系数分别为18,96,180。
,所以,维纳多项式、广义舒尔茨多项式和广义修改的舒尔茨多项式中第一项的系数分别为18,96,180。
2.3. 顶点u和v之间最短距离为3
6个碳原子之间:
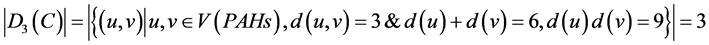 ,
,
则维纳多项式、广义舒尔茨多项式和广义修改的舒尔茨多项式中第一项的系数分别为3,18,27。
6个氢原子之间:
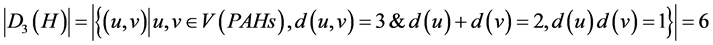 ,
,
则维纳多项式、广义舒尔茨多项式和广义修改的舒尔茨多项式中第一项的系数分别为6,12,6。
所有碳原子与氢原子之间:最短距离为3的顶点集合数为12。
从整个分子图来看,第三项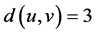 ,
,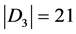 ,所以,维纳多项式、广义舒尔茨多项式和广义修改的舒尔茨多项式中第一项的系数分别为21,78,69。
,所以,维纳多项式、广义舒尔茨多项式和广义修改的舒尔茨多项式中第一项的系数分别为21,78,69。
2.4. 顶点u和v之间最短距离为4
6个碳原子之间:
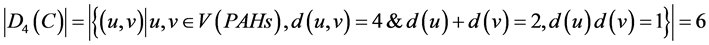 ,
,
则维纳多项式、广义舒尔茨多项式和广义修改的舒尔茨多项式中第一项的系数分别为6,12,6。
6个氢原子之间:
 ,
,
则维纳多项式、广义舒尔茨多项式和广义修改的舒尔茨多项式中第一项的系数分别为6,24,18。
从整个分子图来看,第四项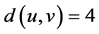 ,
,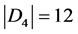 ,所以,维纳多项式、广义舒尔茨多项式和广义修改的舒尔茨多项式中第一项的系数分别为12,36,24。
,所以,维纳多项式、广义舒尔茨多项式和广义修改的舒尔茨多项式中第一项的系数分别为12,36,24。
2.5. 顶点u和v之间最短距离为5
从整个分子图来看,第五项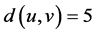 ,
,
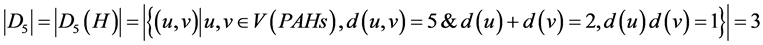 ,
,
所以,维纳多项式、广义舒尔茨多项式和广义修改的舒尔茨多项式中第一项的系数分别为3,6,3。
通过列举PAHs所有原子不同顶点之间的最短距离,可利用指数计算公式得到如下关于第一类多环芳香烃的指数计算公式。
顶点带权维纳数为:
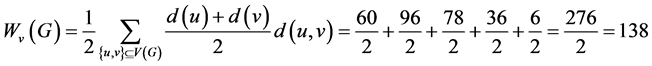 。
。
倒数度距离:
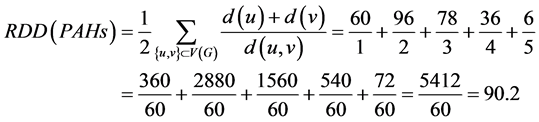
倒数乘法度距离为:
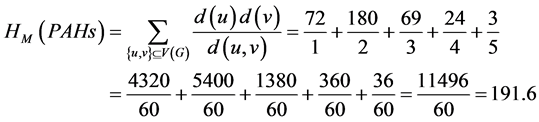
单顶点带权维纳多项式为:
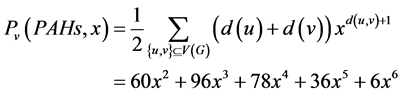
双顶点带权维纳多项式为:
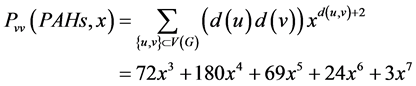
广义维纳指数为:
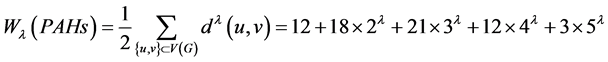
其中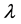 是实数。
是实数。
超维纳指数为:
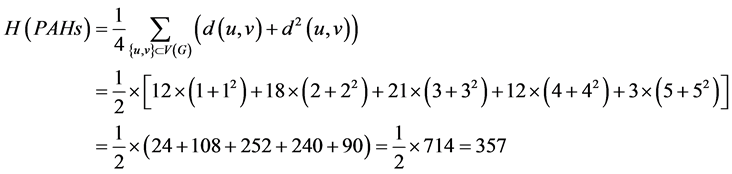 。
。
修改的超维纳指数为
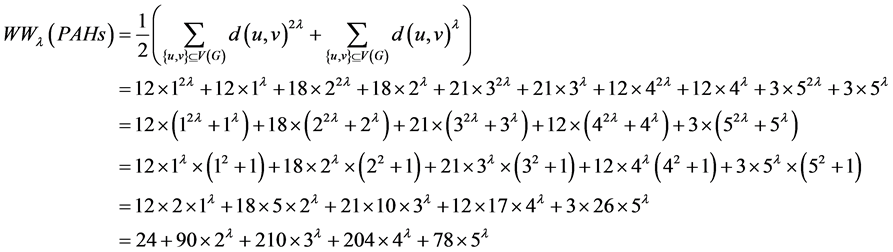 。
。
乘法维纳指数为
 。
。
对数乘法维纳指数为
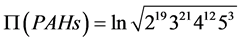 。
。
Harary指数是一类和维纳指数相关的指标为
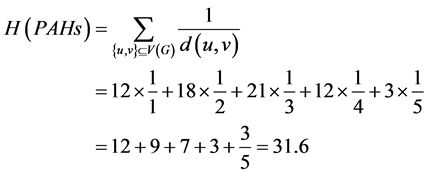
对应的Harary多项式为:
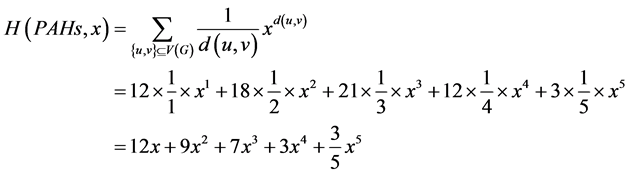
第二类Harary指数为:
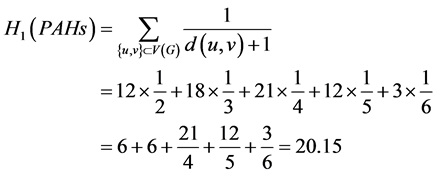 。
。
第三类Harary指数为:
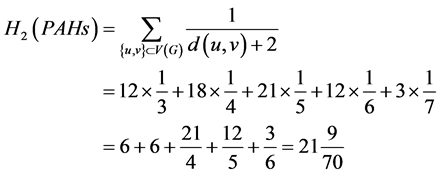 。
。
广义Harary指数为
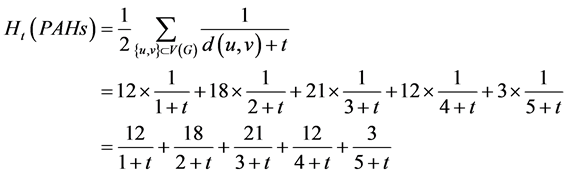 。
。
其中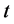 为非负整数。
为非负整数。
广义度距离和修改的广义度距离对应的多项式为:
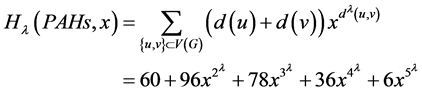 ,
,
 。
。
广义度距离为:
 。
。
修改的广义度距离为:
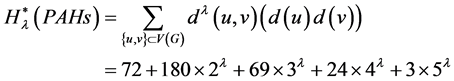
其中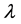 是实数。
是实数。
3. 总结
通过对第一类多环芳香烃的分子结构分析,可以计算出每一对顶点之间的距离,再根据指数计算公式得到相应的结果。本文理论结果可以为其它化合物的分析计算提供参考。