1. 引言
设计洪水是水利水电工程及流域规划工作防洪安全设计所依据的各种标准洪水的总称。合理确定设计洪水是江河流域规划和水利水电工程设计中的首要任务,它直接关系到江河开发治理的战略布局,关系着工程的规模、安全与经济社会效益,关系着人民生命财产的安全和社会的安定,因此,该问题历来都受到世界各国的重视。
无论在哪个国家,设计洪水的准确估算至关重要。在特定流域水文基础资料既定的条件下,设计洪水计算方法直接决定了设计洪水成果。世界各国流域水系结构、地形地貌、下垫面组成、气象条件、经济发展水平、水文水资源学科基础研究水平等各有不同,因而各国的设计洪水分析与计算不是统一的标准体系,而是最适合各国国情或水文特性的设计洪水体系。部分国家,如中国、英国、美国等,在长期的基础科研和工程设计实践基础上,形成了设计洪水计算的行业标准;部分国家没有制定统一的规范或标准,主要是基于实践应用经验或统计检验比较,例如,同一国家的不同区域可能会根据实际情况选择最适合的分布线型;也有一部分非洲国家,曾属英法等殖民地,直接采用殖民国的设计洪水计算方法。
为了使设计洪水成果符合区域要求,客观反映区域洪水特性,开展不同区域或国家设计洪水计算方法的比较研究,具有重要的理论意义和实际价值,可以有效指导国际水利水电工程项目的设计洪水计算。
2. 国内外设计洪水计算方法概述
2.1. 国内设计洪水计算方法概述
自1949年中华人民共和国成立至今的60多年内,我国已逐渐形成了一套比较完整的分析计算设计洪水的方法。1979年,原水利电力部颁发了《水利水电工程等级划分及洪水标准规范》(试行),这是中国第一次对水利水电工程设计所采用的洪水标准做出统一、明确的规定。1993年,对原试行规范修订后,水利部和能源部颁布了《水利水电工程设计洪水计算规范Sl44-93》。2006年,经再次修订后,水利部颁布了《水利水电工程设计洪水计算规范Sl44-2006》(下文简称《规范》) [1] ,该规范是我国目前水利水电工程洪水设计的重要依据。
中国水利水电工程设计洪水计算规范规定,洪水选样采用年最大值法,经验频率采用数学期望公式计算,洪水频率曲线的线型应采用P-III型(对特殊情况,经分析论证后也可采用其他线型),通过矩法(MM)或其他参数估计方法初步估算统计参数,采用适线法(CF)调整初步估算的统计参数。对用适线法确定的统计参数,还应该与本站洪峰、不同时段洪量统计参数,以及上游、下游、干支流和邻近流域各站统计参数进行合理性检查分析,必要时可作适当调整 [2] 。
2.2. 国外设计洪水计算方法概述
为了研究不同国家的设计洪计算方法,本文综述了各国标准协会、行业协会或相关水资源委员会发布的相关报告 [3] - [19] :
印度采用年最大值选样方法,选用Gumbel分布进行频率分析计算,通过矩法开展参数估计。
日本采用年最大值选样方法,根据拟合度来选择确定频率曲线,常用的频率曲线主要有三种:正态型分布,极值型分布和指数型分布。
马来西亚采用年最大值选样方法,经验频率公式建议采用数学期望公式,洪水频率曲线线型采用Gumbel分布,通过矩法估计Gumbel分布的参数。
澳大利亚洪水频率分析可以按照年最大值选样和超定量(POT)选样,经验频率公式采用Cunnane公式 [8] 。对年最大值选样系列,洪水频率曲线线型通常采用广义极值(GEV)分布和对数P-III (Log P-III)分布。对POT系列,洪水频率曲线线型通常采用指数分布、Generalized Pareto (GP)分布和Log P-III分布。采用线性矩法(LM)估计分布参数。
英国洪水频率分析通常可以按照年最大值选样和超定量选样,经验频率公式采用Gringorten公式。在英国规范中,频率分析首先由流量资料或流域特征值计算年最大洪水中值,然后采用Generalized Logistic (GL)分布进行洪水频率分析。统计模型参数估算采用线性矩法。当观测系列较短时,推荐采用洪水频率区域综合分析。
挪威洪水频率分析通常可以按照年最大值选样和超定量选样。经验频率公式采用Gringorten公式。Gumbel分布和GEV分布被发现与挪威的流域洪水资料吻合最好,但挪威的洪水频率估计指南建议最好选取多个分布,比较哪个最适合来选取最佳。现有的参数估计方法有矩法、线性矩法和最大似然估计法,其中线性矩法是最常用的方法之一。
法国可以采用年最大值选样和超定量选样,推荐采用年最大值选样方法。经验频率公式建议采用中值公式。洪水频率曲线线型通常采用GEV分布。采用线性矩法估计分布参数。
西班牙一般采用年最大值选样方法。经验频率公式建议采用Gringorten公式。洪水频率曲线线型绝大多数采用GEV分布,只有极少数为Gumbel分布。采用线性矩法估计GEV分布的参数。均值和线性矩变差系数L-CV采用该站点自身的计算值,线性矩偏态系数L-CS则采用区域值。
瑞典采用年最大值选样方法,频率分布有Gumbel分布、Log P-III分布和对数正态分布等。采用矩法估计参数,采用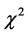 分布来选择最适合的线型。
分布来选择最适合的线型。
俄罗斯一般采用年最大值选样方法,经验频率公式采用中值公式或数学期望公式。频率曲线采用克里茨基-闵开里(K-M)分布。分布参数求解非常复杂,一般只能得到数值解。
德国一般采用年最大值选样方法,洪水频率曲线线型通常采用GEV分布,采用线性矩法估计GEV分布的三个参数。
美国采用年最大值选样方法,频率分析选用Log P-Ⅲ型分布,采用矩法估计统计模型参数。当站点洪水样本系列小于100年时,偏态系数Cs由站点估计值和Cs区域值加权计算。
加拿大可采用年最大值和超定量两种取样方法。水文频率线型可以采用正态分布、对数正态分布、三参数对数正态分布、极值I型分布、极值II型分布、极值III型分布、P-III分布和Log P-III分布。参数估计的主要方法有矩法和极大似然法。
2.3. 方法比较与评价
通过对各国设计洪水计算方法进行分析,可以得出以下结论:
1) 世界各国基于频率分析推求设计洪水,技术思路基本一致,主要在数据选样、经验频率公式、频率曲线分布线型、参数估计方法等方面存在差异。
2) 在基于流量资料推求设计洪水时,通过构建洪水频率分析模型来进行计算,该模型由洪水频率分布函数和参数估计方法构成。一般根据各国的规范或者实际情况选择水文变量最适合的分布函数后,采用合理的参数估计方法求解该分布函数的各项参数,从而得到水文变量的理论分布函数,并通过它进行设计洪水计算。
3) 对于设计洪水计算方法是推荐方式,部分国家,如中国、美国、英国等,基于专业基础研究和大量工程应用实践,以行业规范、推荐指南、计算手册的形式推荐,权威性和强制性较高;部分国家以协会、水资源委员会或理事会发布的报告形式予以推荐;还有些国家没有明确的洪水计算规范或指南性文件,常用的设计洪水计算方法均可接受。
4) 据现有参考文献分析,各国洪水系列选样方法以年最大值选样居多,有一部分国家年最大值与超定量选样均可,如加拿大、英国、挪威、澳大利亚等。中国《规范》推荐采用年最大值选样,并规定洪水系列长度一般要有30年。
5) 各国采用的洪水频率曲线线型,均为水文领域常见的几种分布函数,如P-III分布,Log P-III分布,GEV分布,Gumbel分布,正态分布,对数正态分布,GL、K-M分布等。各国在做频率线型推荐时,部分选择与本国洪水资料拟合最好的某一种线型,部分允许采用多种线型,以统计拟合优度检验来确定最终的线型。中国以规范的形式,推荐采用与我国南北地区洪水资料系列拟合均较好的P-Ⅲ分布,特殊情况,经充分论证,也可采用其它线型。
6) 对于参数估计方法,采用线性矩法或矩法的居多。大多数国家,在设计洪水计算过程中,依据洪水样本系列和一定的参数估计方法计算分布函数的参数值,计算的参数值即为最终的参数值,不再做调整。中国《规范》推荐采用矩法等方法计算的参数值作为初估值,经验适线法确定最终的参数值。该方法主要是考虑在确定稀遇洪水频率时,在理论分布曲线与经验点距拟合过程中,根据工程设计专业人员的经验,给予洪水系列样本中的历史调查大洪水或实测系列中的大洪水予以更多的关注和权重。
3. 洪水频率分析模型
3.1. P-III/CF洪水频率分析模型
如前文所述,中国《规范》推荐采用P-III型分布和目估适线(Curve Fitting)法确定参数,简记为P-III/CF洪水频率分析模型。P-III分布函数的概率密度函数为:
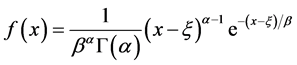 (1)
(1)
式中: 、
、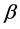 和
和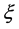 分别为分布的形状、尺度和位置参数。
分别为分布的形状、尺度和位置参数。
在做频率分析前,应先做系列代表性分析,以了解洪水频率计算所依据的样本系列是比较合适、还是可能偏大或偏小,以便帮助我们在推求设计洪水的各个步骤中及设计洪水数值的最终选用时做出正确的判断,减少对工程防洪设计带来的不安全的因素。
连序系列一般指由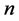 年实测(包括插补延长)资料组成的系列,其各年洪水的经验频率可采用数学期望公式计算,即
年实测(包括插补延长)资料组成的系列,其各年洪水的经验频率可采用数学期望公式计算,即
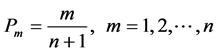 (2)
(2)
式中: 是
是 年连序系列中按由大到小顺序排列,其序位为
年连序系列中按由大到小顺序排列,其序位为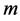 的洪水经验频率。
的洪水经验频率。
不连序系列指由历史调查洪水、实测系列中洪水的特大值以及其余的实测洪水系列混合组成的系列。对于不连序系列,如在历史洪水的调查考证期 年中已调查到前
年中已调查到前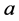 个洪水,其中有
个洪水,其中有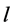 个是发生在
个是发生在 年实测系列中,则这类不连序系列的经验频率可以采用统一样本法和独立样本法计算,其中统一样本法的计算公式如下:
年实测系列中,则这类不连序系列的经验频率可以采用统一样本法和独立样本法计算,其中统一样本法的计算公式如下:
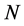 年中前
年中前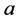 个洪水的经验频率为
个洪水的经验频率为
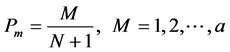 (3)
(3)
实测系列中除特大值外的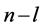 个洪水的经验频率为
个洪水的经验频率为
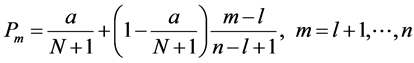 (4)
(4)
3.2. P-III/LM洪水频率分析模型
该模型采用P-III线型作为频率分布函数,通过线性矩法估计参数。P-III分布函数的各项参数和常规矩统计参数的关系为:
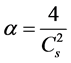 ,
, ,
, (5)
(5)
式中: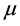 、
、 和
和 分别为均值、均方差和偏态系数。
分别为均值、均方差和偏态系数。
线性矩法 [20] 起源于概率权重矩,是概率权重矩的线性组合。样本线性矩:假定观测到变量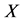 的
的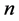 个样本值,将其按从小到大的顺序进行排列。用
个样本值,将其按从小到大的顺序进行排列。用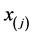 表示样本序列中排序为
表示样本序列中排序为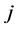 的值,前三阶样本线性矩计算如下
的值,前三阶样本线性矩计算如下
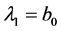 ,
, ,
,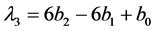 (6)
(6)
其中:
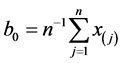 ,
, ,
,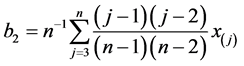 (7)
(7)
P-III型分布的一阶线性矩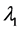 、二阶线性矩
、二阶线性矩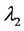 、三阶线性矩
、三阶线性矩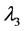 和线性变差系数
和线性变差系数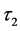 、线性偏态系数
、线性偏态系数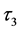 分别可用以下公式表示:
分别可用以下公式表示:
 ,
, (8)
(8)
根据线性矩估计P-III型分布三个统计参数的计算方法如下:
当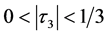 时,令
时,令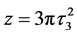 ,
,
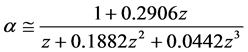 (9)
(9)
当 时,令
时,令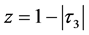 ,
,
 (10)
(10)
则三个统计参数计算公式如下:
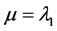 ;
; ;
; (11)
(11)
对于具有历史洪水信息的非连续样本,考虑到线性矩是概率权重矩的线性组合,则其线性矩公式不变,只需要将此时的概率权重矩公式改为具有历史洪水时的样本概率权重矩公式。
3.3. Gumbel/LM洪水频率分析模型
该模型采用Gumbel分布作为频率线型,通过线性矩法估计参数。GEV分布的概率密度函数式为:
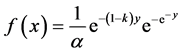 (12)
(12)
其中:
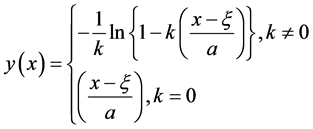 (13)
(13)
式中: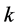 、
、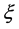 和
和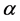 分别为形状、位置和尺度参数。当
分别为形状、位置和尺度参数。当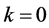 时,GEV分布即为Gumbel分布。
时,GEV分布即为Gumbel分布。
Gumbel分布与线性矩之间的关系式如下:
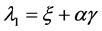 ,
,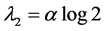 (14)
(14)
其中, 为欧拉常数,等于0.5772,则参数
为欧拉常数,等于0.5772,则参数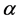 、
、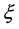 的计算公式如下
的计算公式如下
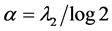 ,
,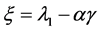 (15)
(15)
3.4. Log P-III/MM洪水频率分析模型
该模型采用的分布函数为Log P-Ⅲ线型,该分布是将对应超过概率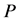 的年峰值流量
的年峰值流量 取以10为底的对数,则有公式:
取以10为底的对数,则有公式:
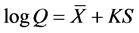 (16)
(16)
式中: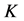 是频率因子,均值
是频率因子,均值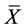 、标准差 和对数偏态系数G定义如下:
、标准差 和对数偏态系数G定义如下:
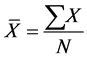 (17)
(17)
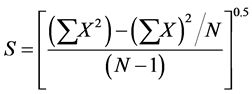 (18)
(18)
 (19)
(19)
 (20)
(20)
式中: 为年峰值流量取对数;
为年峰值流量取对数;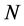 为连序序列长度;
为连序序列长度; 为流量取对数后的均值;
为流量取对数后的均值;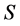 为流量取对数后的标准差;
为流量取对数后的标准差; 为取对数后的偏态系数;
为取对数后的偏态系数;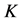 为超过概率
为超过概率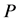 和对数偏态系数
和对数偏态系数 的函数,可根据查表得到。
的函数,可根据查表得到。
4. 设计洪水计算方法的比较研究
4.1. 计算方案及成果
以国外某水库为实例,坝址处没有设立水文站,坝址上游水文站具有1956~2009年共54年实测洪水系列,并调查有两场历史洪水,坝址下游水文站具有1971~2009年(缺测1年)共38年实测洪水系列,无历史洪水。结合流域暴雨洪水特性分析,宜采用上下游水文站为设计依据站,按照面积比内插推求坝址设计洪水。
分别构建P-III/CF、P-III/LM、Gumbel/LM和Log P-III/MM四种洪水频率分析模型,分别对坝址的设计依据站(上游和下游水文站)进行设计洪水计算,然后通过面积比内插推求坝址设计洪水成果,如表1所示。
4.2. 成果分析与讨论
对比前期设计洪水成果和本次四种洪水频率分析模型得到的坝址洪水设计值,可以得出以下结论:
1) 前期设计洪水成果明显偏小,主要原因是采用的设计依据站的代表性不足,且实测资料序列太短。前期设计时,仅采用下游水文站作为坝址设计依据站,本次还采用了上游水文站作为设计依据站,上游水文站的资料精度明显高于下游水文站。前期设计时,仅采用了下游水文站共20年的洪水实测资料,本次采用了38年的洪水资料;通过分析洪水系列,发现该水文站的最大五场洪水均发生在本次系列延长之后。本次研究依据上下游站的设计洪水成果内插计算坝址设计洪水,比较符合区域洪水特性的实际情况。
2) 采用P-III/LM模型得到的稀遇洪峰设计值比采用P-III/CF的计算结果偏小。P-III/LM比P-III/CF洪水频率模型估计的万年一遇、五千年一遇洪峰设计值分别偏小14.1%、13.5%;万年一遇3 d洪量,7 d洪量和15 d

Table 1. Results of design flood estimated by different flood frequency analysis models
表1. 不同洪水频率分析模型的坝址设计洪水成果(单位:洪峰,m3/s;洪量,108 m3)
洪量设计值分别偏小14.6%,15.2%和12.8%。
3) Gumbel/LM、Log P-III/MM两种模型的稀遇洪峰设计值均比P-III/CF的设计值小。其中,Gumbel/LM、Log P-III/MM模型估计的万年一遇设计洪水分别比P-III/CF的设计值偏小6.3%和4.8%。对于洪量设计值,Gumbel/LM模型估计的万年一遇、五千年一遇3 d洪量设计值比P-III/CF的设计值稍有偏小,7 d洪量和15 d洪量设计值比P-III/CF的设计值略大;Log P-III/MM模型估计的万年一遇、五千年一遇不同时段洪量设计值比P-III/CF偏小6.9%~12.5%。
4) 不同频率分析模型得到的坝址设计洪水成果基本在同一个量级,各种模型的成果差异,跟模型构建中的频率分布线型选择、参数估计方法有关,也跟适线准则有关。在P-III/CF模型中,面向稀遇设计洪水的推求目的,重点考虑洪水样本系列中的历史调查大洪水和实测大洪水拟合情况,调整参数初值,确定了最终参数值。
5) 历史洪水资料具有两面性。一方面,在现有资料系列样本较短的现实情形下,希望尽量利用历史洪水资料,提高短期洪水样本系列的代表性,得到较为正确的总体分布。如果历史洪水的量值及其重现期能有较为可靠的考证和推求,则频率曲线的外延指导会较为可靠,历史洪水资料的利用就是一种有效的提高代表性的措施。另一方面,种种因素综合作用下,历史调查洪水峰值易于高估,重现期易于低估,若估计误差太大,则有可能损害系列的代表性。
6) 设计洪水是个科学难题。在很多情况下,设计洪水是一种高度困难的推求极值问题,无论中外,在水利水电工程领域,多需要根据有限的几十年洪水样本资料推求可能发生的几百年、甚至千年、万年一遇的洪水情况。因为洪水事件带有随机性,是一种概率问题,因此应用概率论和数理统计来进行洪水频率计算是常见的研究手段。数理统计的前提要求是大样本,而洪水问题往往只有小样本,即使偶有系列达百余年,性质上也还是小样本,因而设计洪水注定是高难度的科学问题。
7) 洪水的总体分布是未知的。洪水现象是高度复杂的多因素复合自然现象,其必然性规律无法确切得知,其统计规律也难于从目前的较短实测水文系列肯定地推求。因此,人们只能基于假定分布函数与实测洪水系列的拟合情况,来选出能够较好的拟合大多数水文站点较长实测洪水系列的线型作为最优线型。在具体设计问题中,应结合项目所属地区的行业领域研究情况,辩证的分析,合理地选择洪水分布函数。
5. 结论
本文介绍了国内外基于流量资料推求设计洪水的计算方法及频率洪水分析中常用的几种洪水频率分析模型。以国外某水库为实例,分别建立了P-III/CF、P-III/LM、Gumbel/LM和Log P-III/MM四种洪水频率分析模型,开展了设计洪水计算方法的比较研究。研究表明:
1) 在开展洪水设计时,样本资料系列的代表性非常重要,同时也要认识到历史洪水具有可能提高样本资料代表性和可能损害系列代表性的两面性。
2) 不同洪水频率分析模型的成果差异,跟模型构建中的频率分布线型选择、参数估计方法有关,也与适线准则有关。经验适线法在根据一定的参数估计方法确定初值的基础上,会较为重视高水点据特别是可靠的历史洪水点据来调整参数,外延频率曲线来推求极值,是P-III/CF模型稀遇设计洪水成果较其它模型成果偏大的原因之一。
3) 基于设计洪水科技问题中存在的各种客观现实条件,在开展洪水研究和设计中,应客观审慎,充分重视基础资料的“三性”分析及过程和成果的合理性分析。
基金项目
国家自然科学基金资助项目(51539009)。