1. 引言
近年来，供应链管理成为一个重要的学术和商业问题，引起广泛的关注。随着科技和经济的迅猛发展，市场中产品生命周期不断缩短，需求瞬息万变，企业开始重视对供应链的管理，围绕买卖双方间的物流和资金流实施信息共享和经营协调，以实现稳定、高效、柔性的供需关系、使供应链中的成员获得相应利益。随着供应链系统的日趋复杂以及外界环境的不确定性逐渐增加，对供应链管理的建模、优化、仿真已经成为研究供应链管理的有力工具。
供应链的绩效评价与决策是研究供应链管理的一个关键问题。霍佳震 [1] 等建立起系统的供应链绩效评价指标体系、综合评价供应链整体绩效和各子系统的绩效；曹晓刚 [2] 等研究了在非对称信息和模糊需求下，由单一制造商和零售商组成的闭环供应链系统的协调问题。从前人的研究来看，大部分是从建立评价指标体系入手，然后采用层次分析、模糊评价、主成分分析等方法进行分析，很少使用运筹与最优化方法建立供应链决策模型。
供应链不确定性 [3] 是研究供应链管理的又一个问题，供应链不确定性影响了供应链绩效，是引起供应链管理复杂性和困难性的主要原因之一。从目前的研究看，孙浩等研究了随机环境下考虑需求替代的闭环供应链决策模型 [4] ，针对制造商和零售商的利润最大化进行决策；徐家旺 [5] 等建立了价格与需求不确定条件下供应链运作的多目标模糊规划模型。大部分研究都是考虑由制造商和零售商组成的二层供应链系统，且仅讨论在市场供求不确定情况下的供应链运作模型。
针对上文提到的两个问题，本文考虑由单一供应商和单一制造商构成的供应链系统 [6] ，使用运筹与最优化的方法建立起随机环境下的供应链多目标决策模型，利用模型分别讨论了原材料市场与消费市场均无限制、单一市场不确定以及两市场供求均不确定三种情形 [3] 下的供应链的运作情况，结合鲁棒线性优化方法 [7] 建立了随机环境下的供应链的多目标鲁棒决策模型。
2. 问题描述和模型假设
2.1. 问题描述
考虑由一个供应商和制造商构成的两层多阶段供应链决策系统，生产和销售短生命周期的多种产品。在这个系统中，生产商负责原材料的加工和原料的生产，制造商负责产品的生产和销售，供应链成员之间的关系 [4] 如图1所示。假设供应商面对的原材料市场的供应量和制造商面对的消费市场的需求量在各阶段均是随机的，即原材料市场和消费市场均无限制、消费市场需求不确定、原材料市场供应不确定和原材料市场供应与消费市场需求均不确定这四种情形均可能发生，建立此情形下的供应链决策模型。
2.2. 模型假设
1) 假设在供应链在运作过程中，供应商的交付量与制造商的订购量相等；
2) 制造商和供应商均为风险中性决策者，均以实现企业利润收益最大化为目标；
3) 假设在每一阶段内，市场的供应量和需求量为一定值；
4) 假设在供应链在运作过程中，供应链的利润最大化为第一优先因子 [6] ，各阶段供应商的支付量与制造商的订购量的平衡关系为第二优先因子，且由于市场的供需情况不确定，在建立供应链运作模型时，假设供应商和制造商的期望利润的优先级相同的页边距不被修改，页面空白不被占用。
2.3. 符号说明
i为制造商的生产原料
；j为制造商的最终产品；t为时间阶段
；h为供应商的原材料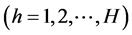
。
决策变量
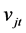为最终产品j在t阶段的销售量；
为最终产品j在t阶段的生产量；
为最终产品j在t阶段的库存；
为制造商的原料i在t阶段的库存；
为制造商在t阶段对原料i的订货量；
为供应商在t阶段对原料i的交付量；
为供应商在t阶段对原料i的生产量；
为供应商在t阶段对原料i的库存。
参数
为t阶段最终产品j的价格；
为t阶段原料i的价格；
为最终产品j的可单位制造成本；
为最终产品j的单位库存成本；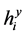
为制造商原料i的单位库存成本；
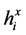为供应商原料i的单位库存成本；
为最终产品j的生产能力消费率；
为供应商原料i的生产能力消费率；
和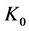
分别为制造商的附加生产能力率和附加生产能力；
和
分别为供应商的附加生产能力率和附加生产能力；
为制造商可利用的最大生产能力；
为供应商可利用的最大生产能力；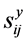
为最终产品j对原料i的BOM系数；
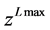为最终产品的总库存能力；
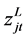为最终产品在t阶段的库存；
为最终产品j的初始库存；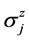
为单位最终产品j在制造商处所占的库存；
为原料总库存能力；
为生产原料i在制造商处的初始库存；
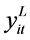为生产原料i在t阶段的库存；
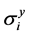为单位生产原料i在制造商处所占的库存；
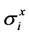为单位原料i在供应商处所占用的库存；
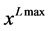为原材料的总库存能力；
为t阶段原材料h的价格；
为供应商生产原料i的
Figure 1. The relationship between the members of a supply chain
图1. 供应链成员关系图
单位可变成本；
为原料i对原材料h的BOM系数；
为供应商原料i的单位库存成本。
3. 多产品、多阶段供应链的多目标规划模型
在供应链的运作过程中，供应商以追求利润最大化为目标，以此决定各阶段向制造商的交付产品的数量；制造商也以追求利润最大化为目标，在此条件下决定各阶段向供应商订购生产原料的数量。本文首先研究了单一制造商和单一供应商各自的运作模型。
3.1. 单一制造商运作模型
制造商追求利润最大化，即目标函数为
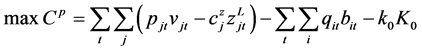(1)
其中，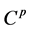
为制造商的实际利润。
约束条件：
1) 各阶段生产能力约束：
(2)
2) 各阶段最终产品库存约束：
(3)
3) 各阶段制造商原料库存约束：
(4)
4) 消费市场需求不稳定性约束:
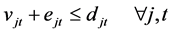(5)
其中，
为t阶段消费市场对最终产品j的需求量
5) 实际订购约束：
(6)
6) 生产约束：
(7)
3.2. 单一供应商运作模型
供应商追求利润最大化，即目标函数为
(8)
其中，
为供应商的实际利润。
1) 各阶段生产能力约束：
(9)
2) 供应商产品库存约束：
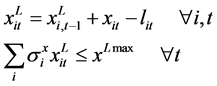(10)
3) 原材料市场供应不确定约束：
(11)
其中，
为t阶段供应商从原材料市场所能获得的原材料数量。
4) 实际交付约束：
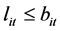(12)
5) 生产约束：
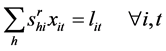(13)
3.3. 供应链多目标优化模型
供应链整体正常运作的每个阶段，供应链成员之间的运作是协调的，即供应商和制造商的订购量和交付量是相等的。在此基础上，供应链双方面对不确定的市场来确定自己的最优运作策略，制造商面对不确定的消费市场追求利润最大化，供应商在供应链协调运作基础上追求最高收益。
结合已建立的制造商运作模型和供应商运作模型，在图1的供应链中，考虑一下三个目标：
1) 供应链协调运作条件
供应链协调运作，即供应商的交付量等于制造商的订购量，模型可以表示为：
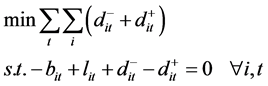(14)
其中，
和
分别为供应商在t阶段对制造商所需的第i种原料的不足交付量和过剩交付量。
2) 制造商追求目标利润的最大化
制造商通过调整生产原料的订购量和最终产品的销售量来追求利润的最大化，其模型可以表示为
(15)
约束条件为(2)~(7)，该规划等价于目标规划：
(16)
同时还受到(2)~(7)的约束。其中，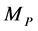
为制造商的期望利润，是一个给定的常数；
为制造商的实际利润；
和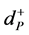
分别为制造商期望利润的不足值和过剩值；
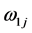为产品j的需求量每减少一个单位给制造商带来的利润损失；
为制造商在t阶段未满足的市场需求量。
3) 供应商追求目标利润的最大化
供应商通过调整原材料的购买量和生产原料的支付量来追求利润最大化，其目标函数为
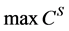(17)
约束条件为(9)~(13),该线性规划等价于目标规划
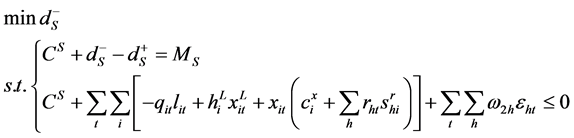(18)
其中，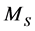
为供应商的期望利润，是一个给定的常数；
为供应商的实际利润；
和
分别为供应商期望利润的不足值和过剩值；
为原材料h的供应量每减少一个单位给供应商带来的利润损失；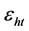
为原材料市场供应原材料的不足量。
基于文中关于供应链各成员优先级的假设，假定供应商与制造商两者期望利润的优先级相等，定义两者的期望利润的优先因子为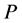
，同时定义描述供应链运作协调性的目标函数的优先因子为
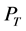，且
。因此，多阶段供应链的多目标规划模型可以表示为：
(19)
基本约束条件为(16)和(18)，另外还有对供应商和制造商的生产能力、产品库存、实际生产、实际销售的约束条件为(2)~(7)和(9)~(13)，以及非负条件：
(20)
4. 随机环境下的供应链多目标鲁棒决策模型
为了研究随机环境下供应链的运作情况，本文分别从原材料市场和消费市场均无限制、消费市场需求不确定、原材料市场供应不确定和原材料市场供应与消费市场需求均不确定这四种情形 [7] 建立供应链决策模型。
4.1. 两市场均无限制
考虑原材料市场供应充足并且消费需求很大，制造商生产的最终产品都能卖出去的情形下供应链的运行情况。此时，对于制造商，其产品的销售量没有限制，即没有消费市场需求不确定约束(5)；对于供应商，其原材料市场的供应不确定约束(12)也不起作用。综上，供应链运作的多目标规划模型简化为：
约束条件为(2)、(3)、(4)、(6)、(7)、(9)、(10)、(11)、(12)和(20)。
此时考虑单独的供应商和制造商的运作模型，供应商运作规划模型不含制造商模型中的决策变量，因此可以采用两次线性规划的求解方法，先求解供应商的交付量，再求解制造商的订购量，从而求解上述多目标线性规划问题。
4.2. 单一市场不确定
考虑原材料市场的供应量没有限制但消费市场的需求量不确定和消费市场的需求没有限制但原材料市场的供应量不确定两种情形下供应链的运作情况。这里仅分析情况一下的情形，情况二与情况一类似。
情况一下，供应商的生产不受原材料市场供应的影响，即多目标规划中不受原材料市场供应不确定约束(12)的作用，供应商的支付量依赖于制造商的订购量。在以上多目标规划中，供应商运作规划模型中不包含制造商模型中的决策变量，因此也可用两次线性规划方法求出整个多目标规划模型的解。
4.3. 两市场均不确定
两市场均不确定时，制造商向市场销售的产品量受到消费需求的限制，同时供应商的生产还受到原材料市场的供应量的限制。本文引入概率模型 [5] ，利用已知概率的离散情景来描述市场供求的不确定情形，利用鲁棒线性优化 [8] 的方法将多目标优化线性化，最终建立基于离散概率模型的多目标鲁棒决策模型来描述供应链的运作情况。
设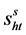
和
分别表示情形s下原材料的供应量和最终产品的需求量，
和
表示对应于情景s的供应商生产量和制造商销售量，
为制造商在t阶段未满足的市场需求量，
为原材料市场供应原材料的不足量，其他参数在不同情形下不变。用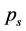
表示情形s发生的概率，则供应链运作的多目标规划模型可以表示为：
(21)
该规划还应满足约束(2)~(7)和 (9)~(13)，以及非负条件(20)。
采用基于区间分析的鲁棒线性优化方法，在原材料供应和最终产品需求均不确定环境下，供应链运作的多目标规划模型的所有约束条件均是线性的。因此，可以利用Lingo对上述多目标线性规划进行求解。
5. 算例验证
考虑只有一种原材料(
)、一种中间生产原料(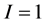
)、一种最终产品(
)和2个运作阶段(
)的简单情形 [9] 。假定：在2个运作阶段，原材料价格分别为30，35，最终产品的价格分别为80，85；各阶段供应商均以50的销售价格向制造商供应生产原料，其他参数分别给定如下：
。
根据以上参数，以下利用Lingo12建模软件分别求解原材料供应充足但最终产品需求不确定以及两市场均不确定两种情形下供应链的运作决策模型。
5.1. 情形1：原材料供应充足但最终产品需求不确定
供应商和制造商的运作策略如表1所示。
Table 1. The optimal operation strategy of case 1
表1. 情形1下的最优运作策略
Table 2. The optimal operation strategy of case 2
表2. 情形2下的最优运作策略
从表1可以看出，在两个运作阶段，制造商的生产原料订购量与供应商交付量均相等，即供应链运作协调性目标实现，同时消费市场最终产品的需求得到满足。
5.2. 情形2：两市场均不确定
两市场供应与需求均不确定下，不确定性的伸缩度为5时，供应商和制造商的运作策略如表2所示。
从表2可知，在原料市场原材料供应和消费市场最终产品需求不确定性的伸缩度均为5时，两个阶段制造商的生产原料订购量与供应商交付量均相等，供应链运作的协调性满足，但与情形1相比，两者的运作策略发生变化，且利润也有所变化，但变化幅度比较小，这也反映了模型具有较好的鲁棒性和稳定性。
6. 结语
本文考虑了一个由单一供应商和单一制造商构成的多产品、多阶段供应链系统在随机环境下的运作情况。供应链的运作追求供应链成员之间的协调性、集成供应链各成员利润最大化以及运作策略的鲁棒性三个目标达到最大化。首先使用运筹与最优化的方法分别描述供应商和制造商的运作情况，建立了多产品、多阶段供应链运作的多目标决策模型；其次，分别讨论了原材料市场与消费市场均无限制、单一市场不确定以及两市场均不确定三种情形下，供应链的运作情况，建立了随机环境下基于离散概率模型的多目标鲁棒决策模型；最后，设计数值算例对模型的可行性和鲁棒性进行验证，算例结果表明，本文提出的供应链决策模型可以准确计算出各阶段制造商原料的订购量和供应商产品的支付量，为供应链的协调运作提供决策。
基金项目
国家自然科学基金资助项目(71271171)；大学生创新训练项目(201510699231)。