1. 引言
一个注水开发油田,需要通过注水以保证油井具有旺盛的生产能力,一般是通过注采平衡来达到较好的开发效果,要实现注采平衡就必须有一个合理的注采比 [1] - [4] 。油田在长期注水开发之后,不可避免地会产生无效注水,造成油田开发的恶性循环 [5] [6] 。无效注水是指没有作用到水驱采油的那部分注水量,一般通过理论方法确定,比如甲型水驱特征曲线法 [7] ,但是由于油田地质情况的复杂和开发情况的多样性,通过一般的理论方法,某一时刻的无效注水比例是难确定的。
本文以物质平衡原理与Logistic旋回理论为基础进行了理论推导,得到了考虑无效注水的合理注采比的确定方法,最终确定出无效注水比例。基于实际Z油田的生产数据,对该油田的合理注采比进行了计算,并与应用油藏数值模拟方法确定出的Z油田的合理注采比进行了对比,从而验证此方法的正确性,说明此方法能很好的为油田后续的注水开发提供理论指导依据。
2. 考虑无效注水的合理注采比理论推导
该理论推导的基本思路是:首先应用物质平衡原理,确定油田压力恢复速度与考虑无效注水的注采比、注水量的关系,然后以Logistic旋回理论为依据,根据油田或油田不同含水时产油量与注水量之间的定量关系,就可以得到不同含水时压力恢复速度与注采比、采油量的关系,最终就可以确定出合理注采比。
在油田注水条件下,由物质平衡原理 [8] ,可得:
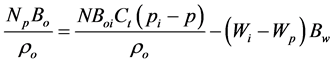 (1)
(1)
式中:N——地质储量,104 t;
Np——累计产油量,104 t;
pi——原始地层压力,MPa;
p——目前地层压力,MPa;
ρo——地面脱气原油密度,kg/m3;
Ct——油层综合压缩系数,1/MPa;
Boi——原始原油体积系数;
Bo——目前原油体积系数;
Bw——地层水体积系数;
Wi——累计注水量,104 m3;
Wp——累计产水量,104 m3。
当地层压力的变化保持在很小的范围内,把原油体积系数看作一个常数,同时考虑油田无效注水等因素的影响,最终求得年压力恢复速度与注采比、年注水量的关系为:
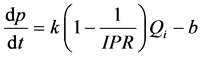 (2)
(2)
式中:k——与地质储量、岩石及地下流体性质有关的常数;
b——无效注水对压力恢复速度的影响系数,线性回归得到,MPa/a。
Logistic旋回的数学模型 [9] 为:
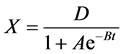 (3)
(3)
式中:X——体系;
t——体系的发展过程或时间;
D——生命过程的经验常数;
A,B——拟合系数。
旋回模型表示体系从兴起发展到X为  的过程。
的过程。
由于水驱开发油田的含水率随着生产时间的延长逐渐上升,且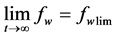 ,因此可用Logistic旋回模型建立起综合含水率与累计耗水量和累计水油比的定量关系为:
,因此可用Logistic旋回模型建立起综合含水率与累计耗水量和累计水油比的定量关系为:
 (4)
(4)
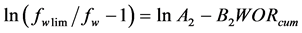 (5)
(5)
式中:fw——综合含水率;
fwlim——极限综合含水率,一般取值为0.98;
Wi——累计注水量,104 m3;
Wp——累计产水量,104 m3;
Np——累计产油量,104 t;
Hcum——累计耗水量;
WORcum——累计水油比;
A1、B1、A2、B2——拟合系数,线性回归得到。
又由累计耗水量、累计水油比的定义,整理可得:
 (6)
(6)
式中:Qi——年注水量,104 m3;
Qw——年产水量,104 m3;
Qo——年产油量,104 t。
联立式(2)、式(6)可得:
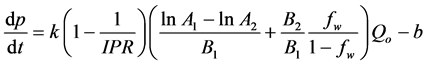 (7)
(7)
通过式(7)计算,可以确定出考虑无效注水的合理注采比。
3. 无效注水比例的确定方法
根据上面的推导,合理注采比的确定考虑了无效注水,反过来我们同样也可以通过推导,确定无效注水比例。
设某一阶段内无效注水比例为S,将S考虑进IPR中,将式(2)变换下形式,可以得到考虑无效注水比例的年压力恢复速度与注采比、年注水量的关系为:
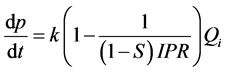 (8)
(8)
由于b同样为考虑无效注水等因素对压力恢复速度的影响,所以,联立式(2)和式(8),可以得到无效注水比例S的表达式为:
 (9)
(9)
4. 应用实例
通过对Z油田水驱实际动态数据拟合可得:
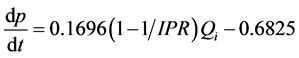 (10)
(10)
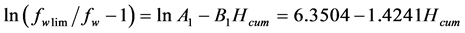 (11)
(11)
 (12)
(12)
可得:
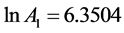 ,
,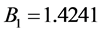 ,
,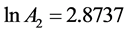 ,
,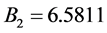
 (13)
(13)
将式(13)回代到式(10),整理可得到Z油田水驱注采比、含水率与压力恢复速度的关系为:
 (14)
(14)
Z油田2014年年产油量2.2606 × 104 t/a,含水率为0.465,得到注采比和压力恢复速度的关系曲线,如图1所示。
从1中可以看出,随着注采比的增大,压力恢复速度增加。2014年Z油田的地层压力为13.3 MPa,因此从图中不同的压力恢复速度可以计算出不同注采比条件下的地层压力,如表1所示。
按照油田开发纲要要求,地层压力应保持在原始地层压力附近。该油田原始地层压力为13.8 MPa,
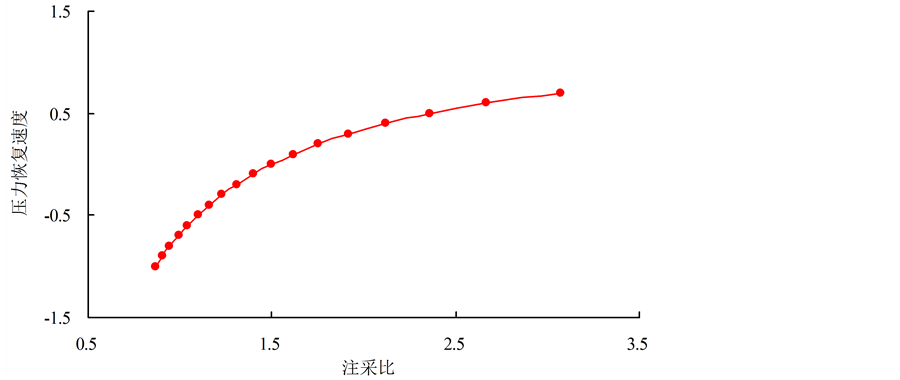
Figure 1. Injection-production ratio and pressure recovery speed curve of Z oilfield
图1. Z油田注采比与压力恢复速度的关系曲线

Table 1. Injection-production ratio and different formation pressure relational table of Z oilfield
表1. Z油田不同注采比与地层压力关系表
目前2014年地层压力为13.3 MPa,当Z油田的压力恢复速度为0时,即维持目前地层压力生产时,注采比为1.5,所以Z油田的合理注采比为1.5。
5. 油藏数值模拟方法验证
为了验证上述方法的正确性,我们应用油藏数值模拟方法对Z区块的合理注采比进行优选,并与上述方法优选的合理注采比进行对比。
通过地质建模软件Petrel建立Z油田的三维相控地质模型,然后通过油藏数值模拟软件Eclipse建立Z油田的数值模型,精细拟合之后,对Z油田的合理注采比进行了优选。但是此模型是建立在没有无效注水基础上的,所以优选注采比之前我们应考虑无效注水的影响。
通过式(9)计算Z油田各年的无效注水比例,得到无效注水比例平均为25%,由上述理论方法确定的合理注采比为1.5,所以,扣除无效注水,初步确定数值模拟中的合理的有效注采比为1.13。在1.13附近进行取值,通过数模模拟方法进行预测计算。对注采比分别取值0.95、1.05、1.15、1.25、1.35的五种方案预测10年,得到五种方案的采出程度曲线,如图2所示。
从图2中可以看出,当注采比小于1.15时,采出程度随着注采比的增大,增加幅度较大,当注采比大于1.15时,采出程度增加幅度变缓。因此优化Z油田的合理有效注采比为1.15。考虑无效注水比例25%后,油藏数值模拟方法最终确定Z油田的合理注采比为1.53,与通过推导的考虑无效注水的合理注采比理论方法计算的合理注采比1.5很接近,说明该理论方法是正确的,能很好的为其他油田合理注采比的确定提供理论依据,指导油田后续水驱开发。
6. 结论
(1) 通过物质平衡原理与Logistic旋回理论相结合的方法推导出了考虑无效注水的合理注采比的确定方法,同时推导出了确定无效注水比例的理论计算方法。
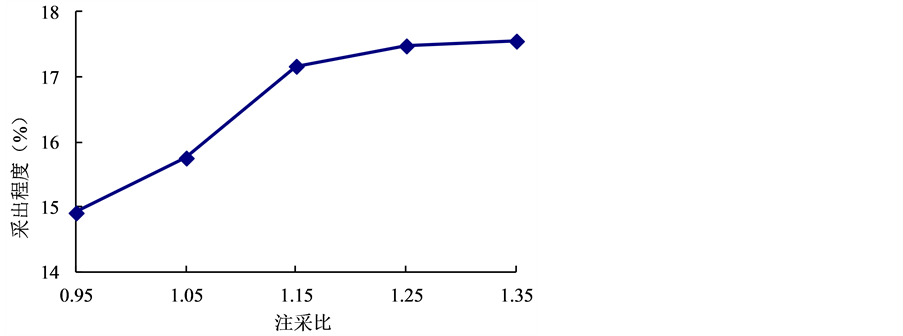
Figure 2. Z oilfield recovery degree curve of different injection-production ratio
图2. Z油田不同注采比的采出程度曲线
(2) 基于实际Z油田的生产数据,对该油田的合理注采比进行了计算,并与应用油藏数值模拟方法确定出的Z油田的合理注采比进行了对比,验证了此理论方法的正确性,对于水驱油田的开发具有一定的指导意义和实用价值。
参考文献(References)
[1] 屈斌学, 孙亚兰. 油田合理注采比的确定[J]. 吐哈油气, 2010, 12(4): 352-354.
[2] 杨国红, 尚建林, 王勇, 等. 油田注水配注合理注采比计算方法研究[J]. 成都理工大学学报(自然科学版), 2013, 40(1): 44-49.
[3] 徐晓燕. 榆树林油田合理注采比研究[D]: [硕士学位论文]. 大庆: 东北石油大学, 2011.
[4] 李程彤, 刘性全. 萨南开发区水驱高含水后期合理注采比的确定方法研究[J]. 大庆石油地质与开发, 2006, 25(4): 54-56.
[5] 王志军, 刘秀航, 董静, 等. 高含水后期油田区块注采适应性定量评价方法及调整对策[J]. 大庆石油地质与开发, 2005, 24(6): 51-53.
[6] 刘学峰, 赵玉欣, 唐磊, 等. 油田开发中后期合理注采比确定方法[J]. 河南石油, 2000, 14(2): 19-21.
[7] 王学忠. 无效注水量估算研究[J]. 断块油气田, 2007, 14(1): 67-69.
[8] 屈斌学. 油藏注采比计算方法综述[J]. 石油化工应用, 2009, 28(5): 7-10.
[9] 吴琼, 张文忠, 张春强. 应用逻辑斯蒂旋回模型预测注水量的方法研究[J]. 特种油气藏, 2011, 18(1): 67-69.