1. 引言
随着能源问题的日益加剧，分布式发电技术特别是风力发电技术正在快速的发展。而风电的波动性和随机性，给风电并网造成很大的困难。风电并网给电力系统带来的主要挑战有：风电并网引起的电网电压波动问题、电网谐波污染、低电压穿越问题、电力系统的频率稳定性问题等。要克服以上的困难，则需要对风电波动特性进行深入研究，进而对风电功率进行较为精确的预测。
对于风电功率波动特性，国内已有较多的研究，文献 [1] 对风电出力波动性进行了概述，说明了风电功率波动产生的机理及研究方向。文献 [2] 从相关性和平滑性两个方面，研究了不同时空尺度下，风电出力波动性的统计学规律，并用华北地区的实测数据对风电功率波动概率分布模型进行了检验。文献 [3] 做了基于概率统计的风电波动性研究，并对去波动化的对策进行了探讨。对于风电功率的预测，更是已从多方面用不同种方法进行了深入的研究。文献 [4] [5] 用数据挖掘结合其它智能算法对风电功率进行短期预测。文献 [6] 运用小波分析结合时间序列进行了短期预测算法的优化研究。就目前来说，多种智能算法结合的预测方法预测的精准性更加高。
依据《风电功率预测系统功能规范》 [7] ，无论是短期预测还是超短期预测，时间分辨率不小于15 min。在大多数预测中，也都是以分钟级的数据进行预测的，而风电功率的波动存在瞬变性，从秒级的数据到分钟级的数据明显存在波动信息的损失，且根据国际风能协会(International Wind Agency)所给出的风电并网后可能会对电力系统造成的影响 [8] ，从秒级到分钟级的风电功率波动信息对电力系统实时有功平衡和电压控制尤为重要 [9] ，但在这方面国内外研究甚少。本文以不同时间间隔作为标杆，讨论风电功率的波动信息损失，从数值特征上进行分析并给出描述。并对波动使用小波分析，比较不同时间间隔下不同波段的分布情况，进行功率损失程度的量化分析。以信息熵的大小作为衡量标准，描述风电功率信息波动情况。然后，对风电功率在不同时间间隔下进行预测，分析波动信息损失对预测的影响。本研究对风电功率预测的精度提高有一定的指导意义，对风电并网更加安全运行。
2. 不同时间尺度下风电功率波动的对比
以风电功率数值的差分描述风电功率的波动如下式：
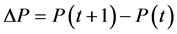(1)
其中，
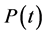为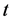
时风电场的输出功率，
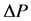为功率变化量，即功率的波动。
下面依据某风场的风电功率的5秒级数据，以某个时间间隔取一个点，得到5秒级、1分钟级、5分钟级、15分钟级四个时间间隔的数据，四个时间间隔的风电功率波动变化情况如下图1所示。
由以上的对比图可以看出，损失的信息主要为高频信息。同时，随着时间间隔的增大，风电功率波动的高频信息损失的越来越多，直至15分钟级数据，使波形产生了一定程度上的失真。那么，在不同时间间隔下到底损失了多少信息？怎样对损失信息进行描述？本文从以下三个方面进行讨论。
3. 波动幅值损失的分析
由以上分析，可知风电功率的幅值信息会由于时间间隔的增大有所损失，而损失的大多为高频信息。如表1所示，可以发现，随着时间间隔的增大，风电功率的方差越来越小，即表现在功率曲线上，波动程度越来越小。
本文通过功率波动之差来定义波动信息在幅值上的损失，如5 s到1 min的幅值损失如下式：
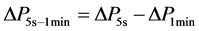(2)
其中，
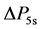与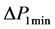
分别表示时间间隔5 s和1 min的功率波动值。
以某风电场的某一机组为例，5 s和1 min的波动情况如图2所示，5 s到1 min的幅值损失情况如图3所示。
由图2可知，在5 s到1 min的变化过程中差分波动的损失主要集中在−10~10的差分上，分布近似于t分布。
4. 基于小波变换的损失波段的研究
4.1. 小波变换
小波分析建立在调和分析、泛函分析和傅里叶分析的理论基础上，具有时频多分辨功能。它是用一个合适的母小波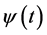
通过时间轴上的位移、放缩和幅度的变化产生一系列的派生小波，用系列小波对要分析的信号进行时间轴上的平移比较，获得用以表征信号与小波相似程度的小波系数。
4.2. 分析方法
首先，将差分后的功率曲线运用小波变换进行一维多尺度分解。分解原理是：首次分解将原始数据
Table 1. The variances of wind power in different time scale
表1. 各时间间隔下风电功率的方差
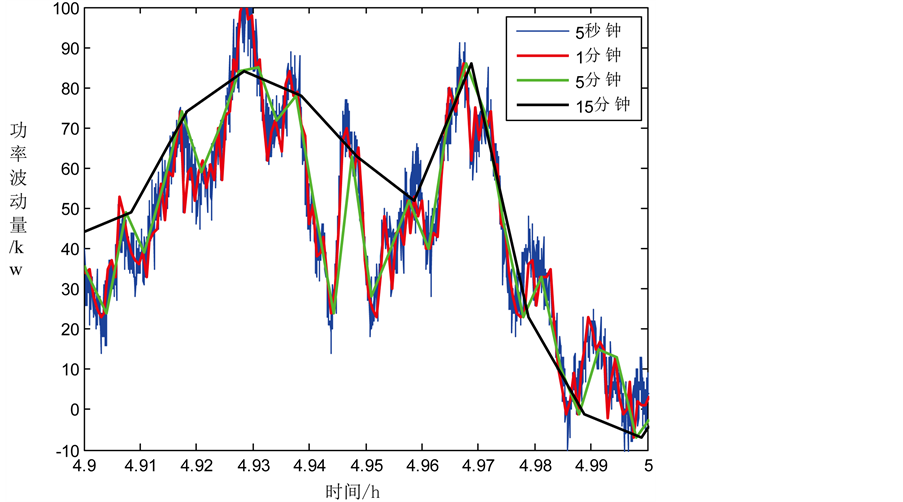
Figure 1. Fluctuation of wind power for four time interval of 5 s, 1 min, 5 min and 15 min
图1. 5 s、1 min、5 min、15 min四个时间间隔的风电功率波动
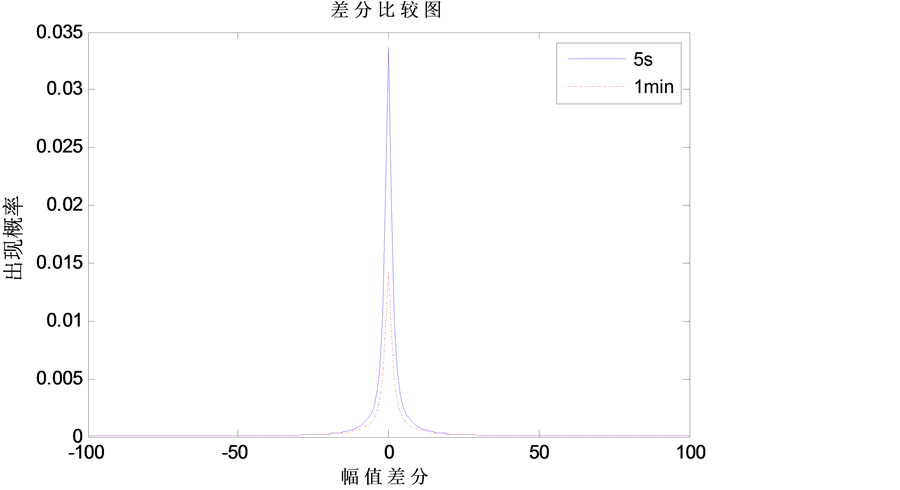
Figure 2. The fluctuation of the wind power of a wind turbine generator
图2. 某风电机组发出风电功率的波动情况
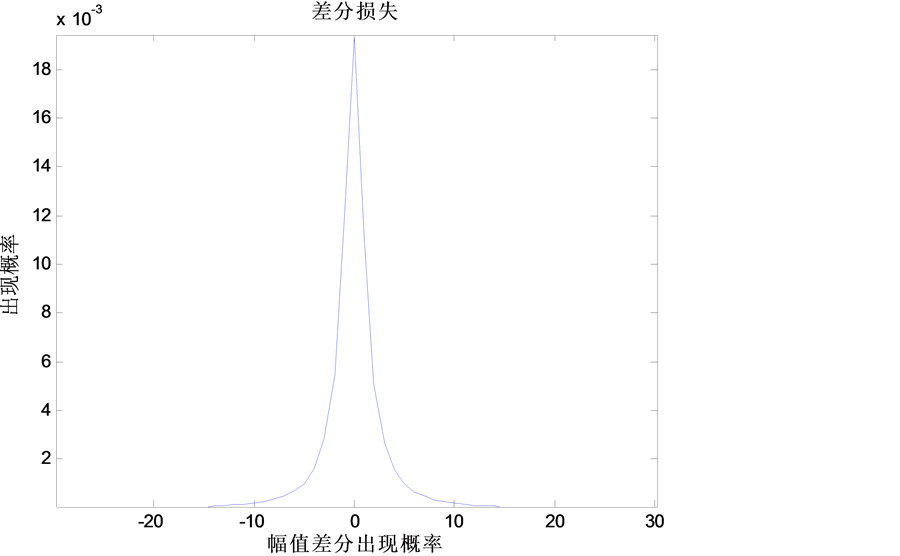
Figure 3. Amplitude loss of 5 s to 1 min
图3. 5 s到1 min的幅值损失情况
均分为高频分量和低频分量，再逐层均分高频分量，得到
次的高频分量和低频分量，每分解一次，得到相应的高频系数(细节系数)和低频系数(近似系数)。高频系数和低频系数可代表高频分量与低频分量的波形特征。然后，将每次分解的低频系数进行拟合，得到只含低频波的曲线。再运用插值，使各时间间隔的数据相等。接下来，对各时间间隔的低频或高频系数进行相关性分析，找出功率损失的波段，并说明该波段损失的重要性。
4.3. 实验结果
分解后的各频率波形如图4所示。
将5 s和1 min的低频系数曲线做相关性分析，用相关系数描述波形之间的联系。如图5，发现5台机组几乎都在分解次数为11时，低频系数不再强相关(强相关的相关系数临界值为0.8)，说明了1 min中的数据滤去了过多的高频分量，以至于此时两种时间间隔的波形有明显的差别。这样，一些幅值大的高频波或幅值突变的高频波不能被准确地描述出来。并且，对于每台机组，滤去的高频分量的频段几乎是一致的。换句话说，一台机组的过多高频分量被滤去，其它机组的高频分量同时被滤去，将会导致大规模的风电功率不准确，进而对电网的造成严重的冲击。
再从另一个角度，比较1 min和5 min波形的差异，利用5台机组的数据将1 min和5 min的高频系数做相关性分析，如表2所示，发现5台机组都是从分解次数为9开始，高频系数是强相关的。说明各机组功率波动的频率越高，相关性越强，表明了分解次数为9次以上的高频分量在风电波形描述中的重要性。
5. 基于小波变换的损失波段的研究
根据文献 [10] ，信息熵定义为离散随机事件的出现概率，从信息传播的角度，信息熵可以表示信息的
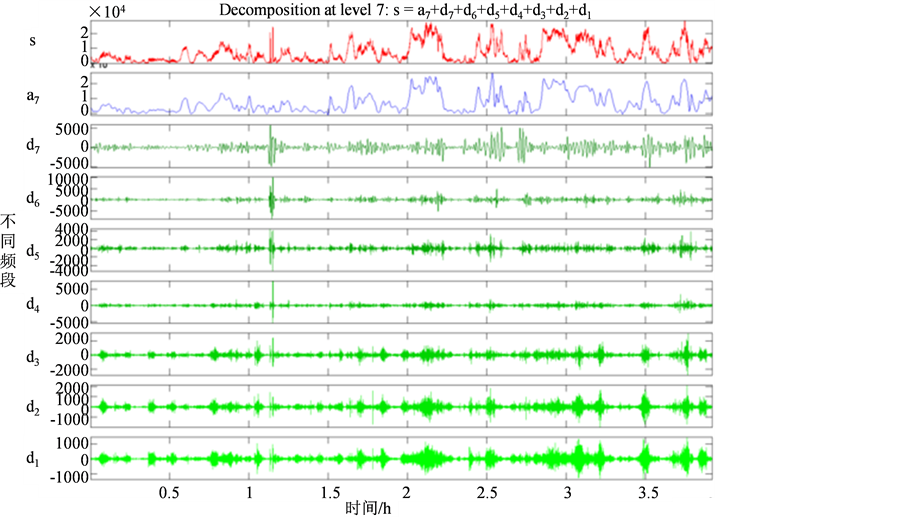
Figure 4. The curve of power after decomposing based on wavelet transform
图4. 小波分解后的功率曲线
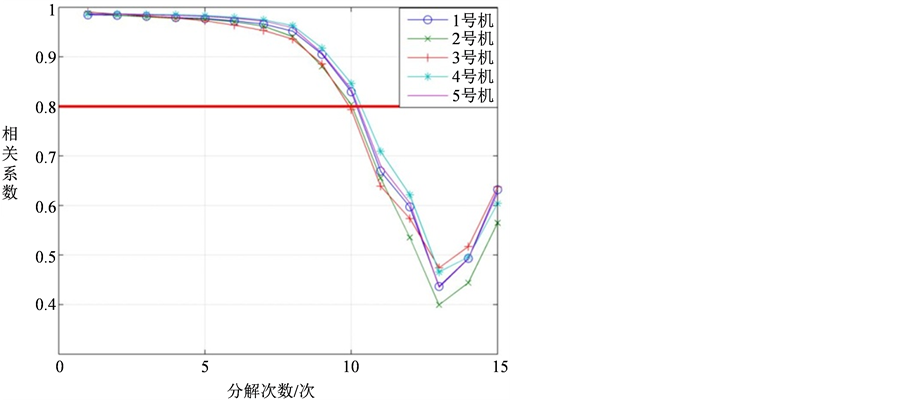
Figure 5. The interdependency of the coefficients of low frequency of 5 s and 1 min
图5. 5 s和1 min的低频系数的相关性
Table 2. The coefficients of high frequency
表2. 高频系数的相关性
混乱程度。而风电功率的波动具有随机性，信息熵恰恰能表现风电功率波动信息的波动性，体现波动信息的混乱程度，同时代表波动信息的价值。
在进行熵值计算前，需要对原始数据进行归一化处理：
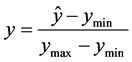(4)
再进行熵值计算：
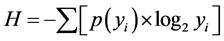(5)
其中，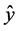
表示风电功率的原始值，
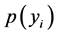表示功率为
时的概率，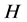
为对应数据组的信息熵值。
计算出20台机组在时间尺度为5 s、1 min、5 min、15 min的信息熵值，并对其取平均值，结果如图6所示。
1 min级，5 min级，15 min级的熵值分别为5 s级熵值的90.29%、83.91%、82.22%。可以看出，随着时间间隔的增大，信息熵越来越小，表明随机事件出现的概率变小，波动信息减小，信息的有序程度增加，波动信息的价值减小。
6. 不同时间间隔下风电功率预测精度分析
本文采用统计的方法，基于小波-BP神经网络预测模型，结合某风电场的5秒级输出功率的实测数据，对风电场的输出功率进行超短期预测。
6.1. 小波-BP神经网络预测模型的构建
风电功率具有一定的周期特性，如日特性、月特性、季节特性等。利用小波变换，可以将一个复杂的信号分解成不同频率段上的信号。小波神经网络是一种以BP神经网络为基础，结合小波分析和神经网络的优点，形成一种既能准确反映信号特征又具有自学能力前馈型神经网络 [11] 。小波神经网络主要有两种拓扑结构：一是将小波分析和神经网络融合，所谓融合就是指把小波基函数作为BP神经网络的隐含层函数。另一种是将小波分析与传统的神经网络组合，也就是将小波分析作为神经网络进行学习预测的数据处理工具，在对原始数据进行分解后，提取数据特征向量，为神经网络或机器学习做好准备 [12] 。本文采用第二种结构构建预测模型。
因此，首先运用小波变换将功率序列分解，并采用不同的神经网络对分解出的子序列进行训练和预测，然后将各个预测结果进行重构得到完整的预测结果 [13] ，流程如图7所示。
本文采用的小波神经网络算法步骤如下：
步骤1：对功率序列进行小波变换，变换成各频段的子序列。
步骤2：网络的初始化。随机初始化网络的连接权值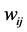
和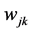
，设置网络学习速率
。
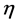步骤3：样本分类。把风电功率样本分为训练样本和测试样本，训练样本用于训练网络，测试样本用于测试网络预测精度。
步骤4：预测输出。把训练样本输入网络，计算网络预测输出并计算网络输出和期望输出的误差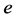
。
步骤5：权值修正。根据误差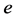
修正网络权值，使网络预测值逼近期望输出的误差
。
步骤6：判断算法是否结束，如果没有结束，返回步骤3 [14] 。
6.2. 预测结果的分析
建立如图7所示的小波-BP神经网络。首先将功率序列进行15次分解，并对分解出低频分量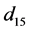
与
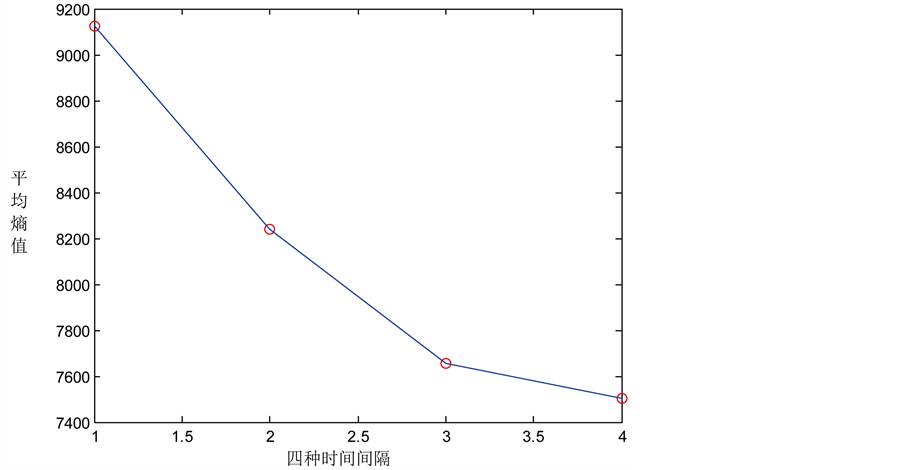
Figure 6. The average entropy of information of 20 assembling units for the time scale of 5 s, 1 min, 5 min and 15 min
图6. 20台机组在时间尺度为5 s、1 min、5 min、15 min的信息熵值的平均值
15个高频分量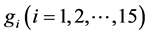
采用16个不同的BP神经网络进行预测，然后将16个网络的输出数据进行重构得到完整的输出功率。
使用某风电场2012年8月某单机输出功率的实测数据，进行时间间隔为5 min和15 min的风电功率预测。本文采用了3层神经网结构1-3-1，即第一层为输入层，输入节点有1个；第二层为隐含层，隐含神经元有5个；第三层为输出层，输出为1个。训练样本均为4700个，测试样本均为2100个，得到的预测结果如图8、图9所示。
然后，依据均方根误差(RMSE)和平均绝对误差(MAE)来判断预测的准确性 [7] ，计算公式如下：
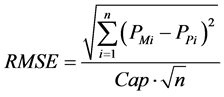(6)
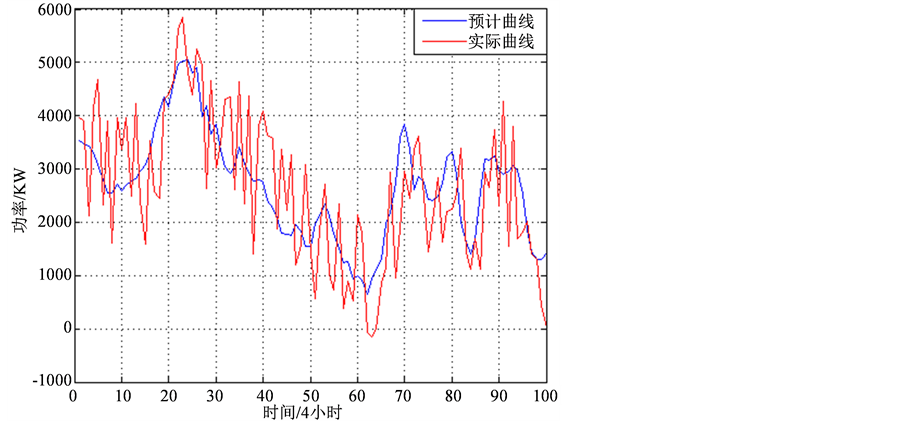
Figure 8. Predicted and measured wind power for the time scale of 5 min
图8. 时间间隔为5分钟的预测功率与实际功率
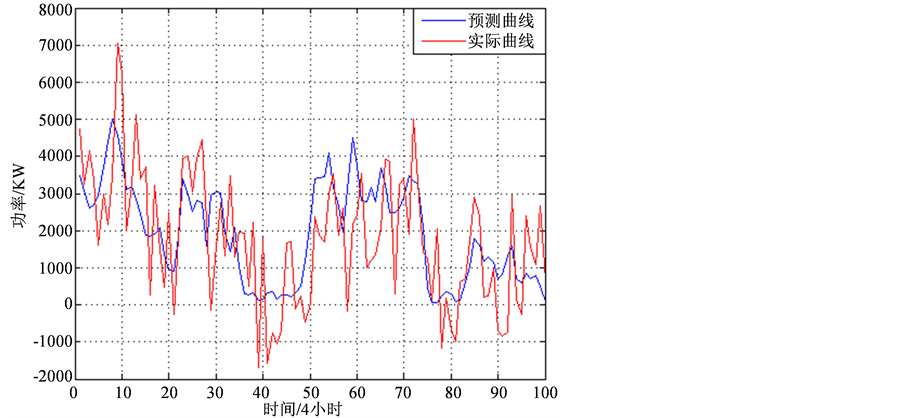
Figure 9. Predicted and measured wind power for the time scale of 15 min
图9. 时间间隔为15分钟的预测功率与实际功率
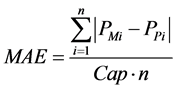(7)
其中，
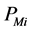是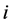
时刻的实际功率，
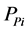是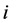
时刻的预测功率，
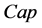为平均开机容量，
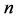为样本个数。
对于时间间隔为5 min的预测，均方根误差为15.6%，平均绝对误差为19.55%。对于时间间隔为15 min的预测，均方根误差为17.8%，平均绝对误差为24.75%。
由不同时间间隔的功率预测误差可以看出，时间间隔越大，预测误差越大。表明在增大时间间隔的过程中，失去了功率波动规律性的部分分量，不利于功率的预测。
7. 风电波动信息损失的影响
如果无法对风电输出功率做精确的预测，导致波动信息的损失，会对电网的电能质量和有功功率平衡造成影响。根据以上三方面对风电波动信息损失的分析，结合风电波动对电网的影响 [6] [15] ，得出以下几点不同时间尺度下风电波动信息损失的影响。
7.1. 对电网电压的影响
风电的接入，由于风电机组对无功功率的消耗，会使接入点附近局部地区的母线电压降低。而接入点电压的变化很大程度上取决于注入功率的变化。功率变化波动信息的损失，会使接入点电压波动超过安全范围时而无法被预测到，进而会影响配电网其他用户的供电电压，甚至会导致区域电压崩溃。
7.2. 对电网频率的影响
频率作为电能质量的重要指标，中国电能质量标准规定，正常情况下频率偏差不应超过±0.2 Hz。如果风电波动没有被准确地预测，电网中的有功功率会不平衡，从而造成频率的偏差，即使是很小的偏差，也会造成用电设备出力降低、设备工作异常，甚至发电机组跳脱、系统频率崩溃等严重事故 [16] 。
对于风电并网，一般要求风电场连续运行和起停过程必须具有控制有功功率的能力，一方面控制功率变化率，另一方面根据电网需要限制风电场输出功率 [17] 。如果时间间隔过大，会无法准确地控制功率的大小和变化率。
7.3. 对经济的影响
风电接入后，电网必然面临需要增加备用容量以保证电网运行风险水平的局面。如果风电预测精度不够，则需要使用更多的备用容量，造成了经济的损失。并且，风电预测误差的增加，会使风电预期值难以在调度过程中直接使用，甚至会导致调度过程中的误判断，如不合适的弃风，使风电价值降低，大大降低风电引入的经济性。风电功率波动造成的电压质量的下降，使对设备的损耗增加，以及不安全事故的发生造成巨大的经济损失。
8. 总结
本研究基于风场的实测数据，采用三种分析方法，研究了不同时间尺度下风电功率波动信息的损失及其影响，得出了如下结论：
1) 所取的时间间隔越大，风电波动信息损失得越多,表现在功率曲线上是波动越来越小；风电波动信息损失为高频分量，且不同时间间隔的损失之间是相互独立的。
2) 基于小波分析的低频系数相关性分析结果暗示，对于几乎每一台机组，损失的高频分量的频段是一致的；高频系数相关性分析的结果表明，高频分量在波动分析中很重要，但时间间隔的增大，会导致功率曲线中高频分量的缺失。
3) 基于信息熵的分析表明，随时间间隔的增大，信息的混乱程度较小，价值也减小；在进行风电功率预测时，所选取预测数据的时间间隔越大，预测的误差越大。