1. 引言
资本资产定价模型(CAPM)是由William Sharpe和John Lintner等人1964年在资产组合理论的基础上发展起来的,是第一个关于金融资产定价的均衡模型和可以进行计量检验的金融资产定价模型 [1] 。由于股票等资产资产未来收益的不确定,资本资产定价模型本质是讨论资本风险与收益的关系。自20世纪80年代以来许多金融异象的挑战下,对风险厌恶型投资者,资产定价模型默认风险和收益之间存在正相关关系,但来自金融异象的实证结果则并非如此。理论上,风险和收益在资本资产定价模型中起着重要的作用,在投资者厌恶风险的假设下,资产定价模型隐含着风险和收益正相关的内涵。在Sharpe-Lintner-Mossin的股票交易均值–方差均衡框架下,持有某一资产的预期超额收益和该资产收益与市场组合之间的协方差成正比。在Merton (1973)提出的跨期资本资产定价模型(ICAPM)中,股票市场的条件预期超额收益和条件方差呈正相关关系。风险与收益之间的这种均衡关系是金融经济学的基础,甚至被称作“金融学第一基本原理”(Ghysels等,2005)。
在中国这个典型的新兴证券市场中,具有诸多不同于西方发达证券市场的特征。在此背景下许多学者对中国证券市场风险与收益间的关系进行了研究,然而他们所采用的实证方法基本上属于CAPM的范畴 [2] ,实证结果却相互矛盾。而且,无法用标准金融理论给出合理的解释,因此,有必要进行更深入的研究。
2. 资本资产定价模型CAPM
资本资产定价模型综合了证券组合理论和资本市场理论,以证券组合投资理论为基础,因此有关与证券组合投资的假设都适用于资本资产定价模型;同时资本资产定价模型另一方面又来自资本市场,所以对资本市场也需要提出一些假设。其主要假设有:第一,投资者能在预期收益率和标准差或方差的基础上选择证券组合;第二,针对一个时期内,所有投资者的预期都是一样的;第三,资本市场上没有摩擦 [3] 。
资本资产定价模型有两种本质相同的形式。第一,Sharpe-Lintner模型假设投资者能以无风险收益率贷款,被认为是标准的CAPM,是我们最为熟知的表达形式 [4] :
 (1)
(1)
其中,

其中: 表示证券
表示证券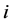 的期望收益率;
的期望收益率; 表示无风险资产收益率;
表示无风险资产收益率; 表示证券
表示证券 的
的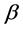 系数,即系统风险系数;
系数,即系统风险系数;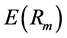 表示市场投资组合期望收益率。第二,Black在无风险借贷的假设下,提出更为普遍的CAPM形式,即:
表示市场投资组合期望收益率。第二,Black在无风险借贷的假设下,提出更为普遍的CAPM形式,即:
 (2)
(2)
其中,将(1)式中的无风险资产收益率 换成了市场组合中的零
换成了市场组合中的零 的资产收益率
的资产收益率 [5] 。但对CAPM检验一般是针对Sharpe-Lintner形式进行,公式(1)表示为当资本市场达到均衡时,每项资产i的收益都和它与市场组合的协方差呈线性关系。若一项资产与市场组合m的收益的协方差为零(
[5] 。但对CAPM检验一般是针对Sharpe-Lintner形式进行,公式(1)表示为当资本市场达到均衡时,每项资产i的收益都和它与市场组合的协方差呈线性关系。若一项资产与市场组合m的收益的协方差为零( ),该项资产的收益则为
),该项资产的收益则为 。因此,在CAPM中是资产收益与市场组合收益的协方差,不是该资产方差,决定着该资产的期望收益。
。因此,在CAPM中是资产收益与市场组合收益的协方差,不是该资产方差,决定着该资产的期望收益。
CAPM是一个事前线性模型,本文对其进行检验时即将理论的资本资产定价模型转换为可以利用历史数据的事后形式,其一般模型为:
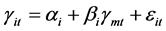 (3)
(3)
其中,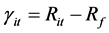 为股票
为股票 的超额收益率,
的超额收益率, 为市场超额收益率;
为市场超额收益率;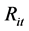 为股票
为股票 第
第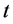 期的收益率,
期的收益率, 为市场组合第
为市场组合第 期的收益率,
期的收益率, 为随机误差。方程(3)通常为确定系数
为随机误差。方程(3)通常为确定系数 的“一次回归”方程。
的“一次回归”方程。
确定系数 后,就可以用其进行单个股票或组合收益与
后,就可以用其进行单个股票或组合收益与 相应的检验。其回归方程为:
相应的检验。其回归方程为:
 (4)
(4)
通常将方程(4)称为“二次回归”方程。
3. 数据选取与分析
本文采用2010年1月8日到2014年12月31之间沪深300市场中股票的周收益率,除去一些数据不全的股票,剩下125组股票,每支股票152个数据作为研究对象。数据来源于大智慧。分析软件为R软件。
对该125支股票收益率和沪深300指数的市场收益率的时序图进行分析,可以看出其皆为平稳,其中只列出11支股票的市场收益率和沪深300指数市场收益率时序图,如图1所示。
此外再对该126组数据进行单位根检验(DF),其检验结果如表1所示。
从表一可以看出,该126组数据的都为p < 0.05,则该数据都是一阶平稳的,因此可以用于数据分析。
无风险利率的确定,国外研究中常用一年期的国债利率或银行同业拆借利率来代替无风险利率。但我国现今国债以长期品种为多,且国债回购交易大多是机构投资者,因此用国债利率代替无风险利率代表性不够。在中国股票市场上,相当部分是个人投资者,且投资机会主要为:储蓄、股票和国债,其中储蓄比例更大。所以本文采用三个月期定期存款利率代表无风险利率,并将其转换成周利率。
4. 模型与实证
本文对标准CAPM模型在沪深300市场中的检验,计算步骤如下:
第一:将时间分为三个时段,2011年1月-2012年1月为一期;2012年1月-2013年1月为二期;2013年1月—2014年1为三期。
第二:用一期的数据对每支股票的周超额收益率和市场周超额收益率进行回归,其基本模型为公式(3):

估计出每支股票的系数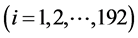
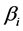 ,并根据
,并根据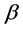 系数由小到大的顺序构造19个股票组合(每组10支股票,最后一组12支除外)。在后面的分析中,将用这19组数据的组内平均值构造时间序列,以减少因单只股票分别估计所带来的误差。
系数由小到大的顺序构造19个股票组合(每组10支股票,最后一组12支除外)。在后面的分析中,将用这19组数据的组内平均值构造时间序列,以减少因单只股票分别估计所带来的误差。
第三:用二期的数据对已有组合的周超额收益率与市场的周超额收益率进行回归,估计出每个组合的系数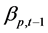 和回归残差的标准差
和回归残差的标准差 (作为影响股票组合
(作为影响股票组合 的超额收益率与
的超额收益率与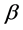 无关的因素 [6] [7] 。
无关的因素 [6] [7] 。
第四:用第三期和上面得到的各数据,对以下的模型进行回归分析:
图1. 市场和每支股票的周超额收益率y、xi的一阶差分时序图

Table 1. The return of CSI 300 market and stocks unit root test
表1. 沪深300中市场和每支股票收益率单位根检验结果
 (5)
(5)
 (6)
(6)
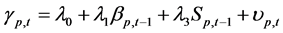 (7)
(7)
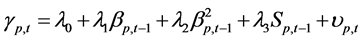 (8)
(8)
其中, 为
为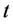 期的组合超额收益率,
期的组合超额收益率,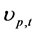 为残差项,
为残差项, 。
。
回归结果如下。
模型一:

模型二:

模型三:

模型四:
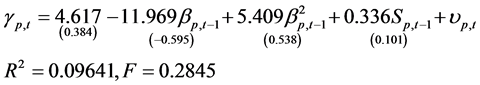
其中,括号里面的值为 值。
值。
从上述四个模型可以看出, 和
和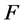 值都比较小。且在5%显著性水平下,模型的各参数也都没有通过显著性检验。所以上述的四个模型都不适合于本文的样本数据。问题的根源很可能在于模型中所使用的股票及股票组合的
值都比较小。且在5%显著性水平下,模型的各参数也都没有通过显著性检验。所以上述的四个模型都不适合于本文的样本数据。问题的根源很可能在于模型中所使用的股票及股票组合的 系数的不稳定 [6] [7] 。为此将三个时期各组合的
系数的不稳定 [6] [7] 。为此将三个时期各组合的 系数、三个时期平均
系数、三个时期平均 系数,以及第三期的平均周超额收益率整理于表2。
系数,以及第三期的平均周超额收益率整理于表2。
从表2可以看出,由于第一期的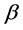 系数是进行分析时所按照从小到大排序的,但第二期、第三期,以及三期平均
系数是进行分析时所按照从小到大排序的,但第二期、第三期,以及三期平均 系数都呈现杂乱无章的顺序,不再存在从小到大的顺序。从而,股票组合的
系数都呈现杂乱无章的顺序,不再存在从小到大的顺序。从而,股票组合的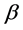 系数是不稳定的。且第三期的平均周超额收益率也不存在由小到大的顺序。因此,下面直接对各期收益率的截面数据来估计股票的
系数是不稳定的。且第三期的平均周超额收益率也不存在由小到大的顺序。因此,下面直接对各期收益率的截面数据来估计股票的 系数,并将所得
系数,并将所得 值与当期的超额收益率相对应以检验CAPM。由于各期所得结果都大致相同,下面只列出用第三期进行分析的结果。
值与当期的超额收益率相对应以检验CAPM。由于各期所得结果都大致相同,下面只列出用第三期进行分析的结果。
模型五:
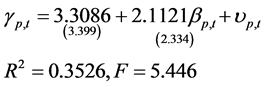
模型六:


Table 2. The coefficient β of every portfolio and average excess return of the thirdly period
表2. 各组合的β系数与第三期平均超额收益率
模型七:

模型八:

从上述模型五至八可以看出:
(1) 在5%显著性水平下,各模型的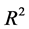 和
和 值都比较小,即模型中股票超额收益与各解释变量之间的线性关系在总体上不显著。
值都比较小,即模型中股票超额收益与各解释变量之间的线性关系在总体上不显著。
(2) 模型五,当用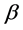 作为解释变量时,在5%显著性水平下其系数是显著的,而股票收益率与
作为解释变量时,在5%显著性水平下其系数是显著的,而股票收益率与 之间呈正相关关系。
之间呈正相关关系。
(3) 模型六至八,当用 、
、 和回归残差的标准差作为解释变量时,各模型的
和回归残差的标准差作为解释变量时,各模型的 值变化也不是很明显,且各系数也不显著。
值变化也不是很明显,且各系数也不显著。
以上各数据显示,各模型的拟合优度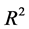 都比较小,所以不能认为沪深300股的波动率与收益率之间存在明显的线性相关关系。这也与资本资产定价理论里面高风险与高收益呈正相关关系相互矛盾,但是由于中国的股市是一个新兴的市场,股市的变动不仅和投资者存在很大的关系,还和投机者有关。因此这也说明沪深股市中股民还是以投机性为主 [8] [9] 。
都比较小,所以不能认为沪深300股的波动率与收益率之间存在明显的线性相关关系。这也与资本资产定价理论里面高风险与高收益呈正相关关系相互矛盾,但是由于中国的股市是一个新兴的市场,股市的变动不仅和投资者存在很大的关系,还和投机者有关。因此这也说明沪深股市中股民还是以投机性为主 [8] [9] 。
5. 研究结论
本文用CAPM对沪深300指数中股票波动率和收益率之间的关系进行分析,结果显示收益率与波动率之间正相关关系不明显。虽然这与利用标准金融模型的实证结果不同,但却与沪深市场情景吻合。由于中国股市的不完整性和投机性的存在,所以使得高风险与高收益不完全对称是可以解释的。因此,中国股市这个新兴的金融行业而言,还有许多值得完善和提高的地方,同时中国股市也是一个值得投资的地方。