1. 引言
信息时代的飞速发展让信息传递更加迅速和便捷,数字图像信息因其具有形象直观传递信息的特点,在日常的数据通信中运用得尤为广泛。因此,数字图像在传递过程中的安全问题也更加值得我们关注。
由于数字图像数据量庞大,冗余性严重,且数据存储结构呈二维空间分布,用传统的加密方式加密效率非常低,需要一种适合数字图像的新的加密方式来提高加密效率 [1] 。混沌映射与加密系统两者之间的诸多共性,例如:混沌的拓扑传递与混迭特性类似于密码的扩散与混淆特性;混沌对参数的敏感性则对应着密码对密钥的敏感性;混沌映射通过多轮的迭代获得指数分离的轨道,加密系统则通过多轮的置乱与替换将明文打乱 [2] 。基于混沌映射的图像加密算法受到了许多学者的青睐 [3] 。本文在前人研究基础上,探讨基于Logistic混沌映射的比特级数字图像加密方法的可行性,设计了图像的比特级置乱步骤。
2. Logistic映射
Logistic映射是一种应用十分广泛的动力系统,其一般定义形式如下 [4] :
 (1)
(1)
图1为Logistic映射的分岔图。其中,分岔系数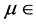 (0,4),状态
(0,4),状态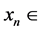 (0,1)。由图示可知当
(0,1)。由图示可知当 (3.5699456,4]时,Logistic映射的输入输出都分布在(0,1)上,Logistic映射工作于混沌状态。
(3.5699456,4]时,Logistic映射的输入输出都分布在(0,1)上,Logistic映射工作于混沌状态。
3. 加密解密算法
一般的加密过程分为两个模块,一部分是像素融合模块,一部分是像素置乱模块。两模块之间相互独立,均可单独对图像进行有效的加密操作。为了提高加密的安全性,通常将两种加密方式结合起来使用 [5] 。本文采取的是比特级的加密方式,这种加密方式可以只进行一步置乱操作,但在效果上却可以达到像素融合的目的。下面是具体算法:
第一步,先将原始图像的像素值二维矩阵由L行R列转换成L × R行一列的形式,每一行有一个十进制数,表示一个像素值。
第二步,既然要做比特级的操作,我们就要把原始图片的每一位像素值由十进制化成二进制形式,像素值在区间(0,255)上,所以每个十进制像素值由八位二进制数表示,不足八位的高位由0补齐。具体换算公式为:
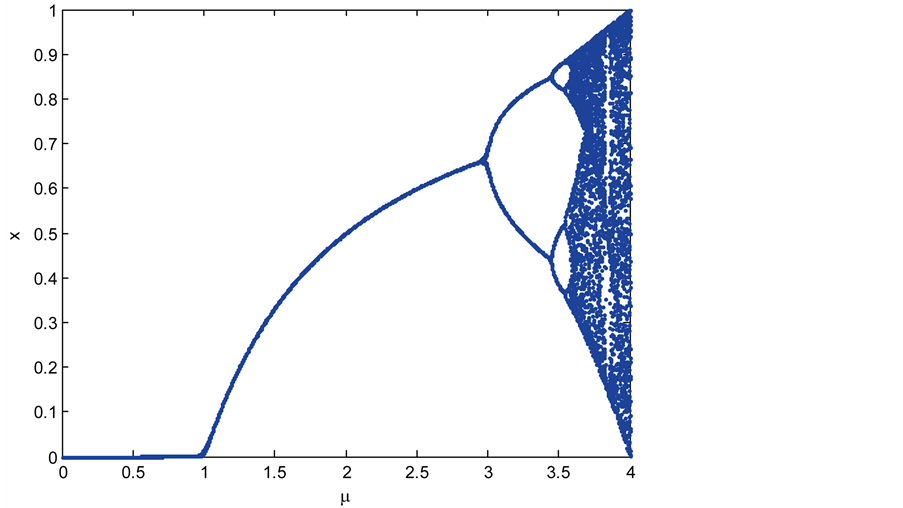
Figure 1. The bifurcation diagram of Logistic mapping
图1. Logistic映射的分岔图
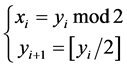 (2)
(2)
其中 ,
, 表示二进制数的第i位(第一位为最低位),
表示二进制数的第i位(第一位为最低位),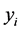 是原始像素值,
是原始像素值,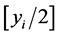 表示除以2再取整。
表示除以2再取整。
我们把每一位二进制数看成是一个数,换算过后由十进制数表示的L × R行一列的矩阵就变成了L × R行八列的形式。
第三步,将L × R行八列的矩阵继续整形成L × R × 8行一列的形式。
第四步,利用式(1)及初始值生成混沌序列,即迭代Logistic映射直到产生L × R × 8个完全不同的值为止,记作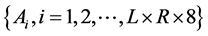 ,其中L × R是需要加密的图像的大小。
,其中L × R是需要加密的图像的大小。
第五步,对混沌序列 进行排序,得到位置索引,根据位置索引对上述L × R × 8行一列形式的矩阵进行置乱。
进行排序,得到位置索引,根据位置索引对上述L × R × 8行一列形式的矩阵进行置乱。
第六步,对置乱后的L × R × 8行一列形式的矩阵做第一步到第三步的逆操作。即先由L × R × 8行一列形式整形成L × R行八列的形式;再把L × R行八列矩阵每一行的八个数看成是二进制的每一位合并成一个二进制数,将这个二进制数换算成一个十进制数,L × R行八列的矩阵变成L × R行一列;最后将L × R行一列的矩阵还原成L行R列的形式成为加密图像。
解密过程是加密过程的逆运算。
4. 加密解密数值实验
如下图2所示,对原图像(a)用密钥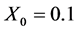 ,
,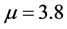 进行加密,得到加密图像(b)。再分别用密钥
进行加密,得到加密图像(b)。再分别用密钥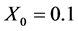 ,
,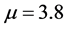 、密钥
、密钥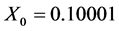 ,
,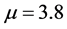 和密钥
和密钥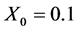 ,
, 对加密图像进行解密,得到解密图像(c1) (c2) (c3),由三个解密图像可以看出,只有当使用正确的密钥解密时才能恢复出原图像,否则会得到杂乱无章的图像。
对加密图像进行解密,得到解密图像(c1) (c2) (c3),由三个解密图像可以看出,只有当使用正确的密钥解密时才能恢复出原图像,否则会得到杂乱无章的图像。
5. 实验结果及安全性分析
5.1. 密钥空间和雪崩效应分析
5.1.1. 密钥空间分析
密钥主要是由Logistic映射的控制参数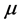 和初始值
和初始值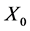 组成 [6] 。由Logistic映射的特点可知,
组成 [6] 。由Logistic映射的特点可知,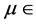 [3.5699456,4],
[3.5699456,4], (0,1),所以密钥
(0,1),所以密钥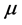 可以取区间[3.5699456,4]上的任意浮点数,而密钥
可以取区间[3.5699456,4]上的任意浮点数,而密钥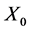 则可以取区间(0,1)上的任意浮点数,可见密钥空间相当大。
则可以取区间(0,1)上的任意浮点数,可见密钥空间相当大。
5.1.2. 密钥雪崩效应分析
从密钥更换的有效性考虑,一个秘密算法对密钥的变化应该是敏感的,即密钥具有所谓的雪崩现象。我们分别改变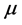 和
和 的值,观察加密图像,考察算法对密钥的敏感度。
的值,观察加密图像,考察算法对密钥的敏感度。
图3和图4示当参数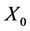 ,
,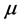 分别改变0.00001的情况下,不能从密文中提取更多的信息,这表明算法对密钥非常敏感。
分别改变0.00001的情况下,不能从密文中提取更多的信息,这表明算法对密钥非常敏感。
5.2. 抗统计攻击
5.2.1. 直方图分析
图5给出了原始图像和加密图像的灰度值统计直方图,由比较可知,变化前后的直方图有明显的变化,原图像的统计直方图分布不均匀,而加密后的统计直方图呈均匀分布,一定程度上掩盖了变换前原图的分布规律。而传统的置乱加密算法只改变像素点的位置,不改变直方图的分布。
图3. 密文对密钥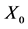 的敏感度
的敏感度
图4. 密文对密钥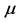 的敏感度
的敏感度
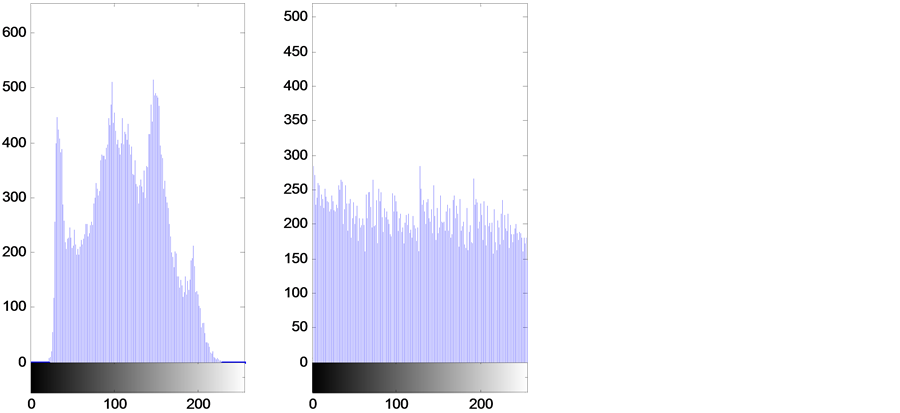
Figure 5. The gray value histogram of the images encrypted before and after
图5. 加密前后图像灰度值直方图
5.2.2. 相关性分析
在测试图像中,随机选取1000对相邻(包括水平、垂直和对角方向相邻)的像素点对,记为( ),其中
),其中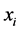 ,
,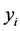 分别代表第 对像素的两个像素值。按如下定义的相关系数,计算这1000对像素灰度值之间的线性相关系数。
分别代表第 对像素的两个像素值。按如下定义的相关系数,计算这1000对像素灰度值之间的线性相关系数。
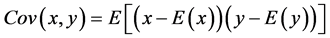 (3)
(3)
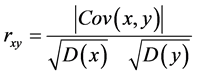 (4)
(4)
式中,x,y表示两个相邻的像素灰度值。在实际测试中用如下离散化的计算公式 [7] [8] :
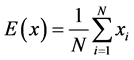 (5)
(5)
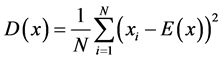 (6)
(6)
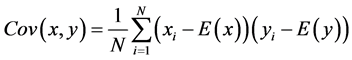 (7)
(7)
以相邻两像素灰度值为x,y坐标,得到加密前后相邻两点的相关性分析结果如图6所示。
表1列出了对明文图像和密文图像多次随机选取1000对像素测试后得到的相关系数。可以看出,加密前的图像像素之间具有较强的相关性,经过加密过后,这种相关性已经基本被破坏了。
6. 结束语
本文提出了一种基于混沌序列进行比特级图像加密的算法,将图像的每一位像素值做二进制转化,形成一维的0和1的数码串。对二进制数码串进行混沌置乱操作,可同时达到像素融合的目的,实现图像加密。根据数值实验结果可以看出,基于Logistic混沌映射的比特级数字图像加密算法的加密效果较好,能很好的去除图像的相关性,用错误的密钥不能解密出原始图像。从安全性分析结果可以看出,密

Figure 6. The correlation analysis between adjacent pixels of plaintext and ciphertext
图6. 明文图像和密文图像相邻两点的相关性分析结果

Table 1. The correlation coefficient between adjacent pixels of plaintext and ciphertext
表1. 明文图像和密文图像相邻像素间的相关系数
钥的雪崩效应明显,不同的密钥生产的加密图像差别较大。算法有较强的抗统计攻击能力,能满足安全保密的数据传递。