1. 引言
准确评估通信指挥效能是提升通信装备作战能力的关键一环，然而，由于通信指挥指标体系的客观复杂性，其部分指标的量化存在很大困难，有些指标只能依靠专家主观评判，很难得到定量值，层次分析法为这类效能评估问题提供了一条有效的求解途径。层次分析法将评估指标体系划分为目标层、准则层和方案层，在此基础上汇集专家意见将各因素形成判断矩阵，进行定量和定性分析，给出量化评估结果。在基于层次分析法的效能评估过程中，如何在最大程度地尊重专家意见、保留原始数据的基础上，对不一致的判断矩阵进行一致性调整，是影响评估效果和评估质量的一个关键步骤。针对基于层次分析法的效能评估过程中这一问题，本文提出了一种两阶段一致性调整方法。
2. 相关工作
通信指挥效能评估包括对指挥控制能力、通信保障能力、指挥活动质量等众多因素的综合评估 [1] ，各因素相互影响且又缺少定量数据支持，层次分析法是解决这一问题的有效方法。层次分析法(Analytic Hierarchy Process, AHP) [2] 是一种定性与定量分析相结合的多目标决策分析方法，在效能评估 [3] 、风险评价 [4] 等领域有广泛的应用。层次分析法的基础是构造判断矩阵，即通过决策专家对评判指标进行两两比较，并用标度的形式对比较结果进行量化表示。然而，对于复杂问题，根据专家评判得到的判断矩阵很难保证完全一致，因此对判断矩阵进行一致性检验和调整，是评估决策的关键。
判断矩阵的一致性检验存在如何保持一致性和合理性 [5] [6] 的问题。一致性调整方法已有不少改进策略 [7] - [9] ，包括广义最小二乘法 [10] 、三标度构造法 [11] 等。其中一类策略是构造一致性判断矩阵，比较原判断矩阵和一致性判断矩阵，反复修改。文献 [12] [13] 分别描述了直接构造一致性判断矩阵的方法。文献 [13] 提出反复调节原判断矩阵和导出的完全一致性判断矩阵间调节系数，构造调节矩阵，能够满足一致性要求，但计算量大，对专家意见改动多。文献 [14] [15] 提出一种构造一致性矩阵简化方法，分为四个阶段，每个阶段检测每个比较的一致性。文献 [16] 提出在遵守次序一致性的基础上调节矩阵元素。这些改进方法各有优势，但对通信指挥效能评估不够简洁、完善。
本文使用层次分析法评估通信指挥效能，首先针对现有判断矩阵一致性检验方法的缺陷，提出一致性调整的两阶段方法，使得判断矩阵尽量保留专家原始意见、满足一致性并减少计算量。然后建立评估通信指挥效能的指标体系，使用一致性的两阶段调整方法导出一致性判断矩阵，合理分配各要素权重，为准确评估通信指挥效能提供科学依据。
3. 基于层次分析法的通信指挥效能评估方法
3.1. 问题求解框架
基于层次分析方法求解通信指挥效能评估问题的总体思路是利用分层结构评估针对通信指挥效能的多种备选方案的优劣。首先建立层次结构模型，目标层是评估通信指挥效能，准则层是专家给出的多种指标，方案层是各种备选方案。其次对准则层指标构建判断矩阵，对判断矩阵进行一致性检查和调整，计算层次单排序和总排序的权重。最后根据计算的各种备选方案对目标的权重大小，选择合适的方案。
3.2. 判断矩阵的一致性调整方法
基于层次分析法进行通信指挥效能评估，对判断矩阵的一致性检验和调整是关键。在对判断矩阵进行一致性调整时，以最大程度地保留专家原始意见且简化计算为目标，本文提出了判断矩阵的两阶段一致性调整方法。第一阶段对专家给出的判断矩阵A进行一致性检查，从判断矩阵A中导出完全一致性矩阵
，计算偏差比例，发现两个矩阵间的偏差最大的元素aij。第二阶段采用次序一致性 [16] 等规则调整偏差最大的元素，构造修正矩阵A'，既达到满意的一致性又最大程度保留专家意见。
3.2.1. 构造完全一致性矩阵并发现不符合一致性的元素
设专家决策得出的原判断矩阵为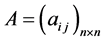
，根据AHP原理知A是一个正互反矩阵。根据文献 [15] 所提的原判断矩阵一致性逼近原理导出矩阵A的完全一致性判断矩阵
。
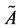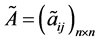，元素
。
计算两个矩阵元素的偏差比例
，形成矩阵B。通过偏差bij发现矩阵A中不符合一致性的元素。计算偏差距离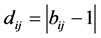
形成矩阵D，根据dij的大小定位偏差距离最大的元素aij。
3.2.2. 构造修正矩阵
根据第一阶段获得的完全一致性矩阵
和偏差较大的元素aij，根据一定规则构造修正矩阵A'。
规则1：调整方向原则。矩阵A中元素值调整参照偏差比例bij，若bij < 1则矩阵A中的元素aij需要放大；若bij > 1则矩阵A中的元素aij需要缩小；若bij = 1，不需要调整。
规则2：发现偏差最大元素原则。计算元素偏差距离dij，根据Max(dij)的值发现矩阵A中偏差最大的元素，修改偏差距离数值最大的dij所对应的元素aij的值。如果对应元素aij = 9且bij < 1，不调整aij的值；如果aij = 1/9且bij > 1，也不调整aij的值。此时根据Max(dij)的值选择偏差第二大的元素，修改对应的元素aij的值。
规则3：调整间距原则。每次调整元素aij的间距为1~9标度离散区间的一个相邻离散取值，即在[1/9, 1/8, 1/7, 1/6, 1/5, 1/4, 1/3, 1/2, 1, 2, 3, 4, 5, 6, 7, 8, 9]中，调整增大或减小一个相邻取值。如果bij < 1且aij < 9，调整aij的值增大一个相邻取值，如原来aij = 1/4，则调整后为1/3；如果bij > 1且aij > 1/9，则调整aij的值减小一个相邻取值，例如原来aij = 7，则调整后为6。
第二阶段在构造修正矩阵A'过程中，根据规则依次修改偏差最大的元素值，每一次修改后需要进行一致性检验，保证调整后修正矩阵的一致性在允许的范围内，一致性算法步骤如算法1。
下面举例说明所提方法能够自动构造出既满足一致性又符合专家原始意见的修正矩阵，而且一致性检验和调整过程比较简单。
Algorithm 1. Two-stage consistency adjustment algorithm
算法1. 两阶段一致性调整算法
例：
计算得CI = 0.1490，CR = 0.1655 > 0.1，需要调整。计算矩阵A的完全一致矩阵
，
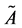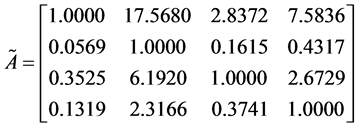。计算得
，
。
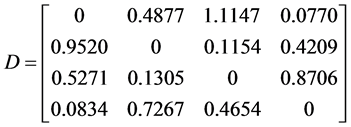矩阵D中偏离距离大的是d13 = 1.1147，修改偏离距离最大的元素a13 = 6。根据矩阵B，由于b13 > 1，修改后a13的值应该缩小为[1/9, 1/8, 1/7, 1/6, 1/5, 1/4, 1/3, 1/2, 1, 2, 3, 4, 5, 6, 7, 8, 9]中的一个相邻区间值，取a13 = 5。得出修正矩阵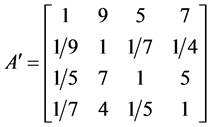
。计算得出CI = 0.1259，CR = 0.1398 > 0.1，仍需要调整。同理，再次计算完全一致性矩阵
和矩阵B、矩阵D，最终得到修正矩阵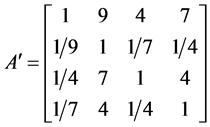
。计算得CI = 0.0840，CR = 0.0933<0.1，满足要求。修正矩阵A'满足一致性，并最大程度地保留了专家的原始意见。
3.3. 通信指挥效能评估算例
通信指挥过程中往往预设多种方案，通过评估选择最有效的方案执行。图1展示了通信指挥效能评
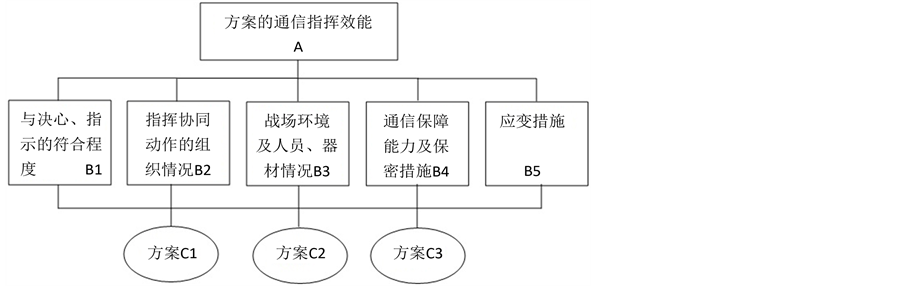
Figure 1. Structure table of communication and command effectiveness evaluation
图1. 通信指挥效能评估结构图
估结构图。
通信指挥效能与多种因素有关，根据专家建议选取以下方面。(1) 方案与领导的决心、上级的指示的符合程度；(2) 方案指挥协同各战斗部门的组织情况；(3) 方案考虑战场环境和人员、设施器材的情况；(4)方案预设的通信保障能力和保密措施；(5) 方案应对突发状况的应变措施。预设有三种方案可供选择。
专家两两比对B1~B5五种策略的重要程度形成决策判断矩阵A。
计算得CI = 0.1286，CR = 0.1148 > 0.1，需要调整一致性。根据矩阵A计算出完全一致性矩阵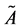
：
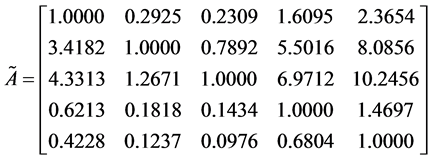。计算偏差比例矩阵B和偏差距离矩阵D：
，
。
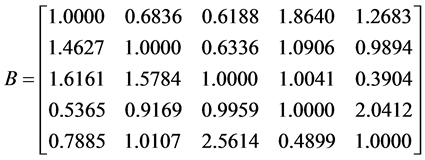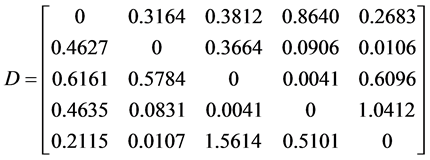通过两阶段一致性算法获得调整后的修正矩阵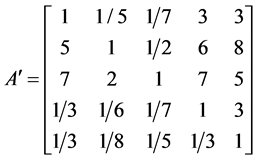
，计算矩阵A'一致性得CI = 0.1065，CR = 0.0951 < 0.1，满足一致性并最大程度符合专家原始意见。计算W = (0.1021, 0.3311, 0.4603, 0.0639, 0.0427)T，特征向量λmax = 5.4258。
分析不同方案对五种准则的重要程度。根据专家两两比较,构造三个五阶矩阵：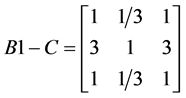
，
，
，
，
。
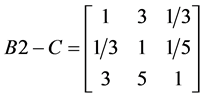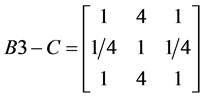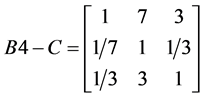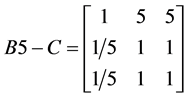按照上面介绍的步骤计算，检验判断矩阵的一致性，获得指标层各指标下三个方案的最大特征根、权重向量分别为：
;
;
;
;
。
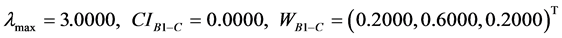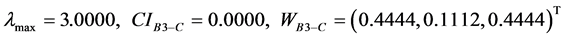方案层的三个方案C1、C2、C3对目标A的权重向量根据公式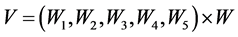
,可得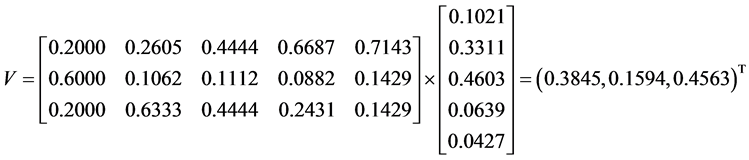
。则这三种方案对目标的权重分别为0.3845，0.1594，0.4563，根据结果评估出三种方案通信指挥效能由强到弱的顺序为C3，C1，C2。
4. 结论
本文介绍了一种自动调整层次分析法中判断矩阵一致性的方法，在此基础上对通信指挥效能进行评估。对不满足一致性的判断矩阵，采用两阶段调整方法。第一阶段，构造一致性矩阵，计算原判断矩阵中与一致性矩阵相比偏差最大的元素；第二阶段，定义调整规则，迭代修改与一致性矩阵偏差最大的原矩阵元素。本文通过求解通信指挥效能评估问题算例，对所提方法进行验证，结果证明本文方法方便高效，且求解结果能最大程度保留原专家意见。
基金项目
基于情景探索的非常规突发事件中非战争军事行动应急计划方法研究(91024006)。