碳排放与其影响因素之间关系的变化—基于STIRPAT模型的分位数回归分析

The Change of the Relationship between CO₂ Emissions and the Driving Forces—Quantile Regression Based on STIRPAT Model

摘要: 前人很多有关人口、财富、科技和碳排放的关系的研究，都假定人口和财富的生态弹性系数是时间不变和空间不变的。本文基于STIRPAT模型，利用稳健的分位数回归分析了，我们讨论了碳排放与人口、财富和科技的关系在1992~2009年期间的变化情况。主要结果如下：1) 对于财富的生态弹性系数比人口的生态弹性系数大的国家，人口、财富、科技和碳排放的STIRPAT关系变化很小。2) 对于碳排放量相对高的国家，人口是碳排放的主要因素，科技对碳排放总量的影响也大，而碳排放量越高，财富对碳排放的影响越小。3) 对于碳排放量很高的国家，财富的生态弹性系数介于0.65~1.1之间。对于碳排放量较低或很低的国家，财富的生态弹性系数稳定在1.2附近。4) 9个不同分位数回归的科技截距的变化幅度由1992年的8.5缩小到2009的2.8。

Abstract: In most previous studies of the relationship between CO₂ emissions, population, affluence and technology, the ecological elasticities of population and affluence were assumed to be both time invariant and space invariant. Based on the STIRPAT model, by using robust quantile regression, we studied the change of the relationship between CO₂ emissions, population, affluence and technology at different CO₂ emissions levels during the period 1992-2009. Our main results are as follows: 1) the relationship between CO₂ emissions, population, affluence and technology changes slightly in countries where the ecological elasticity of affluence is greater than that of the population. 2) In those countries with relatively high levels of CO₂ emissions, higher emissions mean that increases in population and affluence have smaller effects on the impacts of emissions, but technology has a greater effect on those impacts. 3) In those countries with high CO₂ emissions, the ecological elasticity of affluence increases from less than 0.65 to 1.1, but in countries with moderate or low CO₂ emissions, the ecological elasticity of affluence is stable at approximately 1.2. 4) The shifting scope of the technology intercepts of nine different quantile regression analyses decreases from 8.5 in 1992 to 2.8 in 2009.

1. STIRPAT模型

温室气体(GHGs)在大气层加速聚集是公认的现象，而温室气体的持续增加将导致地球气候变暖 [1] 。人类活动是温室气体增加的直接原因已得到科学界的广泛认同。在这些人为因素中，温室气体排放的主要驱动因素包括人口数量、经济活动、科技、政治和经济机构、人的生活习惯和宗教信仰 [2] 。这些驱动因素以何方式影响温室气体排放并导致人类环境变化是一个非常重要的课题。IPAT方程 [3] 正是这个课题研究的重要成果。

IPAT方程最早出现在上世纪70年代，Ehrlich-Holdren和Commoner讨论人类环境影响的主要驱动因素，该方程假设对环境的影响(I)是人口(P)，人均GDP(A)和科技(T)的乘积。IPAT方程这种乘积结构广泛地用于环境变化的驱动因素分析(参见文 [4] - [6] )。1994年，Dietz和Rosa [7] 将IPAT方程改成随机形式，即STIRPAT模型：

(1)

其中，科技项(T)不仅包括科技还包括社会组织形式，文化等除人口和财富之外的所有其它人为因素。STIRPAT模型(1)虽然保留了IPAT方程的乘积结构，但相比IPAT方程更便于检验假设和精细分析。为了做假设检验，一般将方程(1)转化成下列自然对数形式：

(2)

其中a和e分别为方程(1)中a和e的自然对数。方程(2)中的参数均可针对截面数据，时间序列数据或面板数据，利用传统的统计技术比如回归方法来估计。其中驱动因素系数b，c称为生态弹性(参见文 [8] )，它们体现了个驱动因素的弹性，即当其它驱动因素不变时，某驱动因素变化一个百分点，环境影响I变化的百分比。模型(2)由文 [2] 首次提出，现已广泛用于生态足迹，能源足迹，CO₂排放以及其它环境污染物排放的驱动因素分析，利用的数据类型有截面数据，时间序列数据或面板数据(参见 [2] [8] - [12] )。

在这个乘积结构中，当驱动因素变化细微时，生态弹性系数能起重要的作用。然而当环境的某驱动因素变化较大时，我们不必利用弹性系数而直接分析驱动因素本身就足够了。比如本文的结果显示碳排放相对高的国家，其科技项的变化非常显著，因此没有必要考察科技的生态弹性系数。

比较方程(2)和方程(1)，会发现方程(2)缺了科技项(T)。York等在文 [8] 指出科技项包含了除开人口和财富之外的其它所有驱动因素，因此科技项包含在残差项中。York等在他们的一系列文章(参见文 [6] [8] [10] [13] )中都直接将残差项当作科技项的对数，而参数a一直没有合理的解释。由于残差以零为均值，这样蕴含着科技的弹性系数期望恒为零，相应的科技乘子exp(e)的均值恒为1。本文将STIRPAT模型(2)中参数a的指数值当作科技乘子，而将参数a称为科技截距。科技截距小，意味着科技对环境影响的贡献小。

在有关STIRPAT模型(2)的大量文献中，学者们一般将其用于全球环境变化的人为驱动因素的效用分析。很多应用都假定人口和财富的生态弹性系数是时间和空间不变的(参见文 [14] [15] )。在近十来年，有很多学者利用面板回归技术(参见文 [9] [16] [17] )。然而，面板回归模型一般包含个体固定效应、时间固定效应等，最终得到的是因变量和自变量在数学期望意义下的平均关系。例如，STIRPAT模型(2)的一种面板数据形式如下

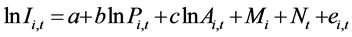
下标i代表国家，下标t代表年份，而和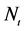分别表示国家和时间虚拟变量。若用面板回归技术估计参数b和c，蕴含人口和财富的生态弹性系数在空间和时间上是不变的。而虚拟变量和的差异只是体现包括科技在内的其它驱动因子在空间或时间上的差异。这种STIRPAT面板模型并不能反映人口和财富对碳排放的影响在空间和时间上变化情况。

为了确定在不同国家中碳排放与人口、财富和其它驱动因素之间的关系，有些学者根据各种标准比如收入水平、地区差异，将观察国家分成若干类，再分别应用面板回归，得到各种STIRPAT面板模型。正如所期望的，不同类的模型参数结果不同，参见文 [8] [9] [14] [16] [17] 。本文将各观察国家和地区按碳排放总量进行排序，利用分位数回归，分析不同碳排放量的国家和地区的碳排放STIRPAT模型，由此分析人口、财富和科技对碳排放影响的变化情况。

2. 分位数回归

回归分析从1886年被高尔顿首次使用以来，已广泛应用于生物，医学，金融，经济等各个领域中的数据分析，其中以基于最小二乘法的经典线性回归(LSR)在数据分析中应用最广。但这种条件期望模型有其自身的缺陷：a) 随机误差需要几个比较苛刻的假设(包括零均值、等方差、正态分布等)；b) 对异常值敏感，尤其当样本量较小和误差分布厚尾时；c) 只是确定在条件期望意义下的总体函数关系，不能体现分布的各部分的函数关系。

为了弥补经典线性回归的缺陷，1978年，Koenker和Bassett在文 [18] 中提出了分位数回归(Quantile Regression, QR)。

设随机变量的分布函数为，则的第分位数为。对于的一组随机样本，样本均值是的最优解，而样本分位数是的解。其中损失函数为分段线性函数，为示性函数。

对于回归模型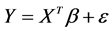，其中为随机变量。为了分析自变量对因变量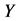在其各分位数的影响，即获得因变量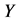在其各分位数关于自变量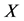的线性函数关系，需求解，其等价于求解

由于分位数回归计算的复杂性，早期它没能象经典的回归分析那样迅速普及。现在随着分位数回归理论研究的不断完善以及计算机技术的快速发展，分位数回归的应用越来越广，很多主流统计软件如SAS、Eviews、R等都有相应的功能模块。

3. 数据与方法

本文，我们针对STIRPAT 模型(2)应用稳健的分位数回归分析碳排放与人口、财富和其它驱动因素之间的关系。面板数据来自世界银行集团网站www.worldbank.org，由各国家在1992~2009年期间各年的CO₂排放量、国家人口总数、人均国内生产总值构成。实际人口数据以百万为单位。人均国内生产总值是按当年的的购买力折算成2005年的数值，以国际货币美元为单位。CO₂排放量数据，以千吨为单位，是根据化石燃料和水泥的使用量按各自的比例折算出来的数值，包含消耗固态、液态、气态燃料和天然气燃烧产生的CO₂。排除人口总数小于100万的和1992~2009年期间数据不齐全的国家(地区)，最后得到由127个国家和地区18年的CO₂排放量、国家人口总数、人均国内生产总值构成面板数据集。这127国家和地区及其编号如表1所示。

为了表现CO₂排放与其驱动因素之间的线性函数关系在时间和空间上的变化情况，我们针对每一年的数据，分别在9个分位点上用分位数回归方法估计STIRPAT 模型(2)的参数，即求解

其中下标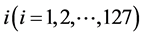表示127个国家(地区)。

为了比较，我们同时还使用最小二乘法估计STIRPAT模型(2)的参数。所有这些估计均由软件The Eviews 6.0实现，结果如表2和图1~图3所示，其中(LCI, UCI)为LSR的95%置信区间。

4. 结果分析

由最小二乘法以及9个分位点的分位数回归得到的人口和财富的生态弹性系数以及科技截距由表2和图1~图3展示。基于最小二乘法的经典线性回归结果表明，总体人口弹性系数稳定在处，财富生态弹性系数稳定在处，而科技截距稳定在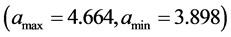处。另一方面，人口生态弹性系数比财富生态弹性系数小，这与文 [19] 的结果相同，而与文 [2] 的结果相反。造成这种截然相反的结果很有可能是文 [2] 假定了生态弹性系数是时间不变的且使用的数据并非全都来自1989年。

Table 1. 127 Countries and their sample numbers

表1. 127个国家(地区)及其序号

Table 2. Results of LSR and QR

表2. LSR和QR结果

Figure 1. Ecological elasticity curves for population

图1. 人口的生态弹性系数曲线

Figure 2. Ecological elasticity curves for affluence

图2. 财富的生态弹性系数曲线

Figure 3. Technology intercept curves

图3. 科技截距曲线

分位数回归结果显示，财富的生态弹性系数比人口的生态弹性系数大的国家(对应于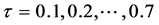)在1992~2009年期间，人口弹性系数、财富生态弹性系数和科技截距的变化很小。人口的生态弹性系数在分位点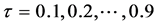的值几乎都落在由最小二乘法估计得到的b值的95%的置信区间内。由表2还可以看出基本上满足关系。这表明CO₂排放量相对高的国家，CO₂排放量越高人口的生态弹性系数越小。财富的生态弹性系数在分位点处的值几乎都落在由最小二乘法估计得到的c值的95%的置信区间内。而在分位点处和处在大部分时间内(2001年前)位于由最小二乘法估计得到的c值的95%的置信区间之外。由表2可以看出基本上满足关系。这表明CO₂排放量相对高的国家，CO₂排放量越高财富的生态弹性系数越小。科技截距在分位点处的值几乎都落在由最小二乘法估计得到的a值的95%的置信区间之外，而且在1992~2009年期间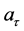，是的严格增函数，这表明CO₂排放量高的国家，科技对CO₂排放的影响越大。更为重要的是，随时间的推移，科技截距在9个不同分位点上的变化幅度越来越小，变化幅度由1992年的8.5缩小到2009的2.8。

以上分析表明，经典的最小二乘法估计得到STIRPAT模型并不能代表所有观察国家和地区的情况，利用分位数回归方法获得的不同STIRPAT模型更能细致地反应不同国家的碳排放与其影响因素之间的关系。另外，不同国家和地区的财富生态弹性系数和科技截距的趋同现象从一定程度体现了21世纪世界各国在经济、科技和文化活动等各领域的交流合作越来越多，联系越来越紧密。

基金项目

本文获得教育部人文社科基金(批准号：11YJA790190)和湖南省自科基金(批准号：2016JJ6029)资助。