1. 引言
非线性频率变换是光与物质相互作用的参量过程,其材料的量子态不变,即光场与物理系统之间没有能量、动量或角动量的转换。过去几十年,随着新型非线性晶体材料的研究,非线性频率变换在激光技术中得到飞速发展。自1961年Franken等人首次发现二次谐波以来 [1] ,和频、差频、三次谐波和四波混频等参量过程相继被发现,成为产生不同频谱的有效方法。1995年,Kwiat等人利用BBO晶体产生高效偏振纠缠光子 [2] ,自此,在非线性晶体中利用参量下转换方法成为产生纠缠光子的主要手段,如,LBO [3] ,KDP [4] ,BBO [5] , KTP [6] 以及半导体材料 [7] 等,使得纠缠光子的产生效率得到很大提高。在此基础上,新型晶体PPLN [8] 以及BIBO [9] [10] 等的应用,将非线性频率变换技术在量子光学领域得到进一步推广。
影响非线性参量下转换效率的两个重要因素是晶体的非线性系数和相位匹配条件。在实际参量下转换过程中,由于不同波长光的折射率不同,在晶体内传播具有不同的速率和传输路径,存在色散和时间空间走离 [11] [12] ,因而非线性转换效率难以提高。目前,常用的双折射相位匹配(BMP)技术是通过选择波矢方向和偏振方向来实现的。在超快激光泵浦情况下,光束色散导致泵浦峰值功率降低,使得参量下转换效率难以提高。另外,晶体的各向异性使得自发参量下转换过程产生的纠缠光子对呈现不对称空间分布 [13] ,影响纠缠光子的纠缠度。在双轴晶体特别是斜方晶体中,这种不对称的窄化滤波作用更加明显,可以将空间发散严重的宽带差准直泵浦光束整形为窄带小发散角的超细光束,提高光子的纠缠度。由于斜方晶系的结构复杂,在非线性相位匹配条件的计算难度很大。目前,关于双轴晶体中相位匹配参数的计算普遍采用姚建铨的方法,该方法将双轴晶体等效为单轴晶体,然后求解菲涅尔方程 [14] [15] ,非常复杂。若能够找到一种在双轴晶体中计算相位匹配条件的简便方法,对非线性光学和量子光学领域都具有重要理论和实际意义。
本文针对斜方晶系晶体在非线性频率变换中的相位匹配问题,提出了一种基于角度计算的相位匹配方法。该方法利用日本数学家小平邦彦对角度概念的推广,通过角度投影的方法,确定了光波矢量和两光轴与之间夹角与相位匹配角之间的关系。折射率通过角度直接计算,避免了求解二阶菲涅尔方程,获得相位匹配条件更为便捷。文章以单斜晶体BIBO的自发参量下转换过程为例,获得了I和II类相位匹配的角度关系和有效非线性系数,进一步结合自发参量下转换和倍频过程的对比讨论了角度表象下折射率梯度的物理意义。
2. 角度计算
在介电主轴坐标系(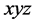 )下,依据波法线菲涅尔方程可以计算光沿任意方向传输的折射率,而晶体参数是在晶体主轴坐标(abc)下测得。在斜方晶系中,这两个坐标系统之间并不是完全平行的。为了获得折射率与角度之间的关系,先将介电主轴坐标(
)下,依据波法线菲涅尔方程可以计算光沿任意方向传输的折射率,而晶体参数是在晶体主轴坐标(abc)下测得。在斜方晶系中,这两个坐标系统之间并不是完全平行的。为了获得折射率与角度之间的关系,先将介电主轴坐标(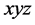 )沿z轴旋转
)沿z轴旋转 角,再将坐标
角,再将坐标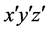 沿
沿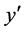 轴旋转
轴旋转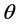 角,得到实验室坐标
角,得到实验室坐标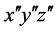 ,如图1所示。这里
,如图1所示。这里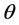 是
是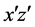 面内相对于介电主轴z偏转的极角,
面内相对于介电主轴z偏转的极角,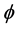 是
是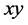 面内相对于介电主轴x的方位角。两光轴C1,C2对称地分布于z轴两侧,且与z轴之间的夹角分别为
面内相对于介电主轴x的方位角。两光轴C1,C2对称地分布于z轴两侧,且与z轴之间的夹角分别为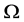 和
和 。
。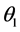 和
和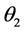 是波矢量k与两光轴C1,C2之间的夹角,
是波矢量k与两光轴C1,C2之间的夹角,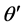 和
和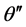 则分别是波矢量k在
则分别是波矢量k在 面、
面、 面的投影与z轴之间的夹角。
面的投影与z轴之间的夹角。
根据波法线菲涅尔方程,可得光束的两正交特许线偏振光的折射率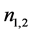 为 [16]
为 [16]
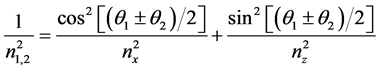 (1)
(1)
取正负号便可得两个折射率
 ( 2a )
( 2a )
 (2b)
(2b)
其中,光轴角 可表示为 [17]
可表示为 [17]
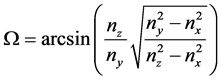 (3)
(3)
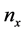 ,
,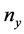 ,
,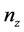 是三个主轴折射率。若公式(2)中的角度
是三个主轴折射率。若公式(2)中的角度 和
和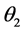 已知,则两个折射率可以计算出来直接应用到相位匹配条件。
已知,则两个折射率可以计算出来直接应用到相位匹配条件。
下面利用日本数学家小平邦彦对角度定义的推广 [18] ,通过角度投影法计算角度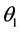 和
和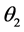 与
与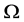 ,
,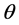 和
和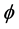 之间的关系。首先将波矢量k (
之间的关系。首先将波矢量k (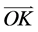 )及线段
)及线段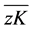 分别投影到yz, xz平面内,得到
分别投影到yz, xz平面内,得到 ,
,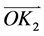 ,
,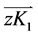 和
和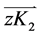 。
。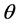 可表示为
可表示为
 (4)
(4)
由于线段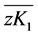 是
是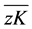 在yz面的投影,则直角三角形zK1K满足关系
在yz面的投影,则直角三角形zK1K满足关系
 (5)
(5)
而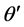 角可表示为
角可表示为
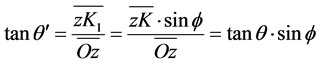 (6)
(6)
在四面体O-C2zK1中,根据三角余弦关系有
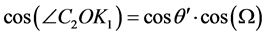 (7)
(7)
其中,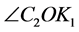 是OC2和OK1之间的夹角。而
是OC2和OK1之间的夹角。而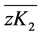 是
是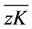 在xz面的投影,则在直角三角形zK2K中满足关系
在xz面的投影,则在直角三角形zK2K中满足关系
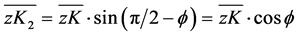 (8)
(8)
xz面内的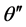 角满足
角满足
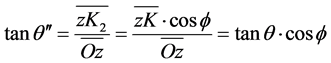 (9)
(9)
根据四面体O-C1zK2中的三角余弦关系
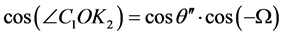 (10)
(10)
其中, 是OC1和OK2之间的夹角。从图1的几何关系,能够得到
是OC1和OK2之间的夹角。从图1的几何关系,能够得到
 ( 11a )
( 11a )
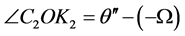 (11b)
(11b)
与上述过程类似,在四面体O-KK2z内根据余弦关系得到
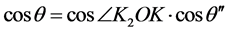 (12)
(12)
一般条件下,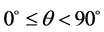 且
且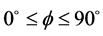 ,在四面体O-KK
2 C
1和O-KK
2 C
2内,根据三角余弦关系有
,在四面体O-KK
2 C
1和O-KK
2 C
2内,根据三角余弦关系有
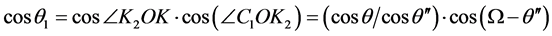 (13)
(13)
 (14)
(14)
其中, 。当
。当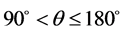 及
及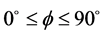 时,取
时,取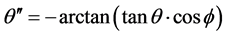 ,当
,当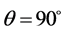 ,
,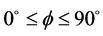 时,由公式(13)和(14)得到
时,由公式(13)和(14)得到
 (15)
(15)
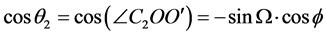 (16)
(16)
公式(13)-(16)就是介电主轴坐标(xyz)和实验室坐标(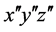 )之间的角度转换关系,
)之间的角度转换关系,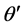 和
和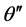 是
是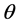 在
在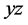 面和
面和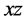 面的投影。当参数
面的投影。当参数 ,
, 和
和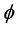 已知时,可以得到角度
已知时,可以得到角度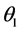 和
和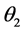 的大小,然后由公式(1)得到两个折射率
的大小,然后由公式(1)得到两个折射率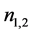 。
。
如果光轴角 ,就有
,就有 ,如图2所示。斜方的双轴晶体等效为单轴晶体。公式(1)简化为
,如图2所示。斜方的双轴晶体等效为单轴晶体。公式(1)简化为
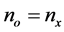 和
和 (17)
(17)
其中,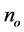 和
和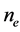 就是单轴晶体中寻常光和异常光的折射率,
就是单轴晶体中寻常光和异常光的折射率,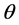 是波矢量k与光轴之间的夹角。所以单轴晶体属于双轴晶体的特殊情况,同样满足上述推导的角度关系。
是波矢量k与光轴之间的夹角。所以单轴晶体属于双轴晶体的特殊情况,同样满足上述推导的角度关系。
前述角度计算方法是在单斜晶系中展开,也可以拓展到三斜晶系,如图3所示。三斜晶系的三晶轴a,b,c之间均不垂直,若将图3中的b轴也做一次类似的投影分解,分解为垂直和平行于b、c晶轴构成平面的线段。根据三角余弦关系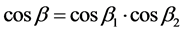 求解角度,便可获得三斜晶系中利用参数
求解角度,便可获得三斜晶系中利用参数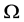 ,
,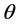 和
和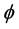 表示
表示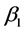 和
和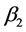 的关系式。进一步借助前述式(1)-(3)可以求得三斜晶系的折射率。
的关系式。进一步借助前述式(1)-(3)可以求得三斜晶系的折射率。

Figure 2. The angle relations in monolithic crystal for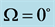
图2.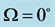 时单斜晶体中的角度关系
时单斜晶体中的角度关系
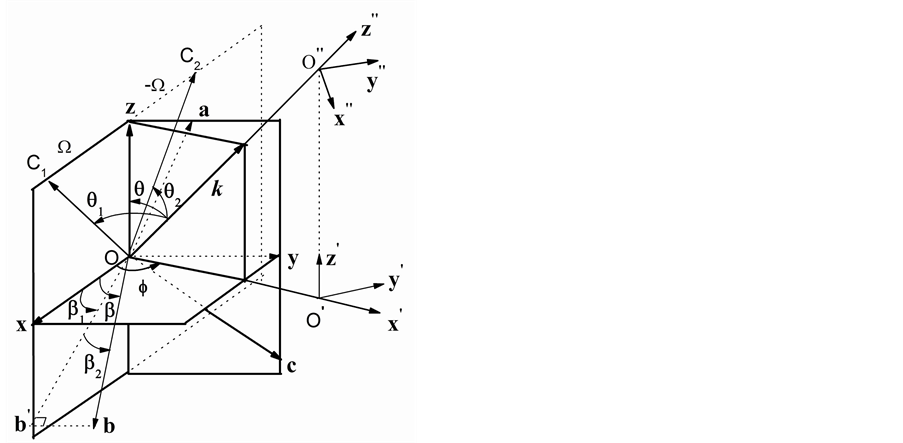
Figure 3. The angle relations and axial projection in triclinic crystal
图3. 三斜晶体的角度关系与晶轴投影
3. 角度表象下的相位匹配
非线性参量过程中,相位匹配条件对输出光的转换效率至关重要。双轴晶体中的相位匹配条件较单轴晶体尤为复杂,目前关于这一问题求解均需求解菲涅尔方程。这里,我们利用前面推导的双轴晶体中角度关系,直接应用折射率的相位匹配条件,避免复杂的分析和求解过程。相位匹配条件下的非线性频率变换,入射光和出射光满足能量和动量守恒定律,可表示为
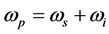 ( 18a )
( 18a )
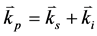 (18b)
(18b)
上式中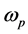 ,
,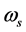 ,
,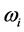 为泵浦光频率,信号光频率,闲频光频率,
为泵浦光频率,信号光频率,闲频光频率,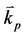 ,
, ,
,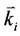 则分别为泵浦光、信号光和闲频光的波矢量。由于晶体的双折射效应,每束光在晶体内均以快光(fast)或慢光(slow)形式传输,相应的折射率表示为
则分别为泵浦光、信号光和闲频光的波矢量。由于晶体的双折射效应,每束光在晶体内均以快光(fast)或慢光(slow)形式传输,相应的折射率表示为 ,
,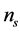 ,公式(18b)有下面两种形式
,公式(18b)有下面两种形式
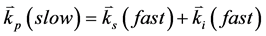 ( 19a )
( 19a )
 (19b)
(19b)
公式(19a)为一类相位匹配,而公式(19b)为二类相位匹配。
在简并参量下转换相位匹配条件下,一个入射光子分裂为一对频率相等的低能量相关光子(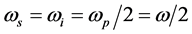 ),满足公式(18)的能量和动量守恒定律。为表示方便起见,将波矢量表示为
),满足公式(18)的能量和动量守恒定律。为表示方便起见,将波矢量表示为 (l = p, s, i),其中
(l = p, s, i),其中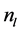 为光子折射率,
为光子折射率,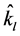 为单位矢量,
为单位矢量,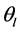 ,
, 为对应的极角和方位角。在共线情况下,两类相位匹配条件简化为折射率形式
为对应的极角和方位角。在共线情况下,两类相位匹配条件简化为折射率形式
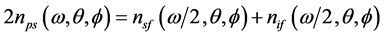 ( 20a )
( 20a )
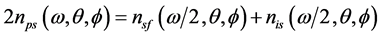 (20b)
(20b)
其中,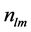 (l = p, s, i; m = slow, fast) 为基波和下转换光波所对应的折射率。利用公式(2)给出的折射率代入上式,可以得到相位匹配角度关系
(l = p, s, i; m = slow, fast) 为基波和下转换光波所对应的折射率。利用公式(2)给出的折射率代入上式,可以得到相位匹配角度关系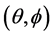 ,并以此为基础可以计算其他相位匹配参数。
,并以此为基础可以计算其他相位匹配参数。
以单斜晶系的BIBO晶体为例,将公式(13)和(14)的角度关系代入公式(2)得到快光和慢光的折射率,然后代入公式(20),可以得到一类和二类相位匹配条件下的角度关系。利用室温条件下的晶体参数,数值模拟公式(20)参量下转换过程的相位匹配条件,得到泵浦光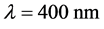 的I类相位匹配关系,如图4(a)所示;泵浦光
的I类相位匹配关系,如图4(a)所示;泵浦光 的II类相位匹配关系,如图4(b)所示。
的II类相位匹配关系,如图4(b)所示。
以图4相位匹配角度关系为基础,可以进一步获得有效非线性系数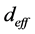 等其他相位匹配参数。例如,以BIBO晶体为例,I类、II类相位匹配条件下有效非线性系数与相位匹配角
等其他相位匹配参数。例如,以BIBO晶体为例,I类、II类相位匹配条件下有效非线性系数与相位匹配角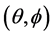 的关系分别为 [19] [20]
的关系分别为 [19] [20]
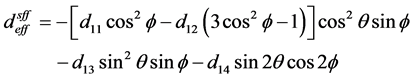 ( 21a )
( 21a )
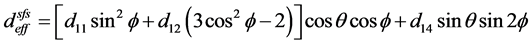 (21b)
(21b)
其中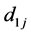 (j = 1, 2, 3, 4) 为矩阵张量系数。
(j = 1, 2, 3, 4) 为矩阵张量系数。
取晶体参数 ,
,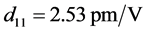 ,
,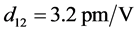 ,
,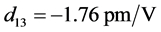 以及
以及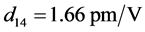 ,利用图4的相位匹配角度关系,数值模拟公式(21)得到I类和II类相位匹配条件下有效非线性系数随角度的变化关系,如图5所示。图5(a)描述了I类相位匹配条件下泵浦光
,利用图4的相位匹配角度关系,数值模拟公式(21)得到I类和II类相位匹配条件下有效非线性系数随角度的变化关系,如图5所示。图5(a)描述了I类相位匹配条件下泵浦光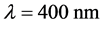 时,
时,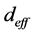 与
与 ,
,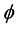 之间的变化关系。而图5(b)描述了II类相位匹配条件下泵浦光
之间的变化关系。而图5(b)描述了II类相位匹配条件下泵浦光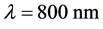 时,
时,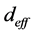 与
与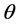 ,
,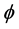 之间的变化关系。从该图可以确定BIBO晶体的最佳相位匹配方向,确定晶体的切割角度和泵浦光的入射方向。这些结果与之前采用姚建铨方法取得的结果是一致的。
之间的变化关系。从该图可以确定BIBO晶体的最佳相位匹配方向,确定晶体的切割角度和泵浦光的入射方向。这些结果与之前采用姚建铨方法取得的结果是一致的。
4. 角度表象下折射率的优势
角度表象下的折射率可以直接应用于相位匹配计算,简捷方便。现在以图6所示的斜方晶体中I类共线简并相位匹配进行说明。图中B点是两折射率椭球交叠位置之一,满足相位匹配条件。假如激光沿OB线方向传输,下转换光束在该线附近存在弥散。在傍轴和宽晶体近似条件下,对折射率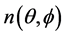 进行零阶和一阶泰勒展开,得到线性失配量
进行零阶和一阶泰勒展开,得到线性失配量
 (22)
(22)
其中
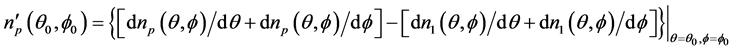 (23)
(23)
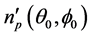 是
是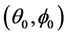 点的折射率梯度,线性失配
点的折射率梯度,线性失配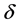 不为零。这里,泵浦光的折射率角梯度
不为零。这里,泵浦光的折射率角梯度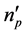 接近最佳相位匹配方向
接近最佳相位匹配方向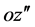 ,且其绝对值
,且其绝对值 可看作椭球的离心率。对于BIBO晶体的I类自发参量下转换过程,
可看作椭球的离心率。对于BIBO晶体的I类自发参量下转换过程,
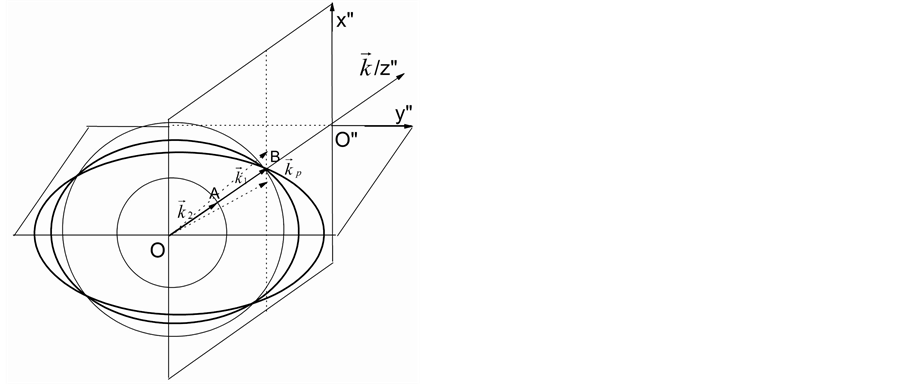
Figure 6. The optimal phasing matching of collinear parameter process in orthorhombic crystal
图6. 斜方晶体中共线参量过程中最佳相位匹配情况
 在
在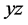 面内具有最大值,(23)式的第二部分为零,其绝对值达到最大值。对于斜方晶体的两个折射率曲面变为一个椭球和一个圆球,恰如单轴晶体中参量下转换的
面内具有最大值,(23)式的第二部分为零,其绝对值达到最大值。对于斜方晶体的两个折射率曲面变为一个椭球和一个圆球,恰如单轴晶体中参量下转换的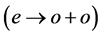 情况,倍频过程中
情况,倍频过程中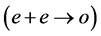 ,折射率梯度
,折射率梯度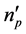 获得最大值。换句话说,若要得到BIBO晶体的I类最佳相位匹配,泵浦光沿着椭球,而下转换光或倍频光就必须沿着圆球。可以看出,借助角度表象下的折射率很容易确定相位匹配角,而且可以直接地确定泵浦光和转换光传输路径。
获得最大值。换句话说,若要得到BIBO晶体的I类最佳相位匹配,泵浦光沿着椭球,而下转换光或倍频光就必须沿着圆球。可以看出,借助角度表象下的折射率很容易确定相位匹配角,而且可以直接地确定泵浦光和转换光传输路径。
5. 结论
本文介绍了一种在双轴晶体中计算相位匹配参数的简单方法。通过角度投影的方法推导两个光轴与波矢量夹角之间的关系,得到角度表象下折射率的解析表达式,该折射率表达式可直接应用于相位匹配条件。文章以BIBO晶体的自发参量下转换过程为例,计算了I类、II类相位匹配条件下的角度关系和有效非线性系数。通过对比自发参量下转换过程和倍频过程,讨论角度表象下折射率梯度的物理意义。该相位匹配方法的计算避免了求解菲涅尔方程,使双轴晶体中相位匹配参数的计算更为便捷。
基金项目
陕西省教育厅项目(No. 16JK2247), 西京学院高层次人才专项基金(No. XJ15B02)。
NOTES
*通讯作者。