1. 引言
求解非线性发展方程是非线性理论的一个重要课题,迄今为止,学者们已经利用Painlevé分析法 [1] [2] 、Bäcklund变换法 [3] 、辅助方程法 [4] 、G'/G—展开法 [5] 等对非线性发展方程进行了求解。受G'\G—展开法的启发,近来学者们又提出“修正的简单方程法 [6] [7] ”并对Fitzhugh-Nagumo方程和Sharma-Tasso- Olver方程等许多常系数非线性发展方程进行精确求解。但目前为止未见用此方法来求解该方法无法直接运用的方程,如sine-Gordon方程 [8] [9] 以及变系数非线性发展方程。故本文旨在利用该方法给出sine- Gordon方程和广义的变系数KdV-mKdV方程 [10] 的精确行波解。
sine-Gordon方程在非线性光学、等离子物理、固体物理等自然科学领域中有着广泛的应用;在流体力学和等离子体中,广义变系数非等谱KdV-mKdV方程用来刻画弱非线性长波在KdV介质中传播,因此这两个方程都是有重要物理背景的模型方程。因此寻找sine-Gordon方程和广义的变系数KdV-mKdV方程的精确解在理论和实际应用中有着至关重要的意义。
2. sine-Gordon方程
下面考虑用修正的简单方程法求解sine–Gordon方程
 (2.1)
(2.1)
的问题。为此作变换
 ,则
,则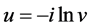 (2.2)
(2.2)
则可将方程(2.1)转化为
 (2.3)
(2.3)
再作行波变换
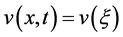 ,
,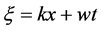 (2.4)
(2.4)
并将(2.4)代入(2.3)得到
 (2.5)
(2.5)
利用齐次平衡原则,平衡(2.5)中的最高阶导数项v³和非线性项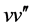 和
和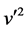 ,知n = 2,故可设
,知n = 2,故可设
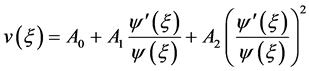 ,
,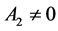 (2.6)
(2.6)
把(2.6)代入(2.5)后比较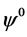 ,
, ,
,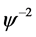 ,
,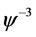 ,
,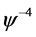 ,
,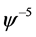 ,
,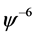 的系数可得
的系数可得
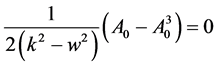 (2.7)
(2.7)
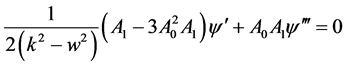 (2.8)
(2.8)
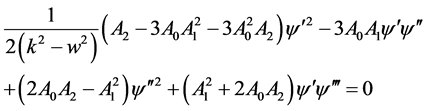 (2.9)
(2.9)
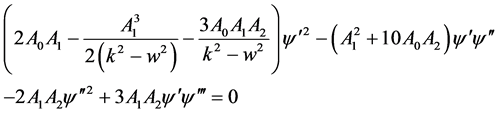 (2.10)
(2.10)
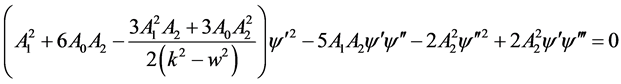 (2.11)
(2.11)
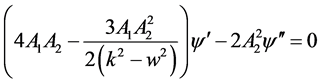 (2.12)
(2.12)
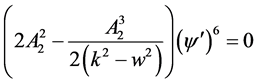 (2.13)
(2.13)
由(2.7)可得: ;由(2.13)可得:
;由(2.13)可得: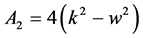
1) 当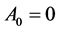 时,(2.5)无(2.6)形式的解
时,(2.5)无(2.6)形式的解
2) 当 时,(2.8)~(2.12)化为常微分方程组
时,(2.8)~(2.12)化为常微分方程组
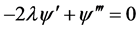 (2.14)
(2.14)
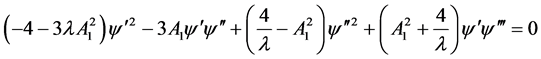 (2.15)
(2.15)
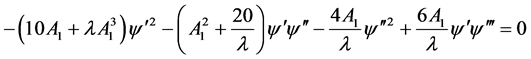 (2.16)
(2.16)
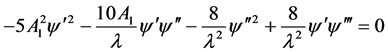 (2.17)
(2.17)
 (2.18)
(2.18)
其中: ,
,
由(2.18)可得
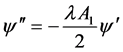 ,则
,则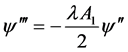 (2.19)
(2.19)
把(2.19)代入(2.14)可得
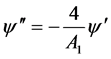 ,则
,则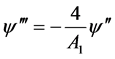 (2.20)
(2.20)
把(2.20)代入(2.15)可得
 ,则
,则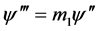 ,
, (2.21)
(2.21)
把(2.21)代入(2.16)可得
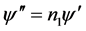 ,则
,则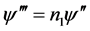 (2.22)
(2.22)
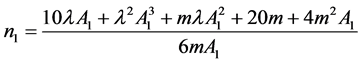 (2.23)
(2.23)
把(2.22)代入(2.17)可得
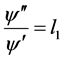 ,
, (2.24)
(2.24)
对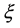 积分两次有
积分两次有
 (2.25)
(2.25)
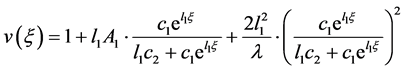 (2.26)
(2.26)
因此
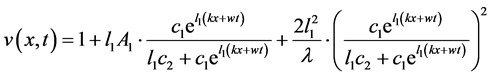 (2.27)
(2.27)
从而
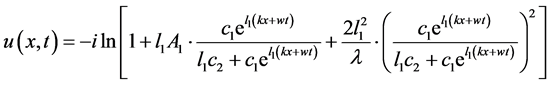 (2.28)
(2.28)
取 ,
,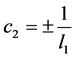 ,得到sine-Gordon方程的精确孤波解
,得到sine-Gordon方程的精确孤波解
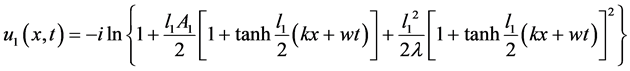 (2.29)
(2.29)
 (2.30)
(2.30)
3) 当 时,(2.8)~(2.12)化为常微分方程组
时,(2.8)~(2.12)化为常微分方程组
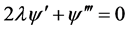 (2.31)
(2.31)
 (2.32)
(2.32)
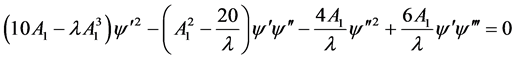 (2.33)
(2.33)
 (2.34)
(2.34)
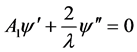 (2.35)
(2.35)
完全类似于方程组(2.14)~(2.18)的求解过程,我们得到
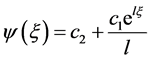 ,
, (2.36)
(2.36)
 ,
,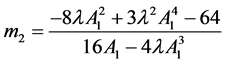 (2.37)
(2.37)
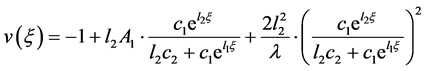 (2.38)
(2.38)
因此
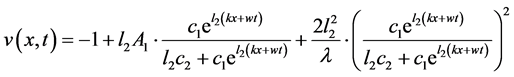 (2.39)
(2.39)
从而
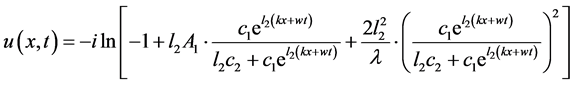 (2.40)
(2.40)
取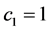 ,
,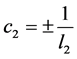 ,得到sine-Gordon方程的精确孤波解
,得到sine-Gordon方程的精确孤波解
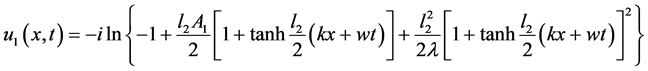 (2.41)
(2.41)
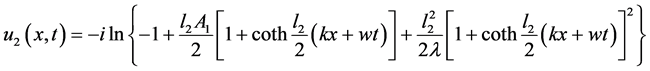 (2.42)
(2.42)
3. 广义变系数KdV-mKdV方程
广义变系数KdV-mKdV方程的形式为
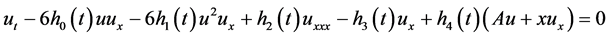 (3.1)
(3.1)
利用齐次平衡原则,平衡(3.1)中的最高阶导数项和最高幂次的非线性项,得 。于是,(3.1)有如下形式的形式解
。于是,(3.1)有如下形式的形式解
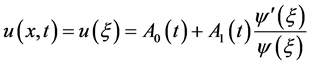 ,
, ,
,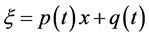 (3.2)
(3.2)
把(3.2)代入(3.1),比较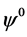 ,
,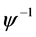 ,
,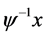 ,
,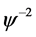 ,
, ,
,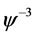 ,
,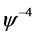 的系数得
的系数得
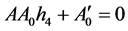 (3.3)
(3.3)
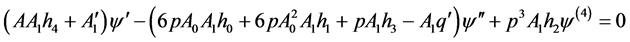 (3.4)
(3.4)
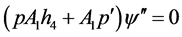 (3.5)
(3.5)
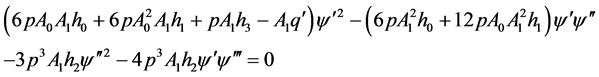 (3.6)
(3.6)
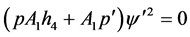 (3.7)
(3.7)
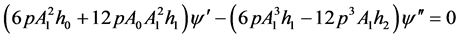 (3.8)
(3.8)
 (3.9)
(3.9)
由(3.3)可得: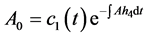 ,由(3.5)和(3.7)可得:
,由(3.5)和(3.7)可得: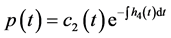
由(3.9)可得: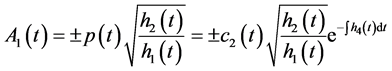
由(3.8)可得:
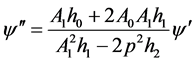 (3.10)
(3.10)
把(3.10)代入(3.6)得到:
 (3.11)
(3.11)
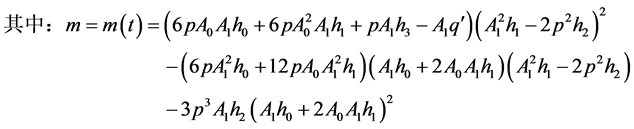

把(3.11)代入(3.4)可得:
 (3.12)
(3.12)
其中: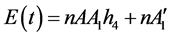 ,
,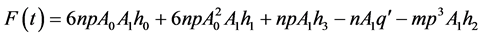
给(3.12)的两端对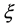 积分两次可得:
积分两次可得:
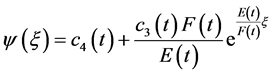 (3.13)
(3.13)
从而:
 (3.14)
(3.14)
于是
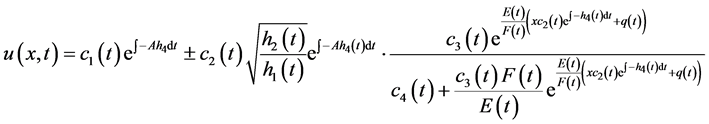 (3.15)
(3.15)
若令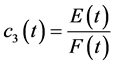 ,
,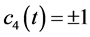 ,得到广义变系数KdV-mKdV方程的精确行波解如下
,得到广义变系数KdV-mKdV方程的精确行波解如下
 (3.16)
(3.16)
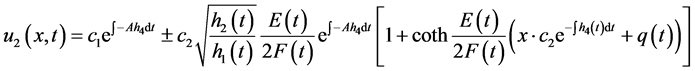 (3.17)
(3.17)
本文把修正的简单方程法推广到求解sine-Gordon方程和变系数方程中,得到sine-Gordon方程和广义变系数KdV-mKdV方程的精确孤波解。鉴于修正的简单方程法是受G'/G展开法的启发产生的一种新方法,因此,如果能够类似于G'/G-展开法的推广将此方法进行推广就有可能给出非线性发展方程的其他类型的精确解。
基金项目
国家自然科学基金资助项目(11261037, 10461006);内蒙古自然科学基金资助项目(2014MS0111);内蒙古师范大学“十百千”人才培养工程资助项目(RCPY-2-2012-K-033);内蒙古师范大学研究生科研创新基金资助项目(CXJJS15073);内蒙古自治区研究生教育创新计划资助项目。