1. 引言
保证国家粮食安全是一项长期的、须臾不可放松的历史重任，粮食关系着国计民生，是一个具有时间和空间永恒性的问题。合理利用与保护耕地资源，增加粮食生产能力，是实现社会经济可持续发展的重要课题。在以往的研究中可知，相同情况下，分层抽样的误差要小于其他概率抽样(简单随机抽样、整群抽样、系统抽样等)。因此本文选取分层抽样的方法，将山西省城市按照南部、中部和北部分为三层。分别利用比估计和回归估计的方法来计算粮食总产量。已知粮食种植面积与粮食总产量有显著的相关关系，所以本文选择粮食种植面积作为辅助变量，进而利用简单估计、比估计和回归估计来预测粮食总产量。
对粮食产量的预测方面，国内学者主要采用了多元线性模型、灰色预测等时间序列方法，如周永生等 [1] 对影响粮食产量的各种因素进行分析，应用多元线性回归分析法建立了广西粮食产量的预测模型。孙东升等 [2] 利用HP滤波法将粮食产量分离为时间趋势序列和波动序列，对趋势序列建立了关于时间t的趋势模型，以及王步祥 [3] 系统评价了国内外有关粮食产量及灰色系统理论研究的状况，回顾了我国粮食生产的历史阶段，深入系统剖析了我国粮食发展的现状，从现有数据及资料出发，分析了我国各大区域及粮食主产区的生产情况。但是利用比估计和回归估计方法研究粮食产量的成果较少，但这种方法存在其合理性和实用性，因此本文从此角度出发，从山西省统计信息网中，得到2013年粮食产量与种植面积数据，利用简单估计、比估计和回归估计的方法来预测粮食产量，并进行精度比较。
2. 理论基础
2.1. 分层抽样
分层抽样又称为类型抽样或分类抽样，即在每一层中独立进行抽样，最后将各层样本组成总的样本，由于总体参数未知，所以利用各层抽样得到的样本对参数进行估计，这种抽样就称为分层抽样。
2.2. 比率估计
实际中我们真正关心的变量Y通常不易获得衡量数据，那么，遇到这种问题通常退而寻找一个与Y有关的变量X，称X为辅助变量，并且X的总体总值需为已知的。在实际抽样调查中，选取辅助变量X通常出于以下几个原因：
1) 同一个变量的前一期调查结果存在着当期与前一期相比变化不会太大的假设，即不会因为该量造成很大的估计误差；
2) 与主要变量之间整体上存在某种比值关系，即隐含着两者比值关系的变化不会太大的假设，即不会因为利用二者的比值而造成很大的估计误差。
比率估计通常分为分别比估计和联合比估计，简而言之，分别比估计就是先“比”后“加权”，而联合比估计就是先“加权”后“比”，具体计算过程如下：
分别比估计，总体均值和总体总量的分别比估计为：
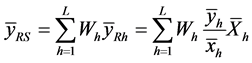
统计量的方差为：
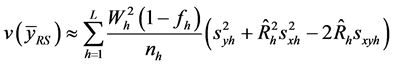
式中，
为层权；
为第
层的抽样比；
分别为第
层指标
的方差以及它们的协方差，
。
联合比估计，总体均值和总体总量的联合比估计为：
式中，
分别为
和
的分层简单估计量；而
。
统计量的方差为：
2.3. 回归估计
当通过分析发现和之间存在近似的线性关系，但不通过和构成的坐标系的原点，也就是所谓截距为非0数，那么这时比率估计就不再适用，违背了其最初的假设，但是两者的线性关系仍为最好的解决问题的入手点，所以利用对的线性回归关系进行估计。
将线性回归估计的思想与分层随机样本的实际情况相结合，类似于比率估计，同样有两个类型，一种是分别回归比估计，主要思想为对每层样本先求回归估计量，然后对各层的回归估计量进行加权平均；另一种是联合回归比估计，方法是对两个变量先分别计算出总体均值或总体总量的分层简单估计量，然后再对它们的分层简单估计量来构造回归估计，具体计算过程如下。
分别回归估计，对于的分别回归估计为：
式中，
为样本回归系数；
对于统计量
的方差为：
式中，
是第
层样本相关系数的平方。
联合回归估计，对于的分别回归估计为：
对于统计量
的方差为：
。 [4]
3. 不同的抽样方式用于粮食产量分析的实证
3.1. 总样本量
总体包括山西省的119个县(县级市，地级市市区)，拟利用其中的11个县(县级市，地级市市区)调查粮食种植面积和粮食产量，因此样本量
。
3.2. 层的划分
按山西省不同地理位置，将总体划分为3个层，分别对应山西省北部地区、山西省中部地区和山西省南部地区。其中北部地区包括大同、朔州、忻州；中部地区包括太原、阳泉、晋中、吕梁、长治；南部地区包括临汾、晋城、运城。
3.3. 各层样本量
采用比例分配原则确定各层样本量，根据层的大小
，
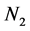和
，在总体样本量的基础上确定各层样本量
。
3.4. 样本抽取
按照随机抽样的准则，利用SPSS软件在各层内随机地抽取县(县级市、地级市市区)进行粮食种植面积和粮食产量的统计，最终入选的11个样本点分别对应为大同市灵丘县、朔州市平鲁县、忻州市忻府区、太原市晋源区、晋中市左权县、吕梁市交城县、长治市长治县、长治市壶关县、临汾市乡宁县、晋城市泽州县以及运城市芮城县。对上述11个样本点进行数据搜集，得表1。其中Xhi代表第h层的第i个样本县(县级市、地级市市区) 的2013年的粮食种植面积，Yhi代表该县(县级市、地级市市区) 2013年粮食产量。
3.5. 数据整理
根据表1中的调查数据，计算得出表2中的相关统计量的值。
3.6. 总体总值估计
基于上述数据整理的结果，采用分层随机抽样的分别比估计、联合比估计、分别回归估计和联合回归估计对总体总值做出估计。
1) 简单估计
，
，
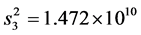
表1. 数据表
表2. 计算结果
2) 分别比估计
所以
3) 联合比估计
所以
所以
4) 分别回归估计
所以
5) 联合回归估计
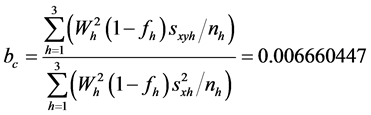
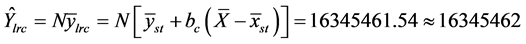
所以
表3. 结果对比
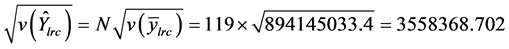
因此，运用五种方法对总体总值进行估计，得到的估计量分别为：简单估计为16,299,884，分别比估计为15,490,970，联合比估计为14,334,300，分别回归估计为13,428,007，联合回归估计为16,345,462。
3.7. 精度比较
对以上五种方法所得的结果总结于表3进行比较。
从表3可以看出，针对本问题来说，有：1) 回归估计的效果均好于比估计和简单估计；2) 对于粮食产量的预测，分别回归估计的误差最小，效果较优。
4. 结论
本文采用分层随机抽样方法抽取了山西省11个样本县(县级市、地级市市区)，然后收集样本区的粮食种植面积，运用统计方法中的简单估计、比估计法和回归估计法对下一年的粮食总产量进行了预测，对总体做出了有效估计。
在本项调查研究中，相较于简单估计和比估计而言，回归估计法的误差更小，估计的精度更高，具有更高的可信度。这为今后基于粮食播种面积调查的样本数据进行总体估计提供了一条新的优化技术路线，即充分利用可以得到的辅助信息，如粮食种植面积，巧妙借助回归估计法，尤其是利用分别回归估计的方法，提高总量估计的精确性和可靠性，如估计粮食总产量。