1. 引言
降水观测值对于气象学、气候学、水文学、地质分析、环境监控都必不可少。降水资料通常是通过已有的雨量站、气象站(包括降水、温度和风速等)收集,因此这些数据都是离散的、局部的和有限的空间点。然而,对于单独的降水站点资料作为径流估计的输入会带来很大的不确定性 [1] [2] 。时空连续的降水资料,需要根据已知降水站点的资料通过空间插值得到。
现有的空间插值方法可以被概括为确定性和地理统计的插值方法 [3] ,地理统计的方法正在广泛的使用。地理统计提供了一种考虑空间变量的插值方法,经常使用变异函数来描述空间变量结构。克里金法提供了一个在有限区域内对空间变量进行无偏最优估计的方法。Borga和Vizzaccaro [4] 用线性函数作为普通克里金插值的变异函数和复二次函数曲面拟合的插值方法进行降水插值比较,发现普通克里金法的插值精度较好。Chen等 [5] 用线性函数作为普通克里金插值的变异函数,比较了普通克里金法、最邻近法、局部多项式法、径向基法、倒距离权重法在中国1951~2005年的日降水插值结果,得出普通克里金法的精度最高。现有关于降水的空间插值研究中,大多数研究倾向于对不同插值方法进行比较,很少涉及到插值方法的参数设置和变异函数的选择。许多研究在应用克里金法时多是根据经验人为的选定一个变异函数,因而缺乏可靠的依据。S.Ly等 [6] 分析了在比利时乌尔特河流域不同变异函数对日降水插值影响,发现最合适的变异函数是高斯函数。Lin和Chen [7] 认为变异函数的计算对于降水插值精度有很大影响,变异函数没有拟合好,克里金法将不会产生最好的插值。因此,变异函数的选择对于克里金插值的方法至关重要。
由于降水具有间断性和空间不连续性,而且日降水零值较多,因此降水的空间插值与其他要素相比具有更大的困难 [8] 。目前,较多研究者考虑的是年降水、月降水尺度下的克里金插值变异函数的比较,张余庆等 [9] 研究了江西多年平均降水量空间插值模型的选取与比较,王常森等 [10] 研究了淮北平原年降水量空间插值模型的比选。日降水的变异函数比较研究较少,但随着分布式水文模型的发展,对日降水插值的要求也越来越高。
本文的目的是得到普通克里金日降水插值适应性较好的变异函数。选取了普通克里金插值常用的4种变异函数,设置变异函数参数后计算得估计值,使用交叉验证的思路,对插值结果使用不同的评判方法,比较分析4种变异函数日降水的插值结果,得到适应性较好的变异函数。
2. 研究方法
2.1. 插值方法
普通克里金法是一种经常使用的地理统计的插值方法,而地理统计是一种既考虑样本值又重视样本空间位置及样本之间相关性的方法,通常使用变异函数作为描述空间相关性的核心。
2.1.1. 变异函数
变异函数用来刻画区域化变量在空间中的相关程度,定义为区域化变量在相距为h的任意两点处的平方均值的一半,其计算公式如下:
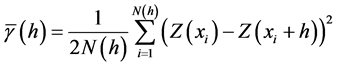 (1)
(1)
式中: 为该点处变异函数的值;
为该点处变异函数的值; 为分离距离为h的采样点对的数目;
为分离距离为h的采样点对的数目; 和
和 为采样间隔为
为采样间隔为 的已知点的降水数据。
的已知点的降水数据。
根据变异函数的特性,选取适当的半变异理论函数,本文选取的半变异理论函数有常用的四个,分别为球面函数、高斯函数、指数函数、线性函数,其公式如下。
球型函数(Spherical function):
 (2)
(2)
高斯函数(Gauss function):
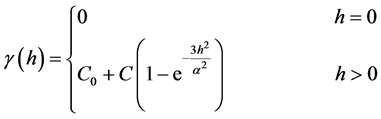 (3)
(3)
指数函数(Exponential function):
 (4)
(4)
线性函数(Linearfunction):
 (5)
(5)
在以上四个函数中, 为分离距离,
为分离距离, 表示块金值,
表示块金值,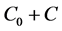 表示基台值,
表示基台值,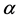 表示变程,即曲线到达基台值时所对应的距离。
表示变程,即曲线到达基台值时所对应的距离。
在选择分离距离 时,要考虑到在大分离距离下的测量资料代表样本采集地边缘的方差结构,而不是样本主流的方差结构,近距离的变异函数值比远距离的变异函数值所起作用更大。因此要将分离距离控制在有意义的研究范围内, 通常应保证分离距离|h| ≤ L/2 [11] ,L是研究区域沿某方向的最大距离。
时,要考虑到在大分离距离下的测量资料代表样本采集地边缘的方差结构,而不是样本主流的方差结构,近距离的变异函数值比远距离的变异函数值所起作用更大。因此要将分离距离控制在有意义的研究范围内, 通常应保证分离距离|h| ≤ L/2 [11] ,L是研究区域沿某方向的最大距离。
受样本数量限制,步长值的选取不宜过小。在每一个分离距离上用来计算样本变异函数的数值一般应大于30个点对 [11] ,点对数太小的变异函数值不可用。因此虽然适当减小步长值一般能提高函数拟合精度,但如果参与计算的数据点对太少,则只能增加步长值。
2.1.2. 普通克里金法
普通克里金(Ordinary Kriging)提供了一个在有限区域内对空间变量进行无偏最优估计的方法,是根据样本空间位置不同、样本间相关程度不同,对每个样品赋予了不同的权,进行滑动加权平均,以估计待测点的值。
 (6)
(6)
式中: 为待测点的估算值;
为待测点的估算值; 为第
为第 个样本点的实测值,
个样本点的实测值, 为参与计算的实测样本个数,
为参与计算的实测样本个数, 为第
为第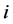 个样本点的权重系数。
个样本点的权重系数。
而权重是根据克里金插值的无偏估计和方差的最小得到。公式如下:
 (7)
(7)
式中: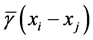 为第
为第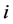 个和第
个和第 个样本点之间的半方差,
个样本点之间的半方差, 为第
为第 个样本点与待插点之间的半方差,这两个量均可以从已拟合的变异函数得到,
个样本点与待插点之间的半方差,这两个量均可以从已拟合的变异函数得到, 为拉格朗日乘子,
为拉格朗日乘子, 为参与计算的实测样本点个数。
为参与计算的实测样本点个数。
2.2. 评判方法
交叉验证
交叉验证法(Cross-validation)通过求出检验站点的实测值与估计值之间的误差,作为评价插值方法效果的依据。
本文选用平均误差ME (Mean Error),用来评估插值方法的无偏性,其值越小越好;平均绝对误差MAE (Mean Absolute Error),表示插值结果存在系统误差的大小,其值越小越好;均方根误差RMSE (Root Mean Squared Error)表示插值结果偏离实际值的大小,其值越小越好。
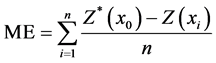 (8)
(8)
 (9)
(9)
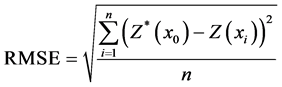 (10)
(10)
式中: 为待插点的估算值;
为待插点的估算值;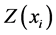 为第
为第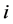 个样本点的实测值,
个样本点的实测值,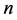 为参与计算的实测样本个数。
为参与计算的实测样本个数。
3. 研究区域及资料
洣水是湘江的一级支流,本文研究的是洣水所在子流域。该子流域位于北纬26˚1'~27˚23',东经112˚57'~114˚6'之间,整个子流域面积是9929 km2。该子流域高程范围从6~2061 m (图1),东南为山地,高程超过1000 m,其余大都为起伏不平的丘陵与沿河平原。东南部山地主要是变质岩,中部西南部主要为红岩和第四纪松散堆积物。该子流域是亚热带季风气候,年均气温在17℃以上,年均降水为1600 mm,东南降水较大,可达1900 mm以上,西南降水较小,在1400 mm左右,降水从东南向西北递减。全年降水多集中于3~7月,汛期(4~9月)降水占全年的70%左右。
本文的降水数据来源于洣水所在子流域及子流域周边一共43个雨量站(图1)。这些站点具备1990~2005年完整的日降水数据,且空间分布比较均匀。以40个雨量站作为计算站点,以悟田洲站、承坪站、打鸟坳站这3个站点作为交叉验证的检验站点。
4. 结果与讨论
4.1. 变异函数参数的选择
在计算变异函数参数时,使用的是洣水所在子流域及周边40个计算站点,其中东江站和清水江站距离最远,为172,561 m,故在进行半方差分析时,选取此距离值的一半(约86,280 m)作为半方差分析的最大步长值。基于以上分析,在对现有数据进行分析时,经过多次步长设置的比较,最终选取步长值为10,785 m,以保证参与计算半方差的点数至少为30,以此获得的步长组数为8。
由于变异函数的使用,克里金插值会产生不好的结果——插值结果小于零。通常,这里有两种方法来避免不好的插值结果:一是通过Deutsh [12] 给出的经验纠正;二是直接将小于零的值替代为零。本文是直接将小于零的值替代为零。

Figure 1. DEM and distribution of rainfall stations in Mishui Basin
图1. 洣水子流域数字高程及站点水系分布图
4.2. 交叉验证结果与分析
在对普通克里金插值结果进行评估时,对于所有站点日降水都为零的日子,我们认为在整个流域都是没有降水的,因此不会对这些日子进行插值。本文已有的16年日降水资料中,无雨的日子有983天。
4.2.1. 相关系数比较
图2给出普通克里金法三个检验站点的4种不同变异函数16年日降水量实测值和估计值结果的对比及其相关系数。从相关系数可以看到,这4种不同变异函数的实测值与估计值均有较高相关性,相关系数在0.8左右。由于所选检验站点的位置不同、所使用插值的已知站点不同,这三个检验站点的相关系数不尽相同,但是对于每一个检验站点的4种不同变异函数相关性的比较,可以看到指数函数的相关性最高,球型函数的相关性次之。其中指数函数和球型函数比较相近,高斯函数和线性函数相关性比较相近。从图中也可以看到,对于每一个检验站点,指数函数和球型函数的估计值在斜率为1的斜线附近较为集中,而高斯函数和线性函数的估计值在斜

Figure 2. The correlation coefficients and comparison of four different variogram functions between estimated and observed value for daily rainfall (a) Exponential function; (b) Spherical function; (c) Gauss function; (d) Linear function
图2. 四种不同变异函数日降水实测值与估计值对比图及其相关系数 (a)指数函数;(b)球型函数;(c)高斯函数;(d)线性函数
率为1的斜线附近较为分散,偏离较大,导致相关系数偏低,可以认为使用高斯函数和线性函数插值出现极值误差的几率较大。
4.2.2. 不同检验指标比较
本文采用平均误差ME、平均绝对误差MAE和均方根误差RMSE 3个指标来衡量4种不同变异函数的插值效果,其结果如表1。从这三个检验站点的ME来看,高斯函数的误差最大,明显高于指数函数、球型函数、线性函数。从MAE和RMSE来看,指数函数的误差值最小,球型函数的误差次之,但是指数函数和球型函数的误差明显的小于高斯函数和线性函数,说明指数函数的估计值误差范围较小,与实际值更为接近,能更好的适应日降水插值。
由于该地区无降水的日子有983天,将会影响到对较大雨量情况的检验结果,因此对降水量大于等于10 mm的情况,也进行了检验,结果如表2。表2中三个检验站点的ME均小于零,说明这4种不同变异函数的估计值相较于实测值系统的偏小,相比于表1的ME,可以得到降水量大的日子普通克里金插值结果具有一定的减小作用。同时,表2的MAE和RMSE相较于表1均明显增大了很多,说明随着降水量的增大,插值的误差范围也会增大。但随着降水量的增大,指数函数和球型函数的误差范围非常接近,指数函数的误差不再是最小的了,但还是明显的低于高斯函数和线性函数。
4.2.3. 不同降水级别的插值准确率比较
以降水量(R) 10,25,50 mm为标准,对大于等于界限的插值结果进行分析。如果实测值大于等于标准值,其插值结果也大于等于标准值,则认为插值准确;如果实测值大于等于标准值,插值结果小于标准值,则认为插值结果不准确。分别统计满足这4种不同变异函数情况下的样本数,然后除以二者的样本数总和,可以得到这4种变异函数所占的比例。
从图3三个检验站点的准确率来看,随着降水量级的增大,指数函数误差最小的优势不再明显,但无论在哪个降水量级,指数函数和球型函数插值结果的准确率非常接近,并且高于高斯函数和线性函数。随着降水量级的增大,插值的准确率有明显较小的趋势。在R ≥ 10 mm (中雨)时,这三个检验站点的准确率在80%左右;在R ≥ 25 mm (大雨)时,准确率在70%左右;在R ≥ 50 mm (暴雨)时,准确率在60%左右。由此可见,在降水量较大的情况,尤其是对暴雨的插值,普通克里金插值的方法不是很好。

Table 1. The cross-validation results of four different variogram functions between estimated and observed value
表1. 4种不同变异函数交叉验证检验站点结果

Table 2. The cross-validation results of four different functions between estimated and observed values (daily rainfall ≥ 10 mm)
表2. 四种不同变异函数交叉验证检验站点结果(日降水量 ≥ 10 mm)


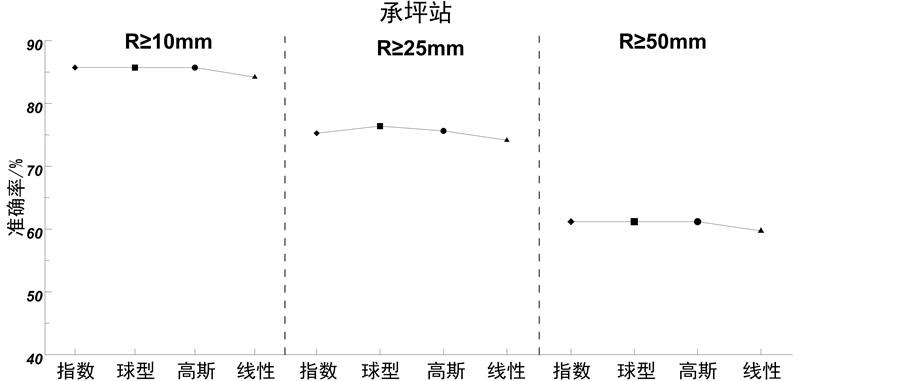
Figure 3. Accuracy of different precipitation grade of four different variogram functions
图3. 四种不同变异函数在不同降水级别下的准确率
5. 结论
本文研究了普通克里金法在4种不同变异函数的情况下,对湘江洣水子流域40个雨量站的日降水资料插值,设置变异函数步长值为10,785 m,步长组数为8,从相关系数、检验指标、不同降水级别准确率这三个方面对交叉验证的3个检验站点的插值结果进行比较分析,得出以下结论:
1) 指数和球型函数对于普通克里金日降水插值的适应性较好。指数函数在日降水量级较小时适应性更好;在日降水量级增大时,指数和球型函数对普通克里金插值的适应性均较好。
2) 普通克里金法的插值结果在降水量大的日子普遍偏小。
3) 随着降水量级的增大,日降水的误差明显增大。
基金项目
国家自然科学基金重点项目(51539009)。