1. 前言
在常见的PCB板的电子元件中，大多数的电子元件外形无非是矩形、圆形两种。如果能在检测中，准确快速的对这两种外形的元件的外轮廓进行定位，将极大程度的提高企业生产线上对其识别的准确性和稳定性。在PCB定位中，如果预知每个圆形元件的坐标区域，在实际匹配计算时，只需适当扩大搜索区域，在该区域内即可找到一个最大的最佳匹配圆即可。
在图像处理中，Hough圆定位算法是Paul Hough在1962年提出的一种图像边缘检测技术，它可以检测图像空间中的任意解析曲线 [1] 。目前很多已有的圆定位算法，大都是基于Hough算法的改进。目前Hough圆定位算法会在一张图中会计算得到多个符合条件的圆，而非在区域内优选出单一的圆，因此，无法满足PCB定位中圆定位算法的目的，在一个区域内找到一个最优圆的需求。
基于模板匹配的圆定位算法在实际中也有使用，该方法可以在一个区域中找到和模板匹配最佳的圆，但是该方法，无法用同一个圆模板，满足不同半径的圆的定位。PCB定位中圆的直径，可能会由于拍摄相机的位置变化而有改变，这是模板匹配的算法所无法满足的。
目前PCB电路圆的定位，有基于Hough变换 [2] [3] [4] 、基于势函数 [5] 等方法，但是都没有很好的解决在设定区域内快速定位最大半径圆的问题。
本文设计了一套基于边沿梯度方向统计的圆定位算法，在确定的图像内找到最大的匹配圆，首先使用Canny边缘检测结合Sobel变换先计算得到圆心区域的大概位置，然后统计对圆心区域有贡献的点，得到目标圆的圆周上的点，然后再以得到的圆周，对圆心进行二次定位，从而得到最终的圆心和半径。实验表明对于边沿清晰的目标圆，该算法速度较快，长宽200像素内的图像，运算速度在50 ms以内。对于圆形的电子元件允许一定程度的圆周不完整(大于70%周长)，允许一定程度的圆周变形(椭圆)，对圆的半径变化也有一定是适应性。该算法于灰度图像进行计算，所以对于彩色、灰度CCD相机都可满足，对于边沿清晰的圆形物体识别准确度高。
2. PCB板的圆定位算法
图1给出了圆定位算法，其主要包含四个主要处理过程：预处理、圆心粗定位、半径计算、圆心再定位。
图1所示的圆定位算法流程图中虚框框起来的是四个主要处理工作，接下来以最常见的电容元件为例，介绍论文提出的定位算法的这四个具体处理工作。介绍每一处理工作的内容、处理的结果，以及得到的结果。
2.1. 预处理
2.1.1. 灰度化
本步工作主要完成对所拍摄的彩图进行灰度化转换。方法是基于计算公式1把输入的彩色图像(图2左所示)的每一坐标值对应计算，从而使其转换为单通道的灰度图像(如图2中所示)，即将RGB三通道彩色图像通过变换，转化为灰度图像的计算。
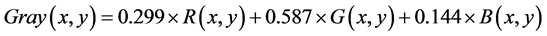(公式1)
其中x，y为图中每个点的坐标值。
2.1.2. 高斯平滑处理
对于图像非圆周的细节信息，并不会对圆定位有所贡献，反而会对定位工作带来干扰，所以要减弱这种干扰。
本文采用高斯平滑算法 [6] [7] ，用它来减少图像噪音以及降低细节层次，平滑窗口取5 × 5像素。图2右显示出图像的细节已被模糊处理。
2.2. 粗定位圆心区域
粗定位圆心区域的工作可分为：计算边沿、计算边沿点Sobel切线、生成交点图和计算滑动窗口圆心四个步骤，从而得到一个圆心的圆区域。
2.2.1. 边沿的计算
边沿(边缘)：图像的边缘是指图像局部区域亮度变化显著的部分，该区域的灰度梯度变化一般可以看作是一个阶跃，既从一个灰度值在很小的缓冲区域内急剧变化到另一个灰度相差较大的灰度值。通常图像的边沿集中了图像的很多信息，是图像场景识别和理解的基础，是图像分割、定位、测量、识别的重要手段。图3给出了边沿方向和梯度方向，图中高度表示灰度值。
圆心在圆定位的过程中是通过圆周的定位来确定的，圆周在图像中即为的圆的边沿。本文对此采用最常用的Canny算法来计算圆的边沿图，得到图4所示结果。Canny边缘检测算子是John F. Canny [8]
Figure 2. Gray and smooth processing of color image
图2. 彩色图的灰度化和平滑处理
Figure 4. Based on the edge of Canny computing
图4. 基于Canny计算边沿
于1986年开发出来的一个多级边缘检测算法，主要包括五个处理步骤：
1) 应用高斯滤波来平滑图像去除噪声；
2) 找寻图像的强度梯度(intensity gradients)，用一阶偏导(Sobel算子)计算梯度的方向和幅度值；
3) 应用非最大抑制(non-maximum suppression)技术来消除边误检；
4) 应用双阈值的方法来决定可能的边界；
5) 利用滞后技术来跟踪边界。
2.2.2. 边沿点Sobel切线方向的计算
Sobel [9] [10] [11] 算子常用于边缘检测中计算图像亮度函数的一阶梯度之近似值。在图像的任何一点使用此算子，将会产生该点对应的梯度矢量或是其法矢量。本文使用的Sobel算子如下：
Sobel X: X方向求导，将图像(I)与一个奇数大小的内核进行卷积。
Sobel Y: Y方向求导，将图像(I)与一个奇数大小的内核进行卷积。
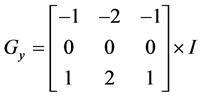
对灰度图的每一个点分别计算Sobel X Y卷积得到X、Y两个方向的Sobel图得到图5所示结果。
从图5左和中图中可看出X，Y方向的Sobel计算结果即为X、Y方向的灰度变换梯度，将其视为该
点的正弦、余弦，那么过该点的正切即为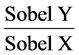
。
由于本文只对图像的边沿感兴趣，所以只需要计算Canny边沿图上的每一个边沿点的正切线即可。
以边沿图中边沿点(56,56)为例，Sobel X的(56,56)值为s_x = 573，Sobel Y的(56,56)值为s_y = 653，
(56,56)点的正切值为，(i,j)为计算点的坐标，计算得到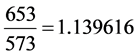
，计算反正切，得到角度为θ = 48.73˚，
从图6右中看到计算和实际方向一致。
2.2.3. 绘制交点图
对Canny的边沿图(图4)中白色的边沿上的每一个点，计算正切值，并将计算后得到的切线绘制到统计图中，最终得到对应的图6所示的切线交点图，处理步骤如下：
1) 创建空白的切线交点图Cross；
2) Canny图中按坐标顺序，取一点边沿点C；
3) 根据SobelX，Sobel计算C点的正切；
4) 在Corss图中，绘制经过C的切线；
5) 如果切线经过点P，P当前的值位D；
6) 修改P点的值为D + 1；
7) 依次计算切线上每一个点的新值；
8) 计算Canny图中下一个边沿点，直到遍历完毕。
2.2.4. 滑动窗口圆心区域粗定位
在图6右中可看出，亮度最高的区域就是边沿切线交汇最多的区域，即圆心所在的区域。粗定位步骤如下：
1) 图的宽W，高H，设定滑动窗口的宽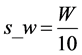为
，高为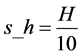
；
2) 设定搜索步长X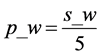方向为
，Y方向为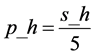
；
3) 遍历全图(图6右)，找到滑动窗口像素和最大的区域，得到粗定位的圆心区域；
Figure 5. Calculation of X Sobel and Y Sobel and its tangent direction diagram
图5. 计算Sobel X和Sobel Y及其切线方向示意图
4) 初始化滑动窗口像素和最大值 sum_max = 0，最大值坐标位置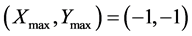
；
5) 滑动窗口左上角坐标
从图7左上角
开始，计算
，区域的像素值总数sum，如果sum > sum_max：
a) sum_max = sum，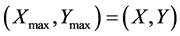
；
b) 更新
坐标为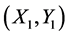
，计算新坐标
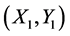的sum，直到遍历完毕；
c)
，
；
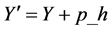d) 如果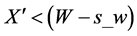
，新坐标为
；
e) 如果
且
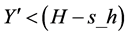，新坐标为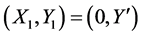
；
f) 如果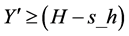
，遍历完毕，结束运算。
通过上面的步骤，得到图7中绿框所示的圆心区域，取绿色矩形的中心点为粗定位圆心Center。
2.3. 半径计算
计算得到粗定位圆心后，再对边沿点集中的点进行筛选，步骤如下：
1) 计算Canny图(图4)的边沿点中，对圆心区域(图8)有贡献的边沿点。
a) 对Canny中每一个白点；
b) 取Canny中白点P(X,Y)；
c) P点切线穿过圆心粗定位区域(图8的绿色区域)；
d) P点到矩形中心的连线，和P点切线的角度小于设定值15˚；
e) P点满足条件则保留，否则删除，最终得到有贡献的边沿图，如图8所示。
2) 以粗定位圆心Center(X,Y)为中心，从外向内确定半径R。
a) 图像宽高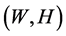
。X，(W-X)，Y，(H-Y)四个值中最小值，作为搜索半径的最大值
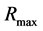，半径的搜索区域为
，
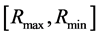，搜索宽度为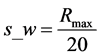
；
b) 初始
，计算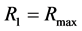
，
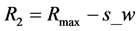，环形区域内的所有白点数目Sum；
c) 如果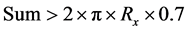
，即环形区域达到70%的圆半径，则得到最终的半径R；
d) 否则
，继续搜索，直到找到。如果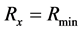
，还未找到，则定位半径失败。
最终计算得到的半径R如图9所示。
2.4. 圆心再定位
粗定位的圆心并不准确，在计算得到半径后，我们还需要对圆心再一次定位，步骤如下。
1) 将图9中，半径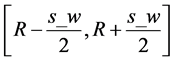
，圆环区域内的边沿点保留，去掉其他的边沿点。
2) 如图10中白色边沿所示。
3) 根据SobelX、SobelY，对图10中每个边沿点，按照圆心粗定位的算法，得到切线交汇图(图11)。
4) 在切线交汇图中，使用圆心滑动窗口(半径为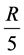
)，找到切线交汇最多的区域，小圆圆心即为最终的圆心，如图10中心点所示。
最终，获得圆定位结果如图12所示。
2.5. 算法验证
本文算法在电子电路检测中，主要针对的圆形检测对象可以是：电容、蜂鸣器、锂电池等圆形手插件、板卡上的各种孔、洞、定位点、螺丝等各种紧固件，以及其他圆形边缘元件。为验证本文算法的准确性和实际性能，首先要对相应的电路板进行拍照，应用本文提出的圆定位算法对其上面的圆形元件或板卡上的孔洞进行检测实验。
为此，本文搭建了包括拍摄平台、算法平台、识别程序三部分组成的测试环境。其中：拍摄实验平台是由千万像素CCD工业相机、镜头、LED光源、封闭机柜、工控机组成；算法测试平台是在高性能PC (intel i5 CPU、4G DDR3 1600内存、运行Win7操作系统)运行；识别程序是使用VS2005的MFC编写，图像库使用OpenCV2.0。选择了几种典型的圆形元件，如：电容，螺丝，圆形打孔，塑料、金属支撑立柱等常见的圆形元件。实验结果如表1所示。
采用圆定位算法得到的圆心平均偏移误差在2个像素以内，半径误差在4个像素之内，运算时间和图像的像素数目有关，对于200 × 200像素的图像，运算时间在30 ms左右，可以满足大多数圆形元件的准实时定位需求。与传统的基于Hough变换的圆定位算法相比，该算法数学模型清晰、易于实现、更适用于PCB光学检测系统的定位需求。
表1. 实验结果
2.6. 结论
本文提出的圆形电池定位算法具有一定的通用性，实际应用时，可根据实际需要调节模、canny变换、滑动窗口、圆周比例等参数。如果效果不理想，还可以对模糊、圆心定位、半径搜索的算法加以改进，即可得到满意的效果。
基金项目
天津市支撑项目(15ZXHLGX00380)；天津市支撑项目(15ZXHLGX00360)。