1. 引言
固体氧化物电池储能系统是基于固体氧化物燃料电池(Solid Oxide Fuel Cell, SOFC)和电解池(Solid Oxide Electrolysis Cell, SOEC)两个模式进行电能存储的一个可逆的系统。固体氧化物电池储能系统本质上是一个可逆固体氧化物电池堆,包括两个相互可逆的电化学过程,即将化学能转化为电能的燃料电池过程和将电能转化为化学能的电解池过程 [1] [2] [3] [4] 。当固体氧化物电池储能系统以燃料电池模式运行时,是将燃料转化为电能,也就是发电的过程,即电能的利用;而当固体氧化物电池储能系统以电解池模式运行时,则是将电能转化为燃料能源进行能源存储,也就是电能存储的过程。固体氧化物电池储能系统具有以下突出优点,包括全固态、效率高、成本低和体积小,作为清洁能源展现出良好的商业化前景。
虽然固体氧化物电池系统经过热电联供技术可与涡轮机共同使用,有效利用高温废热,可以使得系统能量效率大于70%,而对于一个可逆固体氧化物电池储能系统来说,电能在该可逆系统内部的循环效率则是评价电能可逆存储的关键技术指标之一。当前,满足商业化大规模批量化生产要求的电能循环效率的技术指标是国际公认的80%。通过系统的热能管理,充分利用系统的热能,可以在一定程度上调节系统操作温度,因此系统的热能管理对于提高系统电能循环效率极为重要。热能管理可以有效提高循环效率,但同时可逆高温热能存储与释放本身就是一个复杂的技术,它涉及了加热和冷却过程中的电能存储、产生与利用,也是一项非常复杂的系统工程。通过可逆固体氧化物电池储能系统可进行高效的电能存储和利用,但是由于操作温度较高容易造成热能损失,因此进行有效的热能管理和利用可有效提高系统的电能循环效率,以达到80%的商业化大规模批量化生产要求标准 [5] [6] 。
由于热能的利用和存储都具有时间性和空间性,为了合理的利用能源并提高能源的利用率,把一段时期内暂时不用的多余的热能存储起来,并在使用高峰时期再提取出来使用,这种方法通常称之为热能的存储与利用。而对于中低温热能的存储技术,当前已发展出多种成熟的商业化技术,例如蓄热锅炉、压缩空气、高温热水等热能存储技术。而随着太空技术和航空技术的发展,又进一步发展出相变材料进行热能存储的新方法,并率先应用于阿波罗十五号飞船。例如,在该技术中,他们将石蜡用于存储在飞行中产生的热,可移动的绝热装置在两次飞行间隙中被打开,储存的热能通过辐射方式散向空间。随着高温热能的温度逐步提高,通过利用相变金属存储热能是高温热能存储的可行途径,而相变金属较大的热容也可实现较大规模的热能存储 [7] [8] [9] 。在一个特定的环境下,当相变金属从固相向液相转变中的热能释放或由液相到固相的相变中的热能存储,可以满足快、高效和大规模的要求。在相变温度的金属相变过程可以有效存储和释放热能,而且可逆相变的特点也让相变金属储能具有可以反复利用的优势。更为重要的是,通过选择不同相变金属,可以将系统的操作温度扩展至高达1000℃的高温。金属的热导率比常规的陶瓷和气体等都大很多,这个特点决定了热能在系统和相变金属之间的传输是高效的。这些优势让相变金属塔或器具可以作为固体氧化物电池堆的先进的热能储存系统。金属铜或银,由于其具有较高的热容,也是常见的热能存储金属材料,可以有效地整合进入可逆固体氧化物电池储能系统作为热能管理的平台。
本文针对高温电池系统热能产生与损失的特点,针对性地提出基于相变金属进行高温热能存储与利用的方法和技术,针对高温电池系统工作特点,设计并构筑了热能存储装置和模型。并结合固体氧化物储能系统构筑了储能电池和热能存储利用这个综合系统,研究系统的能量转化过程及电能循环效率。
2. 固体氧化物电池储能系统建模
2.1. 模型建立
单体电池采用Ni-YSZ燃料电极支撑构型的平板构型,其中YSZ为厚度为10微米的电解质薄膜,而燃料电极支撑体的厚度为2毫米,空气电极厚度为50微米,空气电极集流体厚度为30微米,而燃料电极集流体则采用Ni网。如图1所示,单电池构型尺寸设计为边长为10厘米的正方形构型,通过单体电池的并联形成电池堆,用以实现电能的可逆存储 [10] [11] 。
基于固体氧化物电池储能系统的燃料电池和电解池的电压的计算则是通过计算标准电动势与考虑温度等影响因素对其影响程度之差所得。电池系统的开路电压则是通过燃料电池和电解池两个模式的电化学反应计算所得,两个反应如下。
燃料电池模式:
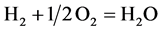 (1)
(1)
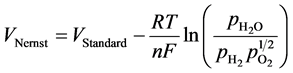 (2)
(2)
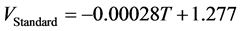 (3)
(3)
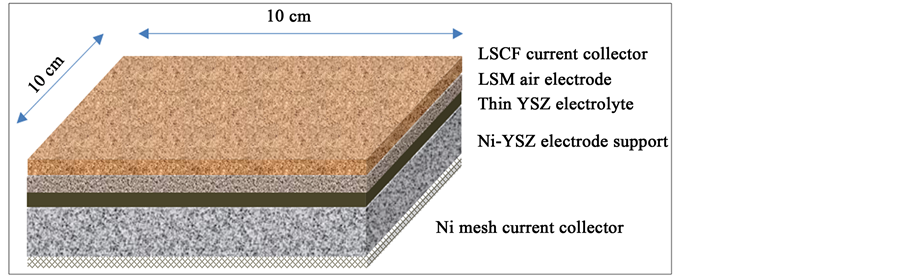
Figure 1. Schematic of the single solid oxide cell with related parameters
图1. 单体固体氧化物电池的构型及相关尺寸
电解池模式:
 (4)
(4)
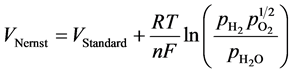 (5)
(5)
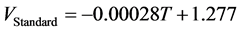 (6)
(6)
由公式可以看到,电池的开路电压依赖于燃料电极和空气电极两侧的反应物的浓度以及在该温度下的标准电动势。因此,如果要增加开路电压,可以通过增加标准电极电势、降低系统操作温度或者改变两个电极的反应物浓度及压力所得。
2.2. 模型计算
为了计算电池各部件在不同温度下的电阻数值,本文采用有关空气电极、燃料电极、电解质和连接体等部件的电阻率用以计算各部件在不同温度下的电阻数值。为更为准确获取各个部件电阻数值,本文采用相关模型进行计算。
2.2.1. 系统部件电阻
对于空气电极,首先计算其电阻率在不同温度下的数值,如公式(7)所示 [12] ,其中T为实际操作温度。
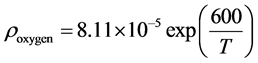 (7)
(7)
而对于燃料电极,其电阻率在上述文献中已有报道,其计算方法如公式(8)所示,其中T是燃料电极的实际操作温度。
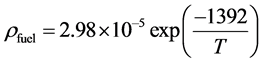 (8)
(8)
而对于YSZ电解质、金属支撑体和连接材料的电阻率的计算方法及公式分别阐述如下:
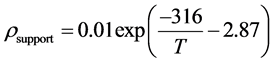 (9)
(9)
 (10)
(10)
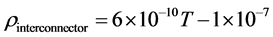 (11)
(11)
2.2.2. 电池总电阻
由上述公式可以得到不同温度下不同部件的电阻率,但是其电阻仍需要考虑作用面积及厚度等参数,计算方式如下:
 (12)
(12)
其中Ri代表对应部件的电阻,ρi代表对应部件的电阻率,li和Ai则分别代表了对应部件的电流通过的长度和面积。
因此,对应于单个固体氧化物电池的电阻则可计算为:
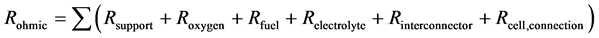 (13)
(13)
其中Rsupport为支撑体电阻,Roxygen为空气电极电阻,Rfuel为燃料电极电阻,Relectrolyte为电解质电阻,Rinterconnector为连接材料电阻,Rcell,connection为接触电阻。
2.2.3. 活化极化电阻
在本文固体氧化物电池储能系统运行过程中,首先遇到的即是活化极化导致的电压降。本文中采用动态的无限体积的燃料电池模型进行模拟计算活化极化电阻 [13] 。基于Bulter-Volmer方程,可以准确地模拟计算出活化极化电阻。公式(14)适合于燃料电池和电解池两种模式:
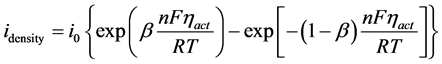 (14)
(14)
在上述方程中,β是电子交换系数,idensity是电极的电流密度,而i0则是代表了交换电流密度,ηact则是代表了活化极化电压。在本方程中,n是参与反应的电子,其数目定为2,F和R则分别是法拉第常数和通用气体常数。而通过本方程尚难以直接计算出活化极化电阻,因此需要对方程进行简化处理并直接计算活化极化电阻。
在较低或较高的电流密度下,Bulter-Volmer方程则可以近似处理为线性方程如下所示 [14] [15] ,公式(15)为较低电流下近似,公式(16)为较高电流下近似:
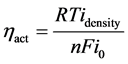 (15)
(15)
 (16)
(16)
2.2.4. 浓差极化电阻
本文将空气电极和燃料电极的浓差极化电阻分别进行了模拟与计算,以便于研究两个电极在固体氧化物电池储能系统中的贡献比例关系。在模拟过程中,采用的计算方程完全适应于燃料电池和电解池两种模式,因为两个模式下的物质扩散基本相同只是方向不同。
首先对燃料电极浓差极化进行计算。在燃料电极一侧,其气氛是氢气和水蒸气的混合气气氛,这对于模拟计算带来了一定的难度。因此本文采取两步进行,首先即是分子扩散过程,即气体分子沿着浓差方向从气相直接扩散至电极表面;而第二步就是气体分子沿着电极多孔结构从电极表面向反应位置的互扩散。
为了计算氢气和水蒸气在电极/电解质界面的浓度,本文采用Fick定律来进行计算 [16] [17] [18] 。虽然采用Fick定律进行计算,但是需进行适当的近似。如下所示,公式(17)给出了氢气扩散通量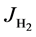 的计算方法:
的计算方法:
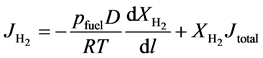 (17)
(17)
其中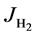 表示氢气的扩散通量,单位是m−2∙s−1;D表示质量扩散系数,单位是m−2∙s−1;l则代表电池边长,单位为m;Jtotal代表氢气和水蒸气的总的扩散通量,但是其总量通常为0,因为氢气的产生和水蒸气的消耗是等量的。
表示氢气的扩散通量,单位是m−2∙s−1;D表示质量扩散系数,单位是m−2∙s−1;l则代表电池边长,单位为m;Jtotal代表氢气和水蒸气的总的扩散通量,但是其总量通常为0,因为氢气的产生和水蒸气的消耗是等量的。
如前所述,还需要考虑气体从电极表面向电解质界面扩散动力学。氢气和水蒸气的扩散系数通常可以采用公式(18)和公式(19)来计算:
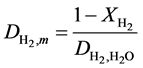 (18)
(18)
 (19)
(19)
其中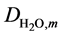 和
和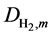 代表了水蒸气和氢气的平均扩散系数,而
代表了水蒸气和氢气的平均扩散系数,而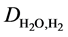 和
和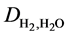 则分别代表两种气体的互扩散系数,其计算方法可参考文献 [19] [20] 。
则分别代表两种气体的互扩散系数,其计算方法可参考文献 [19] [20] 。
而燃料电极总的浓差极化电阻则可表示为:
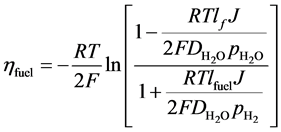 (20)
(20)
上述方程中, 是水蒸气的有效扩散系数,μ则是气体的动态粘度,其计算已有文献进行报道。
是水蒸气的有效扩散系数,μ则是气体的动态粘度,其计算已有文献进行报道。
同理可以计算得到空气电极浓差极化电阻:
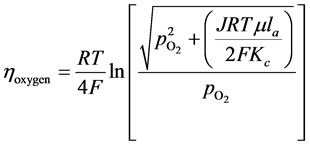 (21)
(21)
2.2.5. 系统电压损失
固体氧化物电池的电压损失包括欧姆电压降和极化电压降两个部分。通常来说,欧姆电压降是由于电池每个部件的电阻导致,这个部分是符合欧姆定律的,可以通过如下公式进行计算:
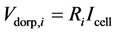 (22)
(22)
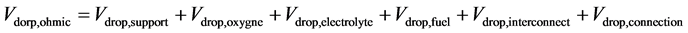 (23)
(23)
2.2.6. 电池系统电压
本文中固体氧化物电池的总的电压降容易通过实验方法进行测试,而分别对应于每个部分的所产生的电压降是不容易测试的。因此,通过分别计算可以直接得到每个电池部件导致的欧姆电压降。而在这个计算过程中,本文需要进行适当的假设,那就是通过每个部件的电流大小是一致的。因此,固体氧化物电池储能系统在燃料电池和电解池模式下的电压则可分别用公式(24)和公式(25)计算如下:
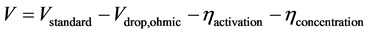 (24)
(24)
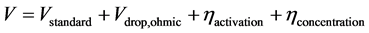 (25)
(25)
3. 平板固体氧化物电池储能系统热能仿真
固体氧化物电池储能系统的热能管理是一项非常复杂的系统工程,系统的热能也受到诸多因素的影响,如果在建模过程中不可能考虑到系统的所有影响因素,这样会使得模型的计算过程非常繁琐而且没有必要,因此本文在建模过程中可以对系统影响较小的因素进行简化与近似。在本文中,为了能够系统地研究固体氧化物电池储能系统的热能管理,本文建立了一个简化的模型计算系统热能的产生和消耗。因此需要作出几个适当的假设:(1) 系统中没有气体泄漏,因此不存在气体热能损失和燃烧产生的热能;(2) 系统的温度是均一的,而在此系统中由于系统温度变化导致的热能的产生与消耗是同步的;(3) 系统外部是绝热的,但是系统材料的热能会导致热能损失并且可以通过热导率进行计算。
在系统中的热能产生与消耗包括电化学热、欧姆热、热能损失及相变金属热存储与释放等,以下本文将逐个计算各种热能,最后再统筹计算整个系统的热能。
3.1. 电化学热
电化学热是由于电化学反应所产生或消耗的热能,其大小可以通过电流大小来计算。系统总的电化学反应所涉及的电量是可以通过电流和时间进行计算,即为:
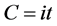 (26)
(26)
其中i为系统的电流大小,而t则是系统运行时间。在固体氧化物燃料电池或电解池模式运行时,所产生的电量C即可以直接转化为氢燃料的产生与消耗的量:
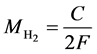 (27)
(27)
其中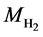 表示氢气的摩尔数,因此可以通过氢气的量计算热能的产生和消耗的量:
表示氢气的摩尔数,因此可以通过氢气的量计算热能的产生和消耗的量:
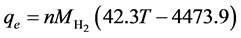 (28)
(28)
其中n为系统中的单电池数量,而T则是系统的操作温度。
3.2. 欧姆热
欧姆热即系统的电阻导致的热能损失,欧姆热无论在燃料电池还是电解池模式下都会产生,其计算符合欧姆定律:
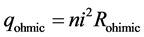 (29)
(29)
其中n为电池数目而i则是通过电池的电流大小,Rohmic是电池内阻。
3.3. 系统热能损失
系统向环境的热能损失也是需要考虑的一个因素。本文从计算系统的外围体积入手,即假设系统处于密闭立方体中。假设立方体容积为V,其表面积Av,即是边长l平方的6倍,通过其导热系数可以计算出热量损失。但是,热损失计算必须确定密闭系统的内外温差,假设系统实际温度为T,而环境温度为Tc,那么根据已有文献报道 [21] 即可计算其热能损失的量:
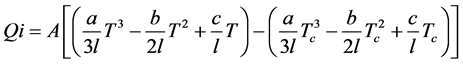 (30)
(30)
3.4. 相变金属热能存储与释放
本文将固体氧化物储能电池系统与相变金属热能管理系统进行整合成为一个一体化的系统,如图2所示,同时向环境的热能损失也是需要考虑的一个因素。本文从计算系统的外围体积,即假设系统处于密闭立方体中。假设立方体容积为V,其表面积Av即是边长l平方的6倍,通过其导热系数可以计算出热量损失。但是,热损失计算必须确定密闭系统的内外温差,假设系统实际温度为T而环境温度为Tc,那么根据已有文献报道 [21] 即可计算其热能损失的量:
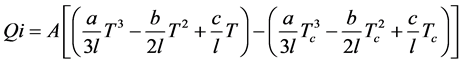 (31)
(31)
而通过相变金属进行存储热能,也需要考虑系统本身的热容,即材料本身和气体的热容导致的热能存储和系统温度变化。在本系统中,由于陶瓷电池体积小,为进一步减小体系的复杂性先将陶瓷材料导致热存储忽略。本文采用金属Ag和金属Cu-Zn合金作为相变储能金属,例如Cu-Zn合金融化温度为
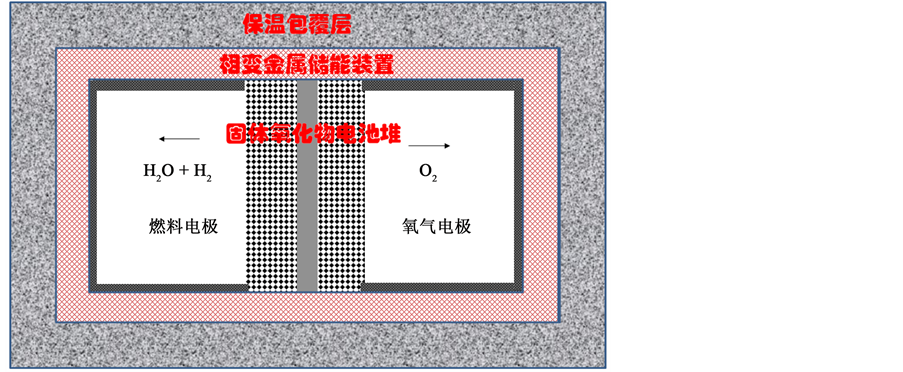
Figure 2. The schematic of heat energy storage system with solid oxide fuel cells
图2. 相变金属热能管理系统与固体氧化物电池的配置示意图
1010℃,因而系统能够达到的最高温度也是1010℃,而高于这个温度系统温度即继续升高耳导致相关部件的损坏 [22] [23] 。因此,本文设计系统的起始和终止温度分别为800℃和1010℃。而金属质量暂定为500公斤,其热容为:
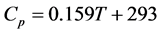 (32)
(32)
为了能够系统地研究固体氧化物电池储能系统的热能管理,本文研究了一个简化的模型进行计算系统热能的产生和消耗。因此需要作出几个适当的假设:
(1) 系统中没有气体泄漏,因此不存在气体热能损失和燃烧产生的热能。
(2) 系统的温度是均一的,而在此系统中由于系统温度变化导致的热能的产生与消耗也就是同步的。
(3) 系统外部是绝热的但是系统材料的热导会导致热能损失并且可以通过热导率进行计算。在系统中的热能产生与消耗包括电化学热、欧姆热、热能损失及相变金属热存储与释放等。电化学热是由于电化学反应所产生或消耗的热能,其大小可以通过电流大小来计算。
4. 结果与讨论
4.1. 平板固体氧化物电池储能系统能量转换影响因素分析
4.1.1. 荷电状态
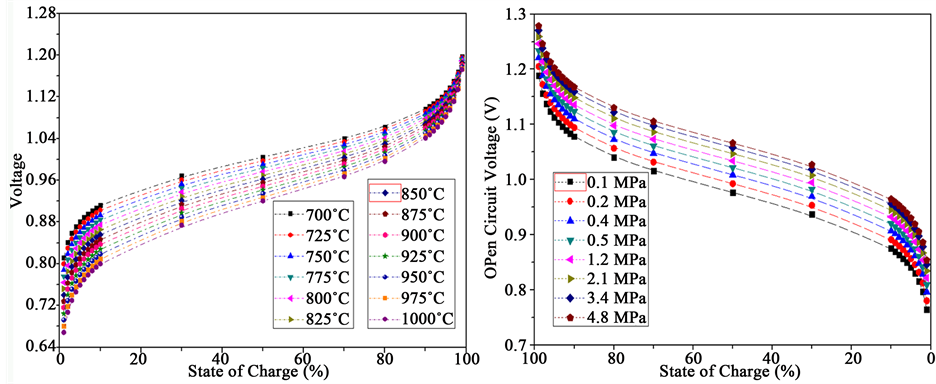
如图3所示,固体氧化物电池储能系统的燃料电极一侧为1%~99% H2/H2O,而空气电极一侧则是暴露在空气气氛中,可以看到荷电状态在同一温度下对系统的开路电压影响剧烈,增加系统荷电状态有助于提高系统的开路电压。
如公式(6)所示,系统操作温度的提高也会降低系统的开路电压,因此本文中,如图3(a)所示,开路电压在较低的荷电状态受到温度的影响较为剧烈,温度降低可显著提高开路电压。但是,通过增加系统压力也可以同步增加开路电压。如图3(b)所示,在相同的荷电状态下增加系统的操作压力,能够明显增加开路电压,其增加幅度在变化50倍压力情况下可达到0.1 V。因此,相对于荷电状态的影响程度,通过压力改变系统开路电压显得更为困难。
4.1.2. 电池部件电阻
如图4所示,固体氧化物电池储能系统的各部件的欧姆电阻,其数值计算是通过考察部件尺寸和
 (a) (b)
(a) (b)
Figure 3. The open circuit voltage of solid oxide cell versus state of charge; (a) versus system operation temperature and (b) versus system pressure at 800˚C
图3. (a) 固体氧化物电池储能系统的开路电压与荷电状态和操作温度的关系,其中系统压力默认为标准大气压;(b) 固体氧化物电池储能系统的开路电压与操作压力的关系,其中操作温度为800℃

Figure 4. The ohimic resistance of each component in solid oxide cell system
图4. 固体氧化物电池相关部件在不同温度下的欧姆电阻
电阻率得到的。可以明显地看到,电解质电阻仍然是电池系统的欧姆电阻的主要来源,虽然本工作中,电解质厚度已为10微米级别,但是其电导率较低仍然导致了较大的电池内阻,相对于电池其他部件,电解质电阻是高出了1~3个数量级。相对于电解质部件,其他部件的电阻则可以忽略不计,仅为电解质电阻的十个或几个百分点。
因此,提高固体氧化物电池储能系统性能的关键手段之一即是降低电解质部件的欧姆电阻。虽然操作温度的提高可以提高相关部件电导率如空气电极和电解质等,但是由计算结果可以看到,在较大的温度范围内,固体氧化物电池部件的电阻并没有大幅度变化。因此,在700℃以上温度范围继续提高温度降低固体氧化物电池内阻的效果并不明显。
4.1.3. 活化极化
如图5所示,固体氧化物电池储能系统运行中其工作过程的本质即是燃料电极和空气电极发生氧化或还原反应进行电化学储能和产生电能,因此电极的活化极化通常是系统效率降低的主要因素。本文采用经典材料构筑的固体氧化物电池储能系统,也不可避免地遇到活化极化较大的问题。
从图5中可以看出,固体氧化物电池储能系统的燃料电极和空气电极活化极化的对比关系。图中所示数据是以800℃操作温度和常压的5% H2/H2O燃料进行仿真模拟。研究发现,无论在燃料电池模式还是电解池模式,活化极化对电流依赖较大。活化极化电势在较低电流条件下较大,即随着电流上升速度较快,这说明两个电极在启动时需充分活化。而随着电流进一步增加,其活化过电势增加缓慢,因为较大的电流有助于活化电极从而减小了活化过电势的增长速度。针对于两个电极活化过电势的差异,可以明显看到燃料电极比空气电极的活化电动势要小一倍多,这说明燃料电极活性提高仍然是制约固体氧化物电池储能系统性能提高的关键因素之一。
4.1.4. 欧姆极化
相对于非线性的活化极化来说,欧姆极化对应于固体氧化物电池储能系统的欧姆电阻在系统运行过程中导致的电压降,并符合欧姆定律。因此,欧姆极化是属于线性的极化,其大小应依赖于电流的大小。如图6所示,符合欧姆定律的欧姆极化随着电流是线性增加的,其大小比活化极化小一个数量级。也就是说,固体氧化物电池储能系统的欧姆电阻导致的电压降很小而且几乎可以忽略,其活化极化等才是电池电压降的主要原因。
本文中,固体氧化物电池构型采用平板型,是具有较高电导率的Ni-YSZ燃料电极支撑的薄膜型电解质YSZ,其空气电极仍然是经典的厚度为几十微米的LSM电极,因此空气电极的欧姆电阻较小。从欧姆极化和活化极化的对比关系可以看出,通过优化电极结构和电极活性是降低极化电阻提高电池性能的主要途径。

Figure 5. The activation polarization resistance of the solid oxide cell system; the operation conditions are at 800˚C, 1 atm and 95% H2/H2O
图5. 固体氧化物电池储能系统的活化过电势,其中操作条件为燃料电极气氛95% H2/H2O而空气电极则为静止空气,操作温度为800℃而系统压力则为常压

Figure 6. The ohimic polarization resistance of the solid oxide cell system with 95% H2/H2O state of charge at 1atm and 800˚C
图6. 固体氧化物电池储能系统的欧姆极化过电势,其中操作条件为燃料电极气氛95% H2/H2O而空气电极则为静止空气,操作温度为800℃而系统压力则为常压
4.1.5. 浓差极化
如图7所示,图中给出了固体氧化物电池在燃料电池和电解池模式下的浓差极化电阻随电流大小的关系。浓差极化主要依赖于两个主要因素,一个是电极微结构,另一个则是系统的操作压力。通常,多孔电极有利于物质输运过程因而可以提高极化性能。本文中,电极结构参照第二章数据,通过计算得到浓差过电势与欧姆过电势处于同一数量级,比活化过电势小一个数量级,即是在100 A电流下也仅达到0.03 V。因此,通过比较固体氧化物电池储能系统的几个主要极化过程,可以得到活化极化仍然是电池系统运行过程中的主要极化损失。
4.1.6. 系统的极化过电势
通过计算固体氧化物电池储能系统的多种极化过电势,可得该系统在燃料电池和电解池模式下运行的电流电压曲线。如图8所示,可以很明显地看到无论是燃料电池模式还是电解池模式,活化极化过电势都是占据主导过程,而欧姆极化过程和浓差极化过程并不明显。因此,对于商业化固体氧化物电池系统的材料和部件,其材料和部件的本身的性能是可以满足商业化要求,而基于这些材料和部件的加工制造技术则是制约固体氧化物电池储能系统性能的关键。而减小极化过电势的途径则更集中在加工制造技术,比如通过调控电极微结构和界面增加活性区域等。
如图8所示,正电流区域属于燃料电池过程,其本质是电化学反应产生电能的过程;而在负电流区域是电解池过程,是进行储能的过程。两个过程之间是完全可逆的,可以从电能的产生向电能的存储进行完全可逆的转变。换句话说,在正电流区域是属于固体氧化物电池储能系统的放电过程,而在负电流区域则是属于系统的充电过程,其充放电的过程也就是电能的存储与利用的过程,而电能在两个过程的往返循环的效率即电能循环效率则是商业化的关键指标之一。
4.1.7. 系统功率
本文假定了系统处于绝热立方体中,但是箱体材料的热导仍然会导致系统出现热损失。固体氧化物
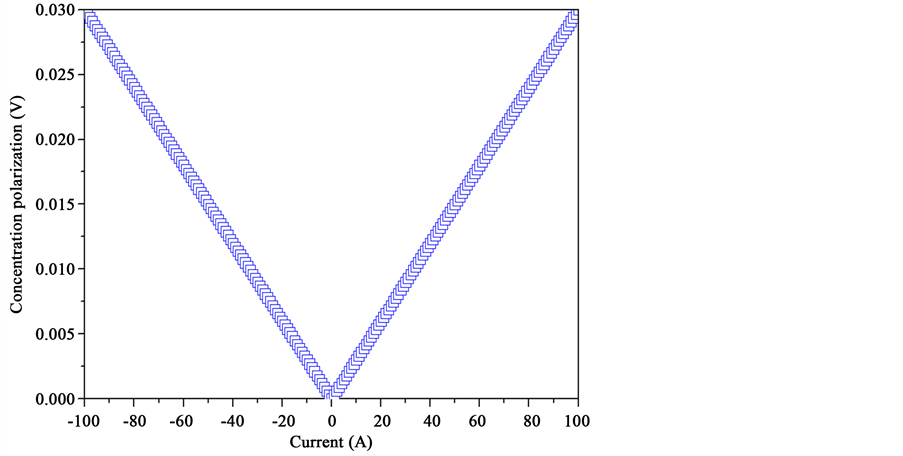
Figure 7. The concentration polarizations of the solid oxide cell system with 95% H2/H2O at 1 atm and 800˚C
图7. 固体氧化物电池储能系统的浓差极化过电势,其中操作条件为燃料电极气氛95% H2/H2O而空气电极则为静止空气,操作温度为800℃而系统压力则为常压
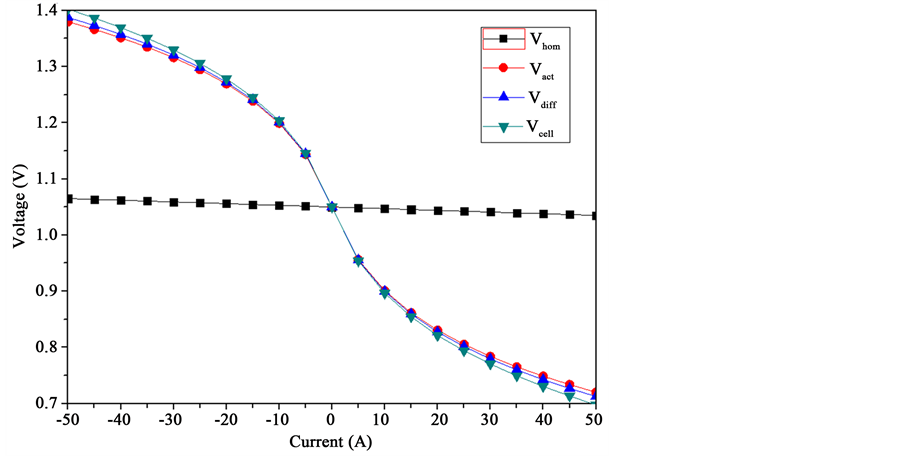
Figure 8. The overall polarizations (I-V curves) of the solid oxide cell system with 95% H2/H2O at 1 atm and 800˚C
图8. 固体氧化物电池储能系统的极化过电势,其中操作条件为燃料电极气氛95% H2/H2O而空气电极则为静止空气,操作温度为800℃而系统压力则为常压
电池储能系统启动运行温度为800℃,而荷电状态为95% H2/H2O,且系统压力为常压。如图9中给出了固体氧化物电池储能系统在燃料电池和电解池模式下的功率曲线,其中正电流区域为燃料电池模式下的系统产生的功率,即放电过程伴随着热能的产生。可以看到,放电状态是一个电能产生的过程,同时也是热能的产生过程,这其中包括电化学反应热和欧姆热等。而在负电流区域,则是固体氧化物电池储能系统处于充电状态,即通过电解池模式将电能存储在燃料中,可以看到其工作过程是一个功率输入的过程,同时也是热量消耗的过程。也就是说,在电解池模式下工作,需要同时输入热能以维持系统的工作
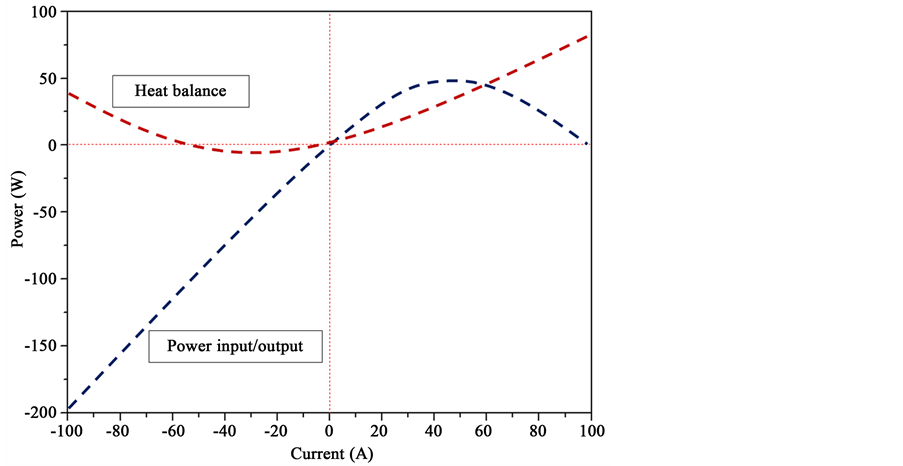
Figure 9. The power out/input of the solid oxide cell system in fuel cell or electrolysis cell mode with 95% H2/H2O at 1 atm and 800˚C
图9. 固体氧化物电池储能系统的功率曲线,其中操作条件为燃料电极气氛95% H2/H2O而空气电极则为静止空气,操作温度为800℃而系统压力则为常压
温度,同时也需要供给电压以实现电能向化学能的转变。可以明显地看出,在相同电流条件下,固体氧化物电池储能系统在电解池模式下的功率输入要远大于其在燃料电池模式下的功率输出。
4.2. 平板固体氧化物电池储能系统热能管理
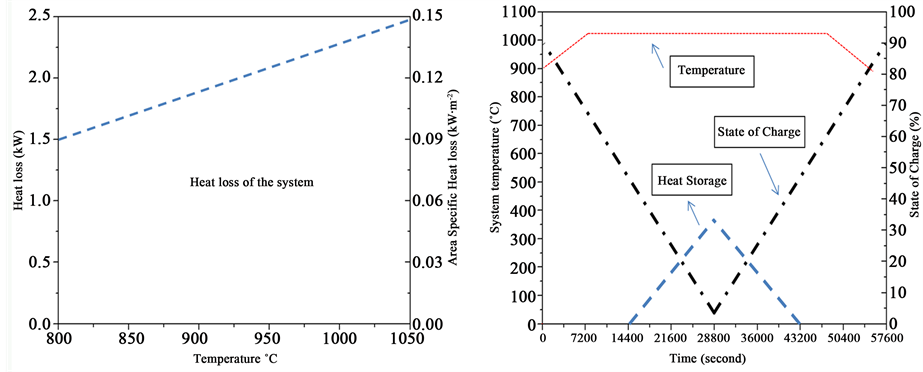
固体氧化物电池储能系统运行过程中涉及了系统热能损失、系统气体热存储、系统材料热存储、系统相变金属热能存储以及由于系统热能存储与损失所导致的系统温度的变化。如图10(a)所示,固体氧化物电池储能系统在操作过程中的热能损失主要与操作温度有关,并且处于线性关系,随温度升高而增加。热能损失主要是用于隔绝系统的金属箱体的导热损失,依据方程(3)~(30),可以看到导热系数一定的情况下,其热能损失主要由系统温度和环境温度的温度差来决定。如图10(b)所示,图中给出了固体氧化物电池储能系统的相关参数包括荷电状态、相变金属热能存储与系统温度的关系。图中曲线属于大约对称型,其左半部分对应于燃料电池模式的工作状态,而右半部分则对应于电解池模式的工作状态。在时间轴为0时,启动固体氧化物电池储能系统进行燃料电池模式放电,荷电状态则随放电状态进行而逐步减小,在电化学热能和欧姆热能的作用下,系统温度开始逐步升高,当达到1010℃时,相变金属则开始吸收热能而系统温度处于平衡不变。
而当相变金属完全融化则实现了热能存储饱和状态,系统温度则开始升高,这时候我们认为固体氧化物电池储能系统放电完成,即将电池系统转换至电解池模式进行充电,即将电能以化学燃料的形式进行存储。从图10可以看到,系统温度在时间轴中部并不变化,因为相变金属存储热能是逐步释放并维持系统运行。充电过程也是增加荷电状态的过程,因此系统荷电状态也会从5%逐步增加到95%而终止。但是,系统在荷电状态在82%时即出现温度下降,即相变金属从液相完全转变为固相并随系统逐步降温而释放热能,最终的平稳温度即为900℃。至此,固体氧化物储能系统完成了放电和充电的一个完整循环,而相变金属也完成由固相到液相、液相到固相的一个完整循环循环,相变金属存储热能维持了系统的高温运行。
通过图10中的数据描述,可以得到完整的固体氧化物电池储能系统的充放电循环和热能循环的利用与管理。通过计算系统循环过程中电能的存储与产生,即可得到电能循环效率这一关键数据。而固体氧化物电池储能系统在燃料电池和电解池模式下的能量效率可由式(33)计算得到,计算结果如图11所示。对于处于可逆状态的固体氧化物电池储能系统来说,其电能效率可以定义为:
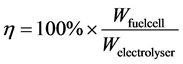 (33)
(33)
其中Wfuelcell的功率输出,Welectrolyser则为电解池模式的功率输入,通过两者对比计算可以得到电能循环效率。而计算所得系统循环效率平均可达80%,已可满足商业化大规模批量化生产的标准。
 (a) (b)
(a) (b)
Figure 10. (a) The heat loss of solid oxide cell system at 1 atm and (b) the relationship between state of charge, energy storage in phase change metal and system temperatures
图10. (a)固体氧化物电池储能系统的热能损失曲线,其中操作压力则为常压;(b)固体氧化物电池储能系统的相关参数包括荷电状态、相变金属热能存储与系统温度的关系
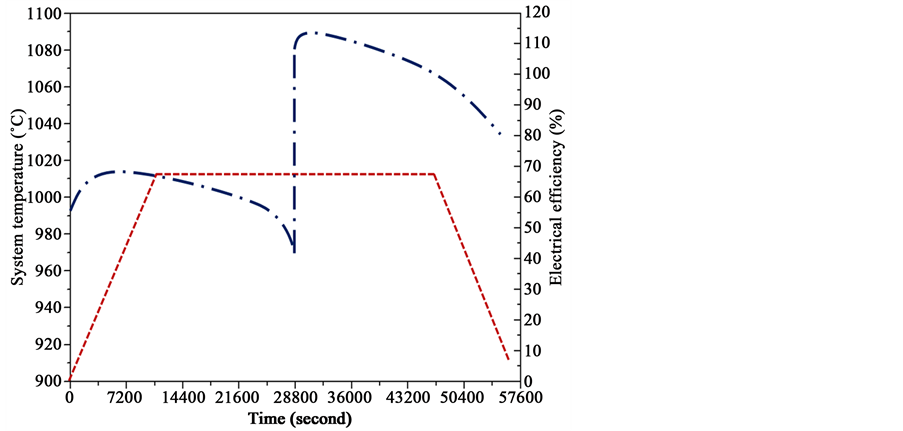
Figure 11. The energy efficiency of solid oxide cell system in fuel cell mode and electrolysis cell mode at 900˚C
图11. 固体氧化物电池储能系统的电能效率,其中操作温度为900℃,考虑相变金属热能存储
4.3. 结论
本文通过建立基于铜基相变金属进行存储与利用的平板固体氧化物电池储能系统的模型,仿真固体氧化物电池储能系统的能量转换过程,研究系统的热能存储与释放,实现电池系统在燃料电池和电解池模式下的放电和充电的循环,评价电池系统的开路电压、活化极化、欧姆极化、浓差极化等对系统热能的影响机制。通过评价相变金属对系统热能的存储与利用,提高系统能量利用效率并最终提高系统的电能循环效率。
研究结果表明电极活化是影响电池性能的关键因素。固体氧化物电池储能系统基于铜基相变金属热能管理后的电能循环效率可达80%以上,满足商业化大规模批量化生产标准的要求。
基金项目
国家自然科学基金重大研究计划:碳基能源转化利用,编号:91545123。

*通讯作者。