1. 引言
玻恩和博特在1954年同获诺贝尔物理学奖 [1] 。众所周知，玻恩是因波函数的统计诠释获奖；而博特获奖是因为用他发明的符合计数法分析宇宙辐射(1925年)，发现宇宙射线并不单是由 射线组成的，从而推翻了以前的传统看法。他们的获奖成就毫无关系。
1924年，博特 [1] [2] [3] 注意到玻尔 [4] 等人关于微观世界也许只有能量和动量的统计守恒的观点，决定用实验来验证其是否正确。他发明符合计数法，并与盖革用此方法共同验证了单个康普顿(电子与X射线的光子)碰撞的能量守恒和动量守恒，即比统计更精确的守恒，否定了玻尔等人只有“不够精确的”统计守恒的观点。还有电子对湮没现象和西蒙(Simon, 1925年)分析用云室记录光子及反冲电子径迹的实验结果，都否定了玻尔等人的观点 [2] 。微观单个事件的系统的能量和动量的守恒律必然会与统计诠释相矛盾。书 [1] 中不仅叙述了玻恩和博特获奖成就，还叙述了博特与盖革验证微观单个事件的守恒律，这说明作者猜测统计诠释与微观单个事件守恒律的矛盾就是他们获奖的联系，也许这样的颁奖安排为以后人们解决这一矛盾留下线索。
由微观单个事件的系统的能量和动量守恒律，一定可以得到统计守恒；反之则不然。在量子力学的许多著作或文集 [2] [5] - [16] 中，只有曾谨言先生的著作 [2] 提到了，微观单个事件的能量和动量守恒律的实验验证，否定了玻尔等人的统计守恒的观点。对于统计诠释与微观单个事件守恒律的矛盾，从量子力学建立到现在，还没有找到哪篇文献或著作想出解决办法。我曾初步讨论过这些守恒的问题1,2，但还是有不足。本文所做的分析要细致些。
沿用至今的量子力学态叠加原理可表述为 [2] [5] ，量子系统可能的状态
，线性叠加后的状态，
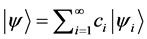(1)
也是该系统可能的状态，其中系数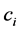
都为复数的概率幅。态叠加原理是与力学量的测量相关的。设
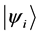为一个粒子的一系列能量本征态，根据量子力学，测量粒子的能量，会以概率
得到相应的能量本征值。对处于这种状态的大量粒子，分别做测量所得到的能量是不一定相同的，或者说是不守恒的，只有能量的统计守恒，即等于期望值，这可以说是统计诠释的直接推广。由这样的态叠加原理得到的单个粒子的状态，就不能满足微观单个测量事件的能量和动量守恒。
本文如作者另外两篇文章 [17] [18] ，希望追求逻辑推理的严格性，而不能够追求论证的“数学严格性”，正如朗道和栗弗席茨的书中所说 [6] [19] ，数学严格性的追求在理论物理中往往是自欺欺人。因自由粒子不存在，任何粒子总与环境相互作用。所讨论的单个粒子总是复合系统的一部分，因此，严格来说，态叠加原理应该用于有相互作用的复合系统中，不仅如此，也容易满足微观单个测量事件的能量和动量守恒。因为相互作用可以使复合系统中各部分交换能量和动量；若测得一部分的能量大，那么测得其它部分的能量或能量之和就小，每次加起来，总和就可以满足守恒；动量也类似。只看其中的单个粒子，就只能得到统计守恒，并且，单粒子叠加态是近似的，不是严格的1,2 [17] 。
本文第2部分对统计诠释与微观单个事件守恒律的矛盾做较详细的分析。第3部分提出对态叠加原理的修改建议，从而消除统计诠释与微观单个事件守恒律的矛盾，使它们在量子力学中得到兼容。第4部分简单介绍有人设想并有实验验证的停止相互作用后的纠缠，即存在非定域性的纠缠；运用本文修改的态叠加原理和物理学定义，质疑那些对非定域性纠缠的实验验证。最后是结论。
2. 统计诠释与微观单个事件守恒律的矛盾及分析
从实验的误差考虑。在较高能的情形，因为所研究的系统受外界环境噪声的影响相对较小，那么，在较小的实验误差范围内，容易验证微观单个事件中系统的能量及动量守恒，例如单个康普顿碰撞。而低能的情形，系统受外界环境噪声的影响相对较大，实验上的误差就足以破坏系统的这些守恒，所以只能得到统计守恒。
再按不同叠加态来做以下三点分析。第一，到现在，量子力学理论一直不提态叠加原理与相互作用是否相关，或者认为与相互作用无关。由此可以得到自由粒子(理论上外推假设的)不同动量或动能的本征态的叠加，例如(1)式，但这不可能有单个事件或单次测量能量或动量的守恒，只能有统计守恒。第二，对于没有相互作用的两个自由粒子构成的复合系统，量子力学认为其状态可以由动量本征态
叠加得到
， (2)
其中系数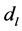
为复数的概率幅，若上式有两项或多于两项，则两个粒子系统处于纠缠态 [2] (即不能表示为粒子1态
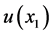与粒子2态
的乘积态或直积态
的系统状态，称为纠缠态)。设两个粒子的动量满足条件
， (3)
则同时测量系统的两个粒子的动量，有每一次测量动量之和守恒，自然也有统计守恒；但态叠加原理允许
，则测量动量之和只能统计守恒。因没有相互作用能，能量(即动能)的分析也类似。若只测量一个粒子的动量或动能，就只能得到统计守恒。这里做一个数学上的猜想，满足和不满足条件(3)式的两个粒子的动量本征态，有可能通过(2)式的形式叠加得到相同的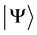
。反过来看，态
又该如何按两个粒子的动量本征态展开？即测得一个粒子的动量
后，立即测量另一个粒子的动量，是否一定得到满足(3)式的对应动量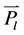
？
第三，由两粒子构成的有相互作用的复合系统，动量的分析与第二点类似，可以把系统的状态展开为(2)式。还需说明一下，每一项
都可以按系统的能量本征态来展开，也得到系统的一个可能的状态。因相互作用能属于复合系统，单个粒子的动能还可以定义，但其能量就没有定义，只能定义系统的能量。若系统状态由两个粒子的动能本征态
(这不是系统的能量本征态)叠加，可以得到
， (4)
其中系数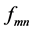
为复数的概率幅。设两个粒子的动能可以满足条件
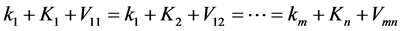， (5)
两个粒子分别处于
和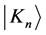
态时，相互作用能
也为确定值，即满足(5)就可以有单次测量系统能量的守恒。但态叠加原理也允许(5)式不成立，测量系统能量就只有统计守恒。在已知两个粒子系统状态的前提下，也可以按一个粒子的某一力学量本征态来展开 [20] 。例如系统状态
按第一个粒子的动能本征态(用分立谱来说明)
展开，则
， (6)
其中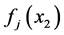
为展开系数，是与第二个粒子相关的波函数。在数学上，也猜测会有形如(4)式的四种可能：(3)式(即动量守恒)成立而(5)式成立和(5)式不成立的两种情形，(3)式不成立而(5)式成立和(5)式不成立的两种情形。哪种情形正确？因不确定度关系，在某一位置
，测第一个粒子的动量是预先完全不确定的；当测得第一个粒子某一动量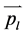
后，按波包塌缩，立即测量第二个粒子，即在某一位置
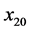测到第二个粒子，是否可以得到确定的动量
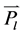？同样，在某一位置
，测第一个粒子的动能是预先完全不确定的；当测得第一个粒子的某一动能值
后，在某一位置
测到第二个粒子，是否可以得到确定的动能与系统的势能之和？
在量子光学 [21] 中，对于原子与单模光场相互作用的复合系统，做旋波近似后，其状态为
，原子基态
与激发态
的能级差为一个光子的能量，
为
个光子数态。单
次测量能量，使系统状态塌缩为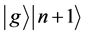
或
，能量都相同，即守恒。这可以说基态原子吸收一个光子后，系统由状态
，反之亦然。但是，没有做旋波近似，就会出现如：
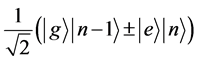等系统状态。这些都是态叠加原理或量子力学所允许的。对于
，可以说基态原子放出一个光子后，系统由状态
，或激发态原子
吸收一个光子后，系统由状态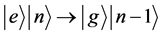
。这些又如何解释？
相互作用无处不在，自由粒子是不存在的，一个粒子总要与环境相互作用，粒子总是一个大的有相互作用的复合系统的一部分或子系统。大物体或强场与粒子相互作用的复合系统中，粒子的状态变化大，而大物体或强场状态的变化相对很小，或者说大物体或强场的状态可看成近似不变。再把相互作用能看成粒子在外场中的势能，就可以由复合系统的薛定谔方程近似得到单个粒子的方程。因此，复合系统的薛定谔方程应当被看作基本假设，而单个粒子的薛定谔方程都应看作是近似的。
我的文章 [17] ，一类近似等式与单个粒子相干叠加态的概念性讨论中，写出了一类近似等式
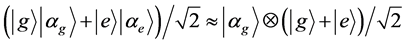(7)
上式左边是阿罗什等人 [22] 的文中(单个原子通过一个分束器，即处于相干态的微波脉冲)给出的，是原子与分束器构成的复合系统演化成的纠缠态，这里也用
和
分别表示原子的基态和一个激发态，
和
为分束器的两个相干态。他们认为，在经典近似下，有
[22] ，但没有写出(7)式。
文章 [17] 得出结论：有相互作用的两部分组成的复合系统一般演化为纠缠态。若复合系统由粒子和大物体或强场组成，后者的状态近似不变，纠缠态可以近似为直积态(例如(7)式)。自由粒子是不存在的，但从理论上说，可以外推，做两种假设，一种是自由粒子既可以处在动能本征态又可处在其相干叠加态；另一种是它只处于动能本征态。认为假设后者更合理。要制备单个粒子的叠加态，可以由包含这个粒子的复合系统的纠缠态近似为直积态来得到，这可能是唯一的途径。文中所举的三个例子是，原子与双缝物体相互作用，光子与极化(偏振)分束器相互作用，电子与斯特恩–盖拉赫实验装置中特定的非均匀磁场相互作用，三个复合系统都分别处于纠缠态。都做近似，分别得到原子的两个“路径态”的相干叠加态，光子的两个垂直偏振态的相干叠加态，电子的自旋向上态和向下态的相干叠加态。
举宏观例子说明，用球拍对着桌面击打乒乓球，不看乒乓球与球拍和桌面的相互碰撞作用，只看乒乓球在中间的上下过程，就会觉得奇怪，反直觉；其实人们立即会想到相互作用，这就不奇怪，不反直觉！再如1996年实验得到的薛定谔猫态 [23] ，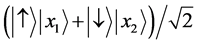
，离子处于不同的内部态
和不同位置态
的纠缠态；考虑到激光对离子的作用，就不奇怪，不反直觉了！
3. 对态叠加原理的修改建议
本文建议对态叠加原理的表述增加两个限制，即此原理用于有相互作用的复合系统中并满足微观单个事件的守恒律。
如上所说，单个粒子的叠加态，只能由它与大物体或强场相互作用的复合系统的纠缠态，做大物体或强场的状态不变的近似得到。按以上修改的态叠加原理，复合系统的纠缠态，在形式上，可以写成满足条件(3)式的(2)式，即动量本征态的叠加。单次测量粒子和大物体(或强场)的动量，它们的和是守恒的(当然大物体或强场的动量是难以测量出变化的，这只是提出一种可能的理解，总比只能理解到统计守恒要好些)。再把相互作用能看作粒子在外场中的势能，则粒子能量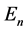
和大物体动能
或强场能量的本征态的叠加，有如下形式
， (8)
满足条件
，单次测量粒子的能量和大物体的动能或强场的能量，它们的和就是守恒的。而单看粒子的能量，就只能统计守恒。这样，对单个粒子情形就兼容了微观单个事件的能量守恒和动量守恒与统计诠释。
对于有相互作用的两个粒子复合系统，如上所述的第三点情形，相互作用使两个粒子之间等量交换动量，而能量则是在两个粒子的动能以及相互作用能三者之间等量交换，这是我们可以理解的；而非等量的交换是不可理解。按以上修改的态叠加原理，在某一位置
，当测得第一个粒子某一动量
(或动能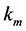
)后，立即测量第二个粒子，可以在某一位置
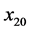，确定地测得第二个粒子的动量(或动能与系统势能之和)。可以认为不确定度关系适用于先测量的粒子，而紧接着在测量到的第二个粒子的位置上，测量动量(或动能与系统势能之和)就是确定的了。这样，单次测量两个粒子的动量之和就是守恒的，单次测量系统的能量(即两个粒子的动能与相互作用能三者之和)也是守恒的。若只测量一个粒子的量，就只能统计守恒。
对于类似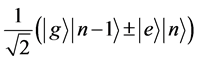
的系统状态，测量能量只能统计守恒。而实际上可以理解为
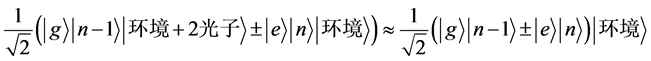， (9)
这样，单次测量这个大系统各部分的能量，那么能量之和就是守恒的。
再考虑下面的，对于停止相互作用后的两个自由粒子构成的复合系统的分析，就可以消除微观单个事件的守恒律和统计诠释的矛盾，使它们在量子力学中得到兼容。
4. 相互作用与非定域性的简单讨论
对于停止相互作用后的两个自由粒子构成的复合系统，按沿用至今的态叠加原理，其状态可以表示为，由两个粒子的动量(或动能)本征态的直积为基矢叠加得到(2)式(或(4)式)的形式。若存在两项或多于两项，则为纠缠态。这种停止了相互作用，两个粒子间距可以近也可以远，纠缠被认为依然存在的系统状态可以说具有非定域性。对这种非定域性纠缠，从实验上看，“同时”测量两部分，总有一先一后，要求两个测量的时间差比光速走它们的间距用时要短，即最大传递信息的光速还来不及传递信息，就得到了两部分高关联程度的测量结果(下段做分析)；理论上，无论那部分先测量，都引起系统状态的“波包瞬间塌缩”，可得到高关联程度的测量结果。从纠缠态的形式(2)和(4)上看，停止了相互作用的两个粒子之间还可以交换动量和动能，并且，由前面的分析，既可以有满足(3)式的叠加，又可以有不满足(3)式的叠加，或者说，既可以存在等量的交换，也可以存在非等量的交换，这种非定域性纠缠在经典物理中都是不可理解的，或是与经典物理相冲突的。
这里进行关联程度的一个简单分析。若存在着停止相互作用后保持纠缠(即存在非定域性的纠缠)的量子态，应该测得其关联程度高于75%，理想情况为100%，而非纠缠态的关联程度低，不超过75%。考虑两个初始纠缠的电子或光子，当互相远离，停止相互作用后，如果这两个电子的状态还存在纠缠，可以测得较高的关联；如果不存在纠缠，只能测得较低的关联，即不存在非定域性。例如，停止相互作用后，两个电子仍处于纠缠的自旋单态1
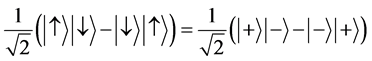， (10)
其中
为自旋按 轴，一个电子向上和一个向下态，
为自旋按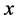
轴正向和负向态，这个自旋单态可以写成这两种形式。那么，对两个电子沿
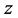轴方向测量自旋取向，当一个测得自旋向上，另一个就一定向下，反之亦然，即反关联程度为100%；若沿
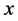轴方向测量，当一个测得自旋为正向，另一个就一
定为负向，反之亦然，反关联程度也为100%。如果不存在纠缠，简单假设，两个电子的态为以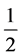
概率处于
态和以
概率处于
态的混合态。进行以上同样的测量，沿 轴方向测量自旋取向，当一个
测得自旋向上，另一个就一定向下，反之亦然，即反关联程度还是100%；但是，沿
轴方向测量，当一个测得自旋为正向，另一个只有50%的概率为负向，反之亦然，反关联程度降为50%。总体平均就是75%。这样的测量就可以判断是否存在非定域性。
加上相互作用这一限制条件的态叠加原理，把两个没有相互作用的自由粒子视为复合系统，就只有两个粒子动量(或动能)本征态的直积态，而没有纠缠，没有交换动量和动能的问题，分别单次测量两个粒子的动量或动能自然会守恒，动量或动能之和也会守恒；并且测量得到的关联程度低，没有非定域性。
物理学的定义或研究对象是，研究物质结构，物质运动和物质之间的相互作用的学科。可以说相互作用比统计诠释和微观单个事件的守恒律，以及态叠加原理更为基本，更为重要。
爱因斯坦等人 [20] 与玻尔 [24] 争论的两个焦点分别是实在性和定域性。爱因斯坦等人的实在性与相互作用无关，玻尔的反驳，恰恰用了测量仪器与被测粒子的相互作用。爱因斯坦等人由量子力学态叠加原理和薛定谔方程，得到他们所不能理解的与相互作用无关的纠缠，即存在非定域性的纠缠，并以此来质疑量子力学的完备性，而与相互作用有关的纠缠(即定域性的纠缠)是他们及其他人 [6] [19] 所认可的；相反，玻尔的反驳，用了与相互作用无关的互补性原理。单用相互作用来判断，爱因斯坦等人的实在性是错的，玻尔的反驳是对的；爱因斯坦等人的定域性是对的，玻尔的反驳(即支持非定域性)是错的。
设想本文提出修改的与相互作用有关的和服从微观单个事件的守恒律的态叠加原理，出现在爱因斯坦与玻尔争论之前，可能就不会在理论上设想出没有相互作用的纠缠，来质疑量子力学的完备性。
在量子力学的论著中，我只看到曾谨言先生的著作 [2] 中提到微观单个事件的守恒律，而其它许多著作都没提，这似乎是被绝大多数人忘却或回避了？也许正是这种忘却，在最近四十多年的文献里，没有相互作用的纠缠或存在非定域性纠缠得到了一边倒的实验 [25] - [30] 认可，尽管前三十多年的实验文章都承认他们的实验验证都是有漏洞的，即测得有漏洞的高关联，但没有发现哪篇文章报道，低关联的实验验证。这是令人质疑的。2015年的好几篇文章 [31] [32] [33] [34] [35] 都声称无漏洞地实验验证了非定域性的纠缠态，并要对此做盖棺定论 [36] 。最近的一篇文章中 [37] ，作者仍然坚持认为，那些声称无漏洞的实验不可以被称为完全没有漏洞，这与本文的分析有所不同，但都表明了怀疑的态度。若存在非定域性的纠缠态，那么，态叠加原理加上相互作用的限制就是错误的，微观单个事件的守恒律就不能被量子力学理论所容纳。
5. 结论
为了满足微观单个事件的系统能量守恒和动量守恒，并因为实验中真正制备单个粒子的叠加态与相互作用有关，本文对态叠加原理提出修改建议，其表述中需增加两个限制，即此原理用于有相互作用的复合系统中，并满足微观单个事件的系统能量和动量守恒律，这可以消除这些守恒律和统计诠释的矛盾，使它们在量子力学中得到兼容。运用这种修改，对于单个粒子的相干叠加态和存在相互作用的复合系统纠缠态(即定域性的纠缠态)等量子现象的解释，就符合或接近直觉；而对于停止相互作用后继续保持纠缠或存在非定域性纠缠这类反直觉的所谓量子现象所进行的实验验证，会表示质疑。
致谢
感谢北京师范大学裴寿镛教授，刘小明、王海波副教授，南京大学金国钧教授，国防科学技术大学李承祖、梁林梅教授，中科院理论物理所刘纯教授，江西师范大学嵇英华教授，我的同事邵彬、邹健、邢修三、张向东、姚裕贵、韦浩、苟秉聪、王锐、江兆潭、杨帆等教授，李军刚、王锋、缪劲松、蔡金芳、鲁长宏、苏文勇、冯艳全等副教授，宋新兵讲师，感谢他们能与我讨论，或提供帮助，或提出质疑。我还要感谢我的老师吉林大学丁培柱、潘守甫教授、兰州大学江先国教授，我的同学应立凡、李桂琴的鼓励和支持。
基金项目
国家自然科学基金(11075013, 11375025)资助。
NOTES
1Zeng, T. H. New understandings of quantum mechanics based on interaction. arXiv:1008.1691.
2Zeng, T. H. Attempt at perfecting quantum mechanics based on interaction. arXiv:1307.1851.