1. 前言
近年来灰色预测、决策与灰关联系统等应用于决策模式的研究受到广泛的注意,文献 [1] 用灰色GM(1,1)模型对林分平均生长过程进行模拟,给出落叶松人工林林公在树高,胸径,材积3个指标上平均总生长量的灰色模型,经过检验,估测效果显著。在文献 [2] 中,运用灰色预测来预测大学人数的增减。房价是影响商品房供需的重要因素,房价的高低和变化趋势关系到百姓的居住条件能否切实改善和以住宅产业拉动内需政策能否取得预期的成效。为保证住宅产业的健康发展,及时掌握商品房房的价格动态,并对市场价格的变化趋势做出科学的预测是十分必要的。由于影响商品房价格的因素很多,它们之间的关系错综复杂,难以阐述清楚,但我们可以得到商品房平均销售价格的历史数据,这些历史数据实际上是过去各种确知的和不确定的信息的综合反映,因此商品房房价完全可以用历史数据作为灰色信息的反映来进行分析、研究确定其变动规律,从而确定出其未来的趋势。本文探讨了利用GM(1,1)灰色预测模型 [3] - [11] 对商品房价格进行预测,并取得较好的预测效果。
2. 基本方法
2.1. 生成函数
在建立灰色预测模型之前,需先对原始时间序列进行数据处理,经过数据处理后的时间序列即称为生成列。
累加生成:通过数列间各时刻数据的依个累加得到新的数据与数列。累加前数列为原始数列,累加后为生成数列,其基本关系式如下:
记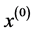 为原始数列:
为原始数列: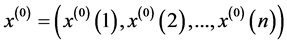 ,
,
记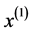 为生成数列:
为生成数列: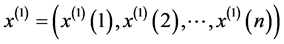 ,
,
如果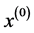 与
与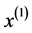 之间满足下列关系,即
之间满足下列关系,即
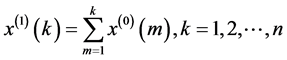

称为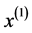 为序列
为序列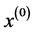 的一次累加生成。
的一次累加生成。
2.2. 灰色GM(1,1)模型
灰色系统理论通过对一般微分方程的深刻剖析定义了序列的灰导数,从而进一步建立了灰色GM(1,1)模型。灰色系统分析首先必须对系统信息作累加生成。累加生成所建立的生成函数则是系统建模与预测的基础。灰系统理论认为概括所有系统皆属广义能量系统,且符合指数律运算,则生成函数便可用下列方程式来替代:
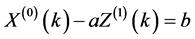
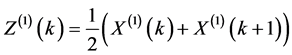
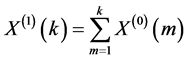
上式称为一次累加生成(1-AGO)。
时间序列为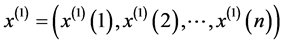
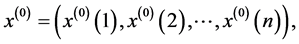 为
为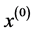 的一次累加生成,则称
的一次累加生成,则称
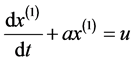 (1.1)
(1.1)
为GM(1,1)模型,即灰色微分方程模型。
式(1.1)中,其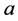 称为发展系数;
称为发展系数;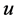 称为灰色作用量。先引进下述记号:
称为灰色作用量。先引进下述记号:
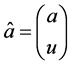 (1.2)
(1.2)
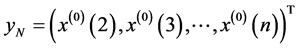 (1.3)
(1.3)
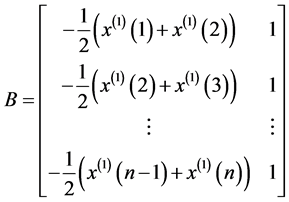 (1.4)
(1.4)
可利用最小二乘法求解,则有:
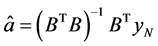 (1.5)
(1.5)
从而可求出(1.1)式中的参数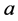 与
与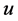 ,(1.1)式的预报模型为:
,(1.1)式的预报模型为:
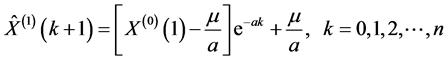 (1.6)
(1.6)
 (1.7)
(1.7)
式(1.6)与(1.7)可用于预测未来值和检验模型精度。
2.3. 灰色关联分析
灰关联分析(Grey Relational Analysis)是灰色理论中分析离散序列间的相关程度的一种测度方法。也就是对灰色系统因素间的发展动态进行定量比较分析,分析那些因素是主要的,那些因素是次要的。且灰关联分析,具有少数据及多因素分析的特点,刚好可以补强传统统计回归上的缺点。
假设此研究变量中的任何一个序列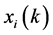 均可为参考序列时,所以使用整体性(Globalized)灰关联度,并将其研究步骤简述如下:
均可为参考序列时,所以使用整体性(Globalized)灰关联度,并将其研究步骤简述如下:
1) 两比较序列之绝对差:
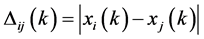
其中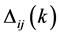 为
为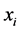 和
和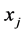 之间第k个差的绝对值、
之间第k个差的绝对值、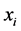 为参考序列、
为参考序列、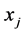 为其它比较序列。
为其它比较序列。
2) 求得所有比较序列在各点的绝对差中最小值与最大值:
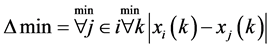
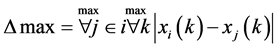
3) 计算灰关联系数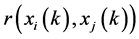 :
:
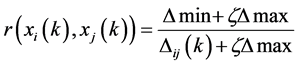 (1.8)
(1.8)
其中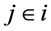
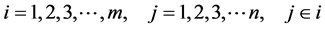 ,带入两级最大差、最小差及辨识系数
,带入两级最大差、最小差及辨识系数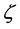 :其中辨识系数
:其中辨识系数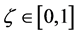 ,其值可依实际需要调整。主要功能是作背景值和代测物之间的对比,其大小可以根据实际的需要作适当的调整。由实际的数学证明中得知只会改变相对数值的大小,不会影响灰关联度的排序。一般来说,
,其值可依实际需要调整。主要功能是作背景值和代测物之间的对比,其大小可以根据实际的需要作适当的调整。由实际的数学证明中得知只会改变相对数值的大小,不会影响灰关联度的排序。一般来说,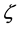 值皆取在0.5附近。
值皆取在0.5附近。
4) 辨识系数
在关联系数中,辨识系数(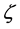 )的功能主要是做背景值和待测物之间的对比,其大小可以根据实际的需要做适当之调整,由实际的数学证明中得知辨识系数值会改变相对数值的大小,不会影响灰关联排序,对于下面这个式子:
)的功能主要是做背景值和待测物之间的对比,其大小可以根据实际的需要做适当之调整,由实际的数学证明中得知辨识系数值会改变相对数值的大小,不会影响灰关联排序,对于下面这个式子:
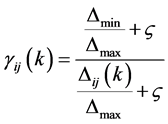 (同除以)
(同除以)
由于数据处理使得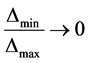 ,所以:
,所以:
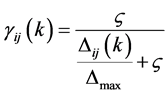
5) 计算灰关联度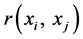 :
:
当求得灰关联系数后,假设各因子权重相同时,一般取灰关联系数的平均值为灰关联度,即为:
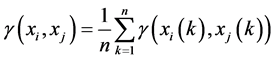 (1.9)
(1.9)
3. 应用与分析
如表1,表2所示。
为了便于比较时间间隔的大小对建模精度的影响,下面分析时间间隔为一年与两年取样分别建模,以作比较。

Table 1. Shanghai calendar year commodity house average sales price (1)
表1. 上海市历年商品房平均销售价格(1)

Table 2. Shanghai calendar year commodity house average sales price (2)
表2. 上海市历年商品房平均销售价格(2)
3.1. 按时间间隔为一年建模
令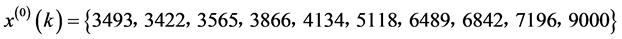 ;运行该程序得到下图:
;运行该程序得到下图:
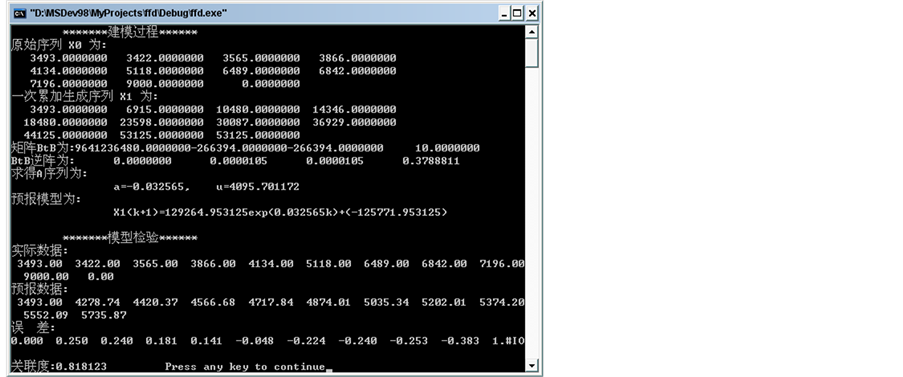
其中GM(1,1)模型为:
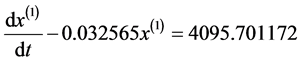
即预报式为:129264.953125 E 0.032565K − 125771.953125
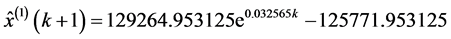
3.2. 按时间间隔为两年建模
令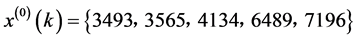 ,利用同样方法代入程序,运行得下图:
,利用同样方法代入程序,运行得下图:
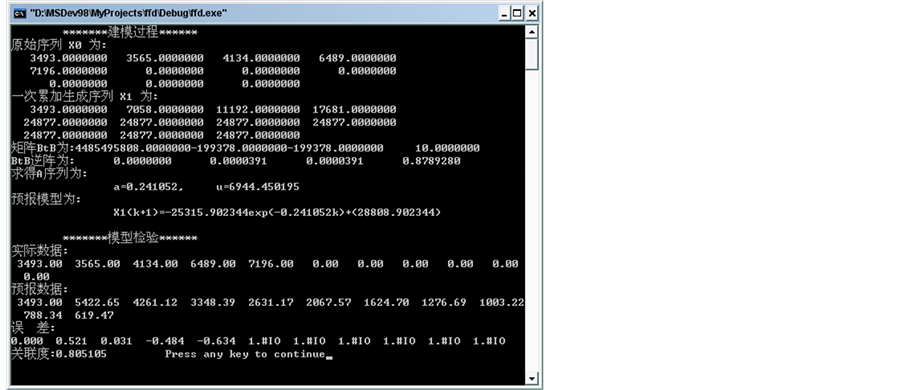
其中GM(1,1)模型为:
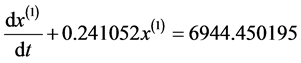
预报式为:
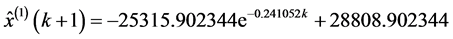
3.3. 模型的检验
由上面两个程序运行的结果来看,很显然取样间隔对结果影响较大,如下面两个对比图可知。从误差值的大小可以看出,前一表中的误差小一些,而后一图的误差大。这说明取样间隔越小,模型精度越高,此外,最后每个图中还求出了关联度,它们是取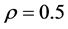 进行检验的,由于关联度的值分别都很理想,且:
进行检验的,由于关联度的值分别都很理想,且: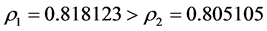 ,进一步说明取一年时间间隔建模效果好。
,进一步说明取一年时间间隔建模效果好。

