
1. 引言
由于水平井在单井产量、经济效益以及在非常规油气勘探中的优势明显,所以应用十分广泛。当前水平井钻井技术的挑战之一是实时地质导向 [1] [2] [3] [4] 。水平井钻前地质模型具有一定的不确定性,故随钻实时地质导向对于提高储层有效钻遇率显得极为必要,而实时地质导向的关键在于实时预测地层界面 [3] [4] 。国内常用随钻自然伽马测井和电阻率测井方法进行地质导向,随钻电阻率因其探测深度较深,常用于确定地层界面。但在低阻、低对比度储层或薄层中,因受到围岩影响,随钻电阻率用于指示地层界面的可信度降低,而自然伽马具有更高的分辨率,在上述储层中可以较为准确地指示岩性和界面 [5] [6] [7] [8] 。目前,常用蒙特卡洛等方法对随钻伽马测井进行正反演研究。考虑到该类方法的计算速度和时效性问题 [5] [9] [10] ,该次研究首先基于地层中自然伽马强度的分布原理,分析了常规伽马测井的响应模型,然后根据水平井中随钻伽马测井探测范围的空间特征,确立了水平井中随钻自然伽马测井的正演方法;利用该正演方法,确定了在不同伽马特征的地层中,离地层边界不同距离情况下的随钻自然伽马测井响应图版;然后利用该图版,建立了随钻伽马测井快速反演储层界面的方法。在不同伽马比例的双层介质模型中进行测试,该方法可快速反演出地层界面;将该方法应用在理论地层模型和随钻实例地层中,可以快速、准确地反演出地层界面的位置。因此,该方法可用于指导随钻伽马测井的实时地质导向工作。
2. 随钻伽马测井和正演模型
2.1. 随钻伽马测井
自然伽马测井是用于测量地层天然放射性伽马射线强度的测井方法 [10] 。在原理上,随钻自然伽马与常规伽马测井方法类似,常用于指示水平井井周的地层岩性和界面,在薄层、低阻储层的随钻地质导向中应用广泛 [5] [7] [8] [10] 。通常,随钻仪器中伽马测量短节会采用近钻头测量方式,近钻头测量能准确无滞后地测量钻头处的储层伽马特性,及时确定地层和边界位置,根据地质信息调整井眼轨迹,实现实时的地质导向 [8] [11] 。
2.2. 无限均匀介质自然伽马响应模型
考虑地层模型为无限均匀介质,设地层密度为ρ,每克岩石中含q克放射性物质,每克放射性物质每秒发射的伽马光子数为a,地层对伽马光子的吸收系数为μ,取球坐标系(见图1),那么体积元dv在距离为r的观测点处产生的射线强度为 [5] [10] :
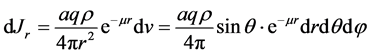 (1)
(1)
式中:Jr为自然伽马通量,s−1∙cm−2;a为伽马光子数,g−1∙s−1;q为每克中含岩石放射性物质的质量分数,g/g;ρ为地层密度,g/cm3;r为观测点的探测距离,cm;μ为地层对伽马光子的吸收系数,cm−1;v为球坐标微元体积,cm3;θ为球坐标天顶角,(˚);φ为球坐标方位角,(º)。
对式(1)积分后可得均匀球体空间在球心观测点产生的自然伽马通量:
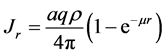 (2)
(2)
根据式(2),假设探测点处99%的自然伽马通量由半径为R的球体造成,则有1−e−μr = 0.99,由此可得μr = 4.065,从而根据不同地层的μ计算出相应的R。一般自然伽马测井仪器设计的探测深度约为0.3 m,如果考虑套管、钻杆、钻井液等因素影响,仪器实际探测深度一般为0.2 m左右 [5] [10] [12] ,该次研究设定探测深度R = 0.3 m。
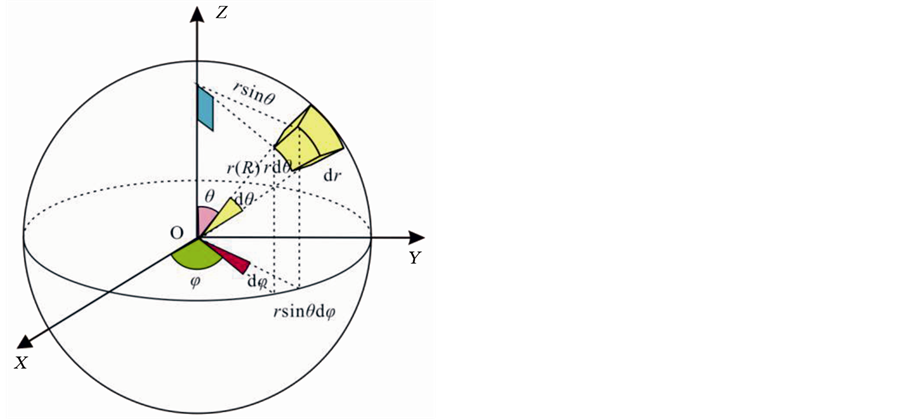
Figure 1. Schematic of natural gamma detection range in spherical coordinate system
图1. 自然伽马探测范围球坐标系积分示意图
2.3. 水平井层状地层自然伽马测井正演模型
邵才瑞等 [5] [6] [10] 分析了水平井中随钻伽马测井的探测范围与地层空间系(图2),基于伽马射线在地层中的衰减规律,建立了随钻伽马仪器位于地层不同位置和不同地层模型中的快速正演算法。考虑到储层厚度通常是随钻伽马测井探测直径的数倍 [2] [6] [13] ,该次研究中薄层情况不予考虑,故图2中受到地层1和地层2的界面影响时,仪器探测范围内不同区域(A、B、C)的伽马射线强度为:
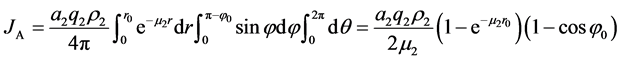 (3)
(3)
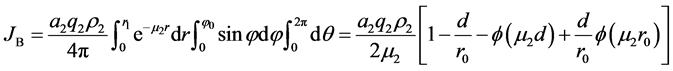 (4)
(4)
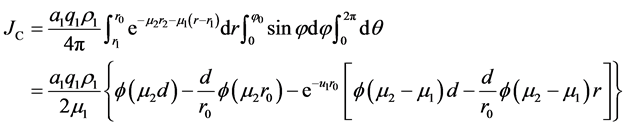 (5)
(5)
式中:JA、JB和JC分别代表图2中A、B和C三个体积域在观测点O处的伽马射线强度,s−1∙cm−2;参数a、q、ρ、μ的下标1、2与图2中的地层序号1、2一致;r0为探测深度,cm;φ0为图2中地层界面与探测范围的夹角,(˚);d为探测器到地层界面的距离,cm;f是金格函数。
上述算式中使用的金格函数 [12] :
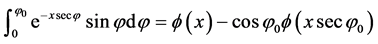 (6)
(6)
式中:x为金格函数变量,1。
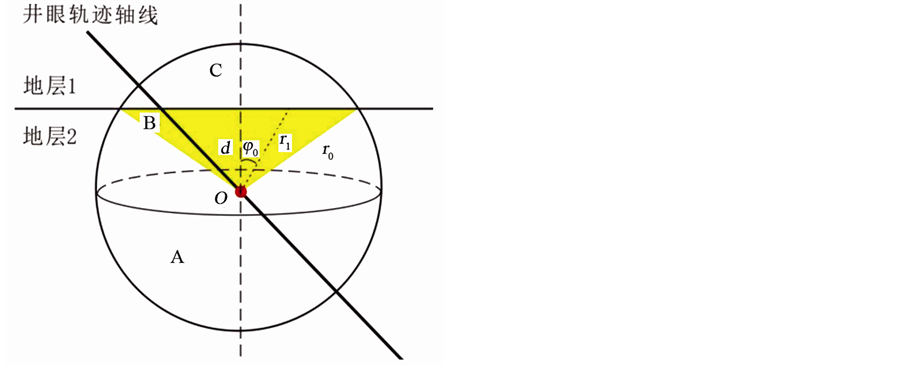
Figure 2. Schematic of gamma detection in transverse isotropic sandstone and mudstone
图2. 横向各向同性砂岩、泥岩层状地层伽马探测示意图
3. 随钻伽马测井快速反演储层界面方法
随钻伽马测井正演模型无法直接用于储层界面距离的反演,假设随钻伽马仪器由地层1 (砂岩)穿过界面进入地层2(泥岩)时(图2),设界面处仪器离界面距离为0,在界面之上和之下时d分别为负值和正值,利用上述正演模型模拟出离界面距离不同时自然伽马强度的分布情况(图3)。由图3可以看到,当d大于0.3 m后,仪器响应几乎不受影响,因此在界面附近0.3 m处自然伽马响应才能反映出界面的影响;当界面上、下地层自然伽马比值一定时,随钻伽马仪器响应是该比值的确定函数;当地层1与地层2的自然伽马比值C为1:12时,离界面的距离是伽马不同比值的函数,当C为其他值时,可以看到随钻伽马测井具有类似的响应特征曲线。因此,图3可以作为确定随钻伽马离界面距离的图版使用。
为快速获取储层界面信息,利用该图版建立快速反演模型,当C = 1:12时,在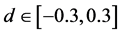 区域,可获得较好的拟合曲线(相关系数近似为1),如图3中红色虚线所示,公式如下:
区域,可获得较好的拟合曲线(相关系数近似为1),如图3中红色虚线所示,公式如下:
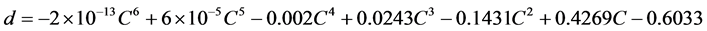 (7)
(7)
 类似地,可以获得不同C情况下d的函数,建立起离界面距离的快速反演方法。
类似地,可以获得不同C情况下d的函数,建立起离界面距离的快速反演方法。
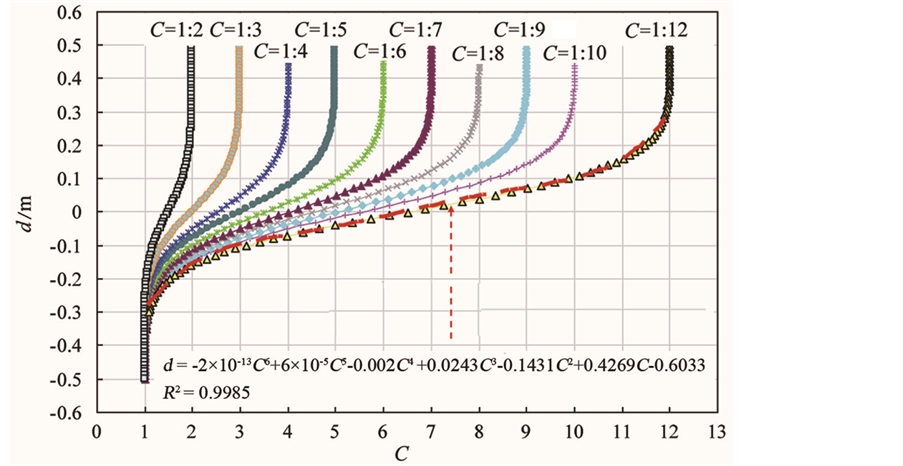
Figure 3. Response characteristics of gamma ray logging while drilling in different locations and different formations
图3. 在不同地层水平井中随钻伽马离界面不同位置时的响应特征
4. 界面快速反演测试
为测试该快速反演储层界面方法的正确性,分别利用理论地层界面模型和现场实例来验证该方法的有效性。
4.1. 双层介质模型界面反演
建立理论层状地层模型(图4),水平井轨迹从上往下穿过泥岩层(150API)和砂岩层(30API),依据水平井轨迹穿过该地层的情况,利用式(3)~(6)正演计算得到图中的自然伽马测井响应特征;再利用上述快速反演储层界面模型,反演得到图4中离界面的距离情况,可以看到,在随钻自然伽马测井探测范围内(0.3 m),离界面的距离随水平位移变化曲线与井轨迹几乎重合,对比实际界面的距离绝对误差仅0.01 m,证明了快速反演方法的准确性。
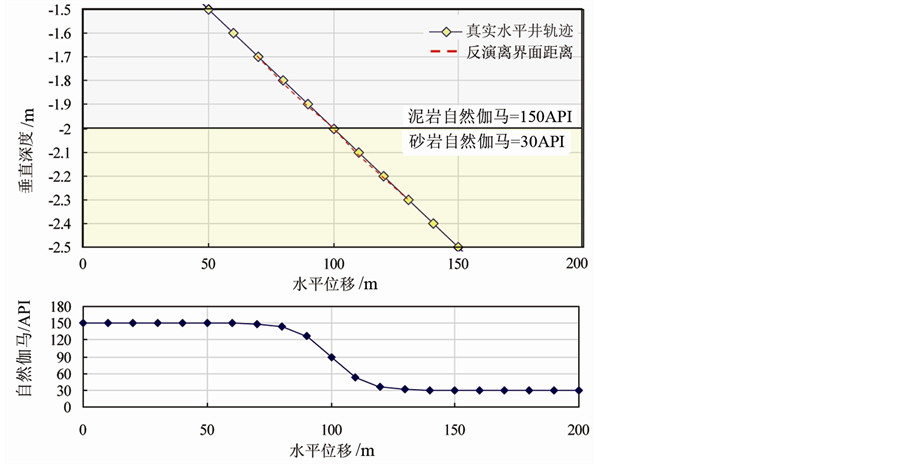
Figure 4. Logging responses in theory layered formation model
图4. 理论层状地层模型中的响应特征
4.2. 实际地层界面反演
新疆油田某水平井S井,选取水平井轨迹靠近储层边界的深度段,为清晰显示界面反演深度段的对比情况,选择井轨迹起点为1000 m的垂直深度,位移起点为0 m,可以观察到在水平位移约20 m时,井轨迹钻遇界面,且上方泥岩层自然伽马为107API,下方砂岩层自然伽马为53API;考虑到随钻自然伽马的探测范围约0.3 m,利用快速反演储层界面方法反演了水平位移20~165 m的储层界面,共选取了5个界面关键点(如图5中A、B、C、D、E,ea为绝对误差);对比利用电法、声波和密度测井等曲线综合反演出的最终真实界面位置 [8] [11] [13] ,可以看到利用快速反演储层界面方法得到的储层界面准确性高,最大绝对误差仅0.06 m (A点),平均绝对误差为0.03 m。考虑到地层横向上自然伽马特征的非均质性特点,误差分析结果表明快速反演储层界面方法可较为准确地反演储层界面,为实时地质导向工作提供参考。
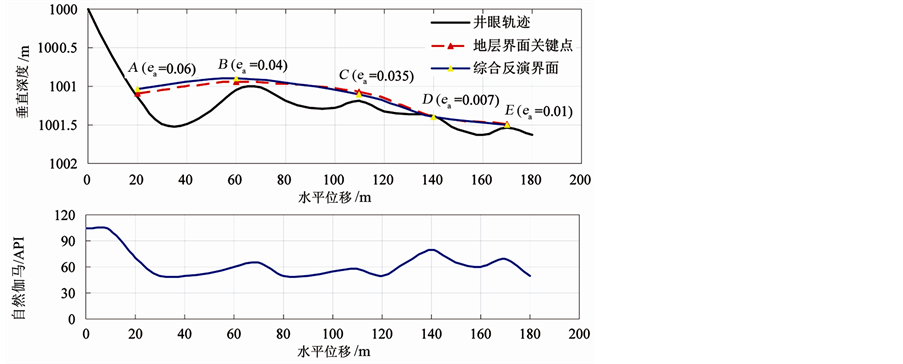
Figure 5. Schematic of the reservoir interface inversion using gamma ray logging in S Well
图5. S井随钻伽马测井反演储层界面示意图
5. 结论
1) 利用随钻伽马快速正演算法,建立了不同伽马特征地层的界面与随钻伽马测井响应之间的关系图版,在该基础之上,建立了适应不同自然伽马特征地层的随钻伽马测井快速反演储层界面的方法。
2) 在建立的理论地层界面模型中,快速反演储层界面方法计算的界面绝对误差仅0.01 m;在S井随钻伽马测井现场实例中,该方法计算界面的最大绝对误差仅0.06 m,平均绝对误差为0.03 m。理论和实际地层界面模型反演结果表明,该方法可获得快速、准确的地层界面信息,可为随钻伽马测井的实时地质导向提供界面参考信息。