1. 引言
科学与工程领域中的一些反问题可以归结为第一类Fredholm积分方程 [1] [2] 。例如,图像处理、信号识别、遥感技术等问题。因为第一类Fredholm积分方程是病态的,对舍入误差比较敏感,所以要采取正则化方法,才能得到稳定的近似解。正则化方法的理论比较成熟,也有比较多的研究成果,但是,数值计算方法还有很多问题可以研究,尤其是多尺度快速算法 [3] [4] [5] [6] [7] 。
多尺度快速算法是20世纪90年代发展起来的一种求解算子方程的快速算法, 其主要思想是首先构造具有紧支集和消失矩的多尺度基底来离散算子方程, 使所得离散化后的代数方程组的系数矩阵具有层次性和数值稀疏性。
2002年,Z. Chen, C. A. Micchelli和Y. Xu在文献 [3] 中提出求解第二类积分方程的快速配置法,建立了一套完整的理论框架。快速配置法改善了传统配置法的两大主要不足,一方面使得系数矩阵稀疏,另一方面降低了系数矩阵的条件数。
多尺度快速算法从适定问题到不适定问题有了一个飞跃。当解不适定问题进行参数选取时,需要大规模的运算,因此有必要发展多尺度快速算法。
2008年,Z. Chen, Y. Xu 和H. Yang在文献 [4] 中求解不适定积分方程时发展了多尺度快速配置法,给出了Banach空间范数意义下的误差估计,提出了一种先验参数估计和自适应后验参数选取策略,并证明了在这两种参数选取策略下所获得的近似解均具有最优收敛阶。但是,该方法为了得到最优收敛阶,要求精确解具有较高的光滑度。如果积分算子是扇形算子,那么,可以降低精确解的光滑度要求,也能够得到近似解的最优收敛阶。
Plato于1996年,在文献 [8] 提出了Banach空间求解扇形积分方程的正则化方法以及后验参数选择方法,给出了近似解的收敛率。缺点是无限维空间无法求出数值解。
因此,本文的主要工作是在有限维空间中给出求解积分方程的多尺度快速配置法。文中基于多尺度配置法给出矩阵压缩技术,减少系数矩阵非零元素的计算量,并提出自适应后验参数选择策略,确保近似解的最优收敛率。
2. 交替迭代法
设 是
是 中的一个紧集,扇形算子
中的一个紧集,扇形算子 ,定义为
,定义为

其中核函数 且算子
且算子 满足
满足
(H1) [8] 算子 的预解集
的预解集 包含某个扇形面,即
包含某个扇形面,即
 (2.1)
(2.1)
其中 。算子
。算子 的预解算子
的预解算子 有如下估计
有如下估计
 (2.2)
(2.2)
其中 是正常数。
是正常数。
考虑第一类Fredholm积分方程
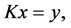 (2.3)
(2.3)
其中 是已知函数,
是已知函数, 是未知函数。若
是未知函数。若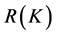 是非闭集,则方程(2.3)是一个病态问题。实际问题中,仅仅知道右端项
是非闭集,则方程(2.3)是一个病态问题。实际问题中,仅仅知道右端项 的近似值
的近似值 ,满足
,满足
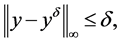 (2.4)
(2.4)
其中 。因此,实际求解的是如下的方程
。因此,实际求解的是如下的方程
 (2.5)
(2.5)
为了得到方程(2.5)的近似解,要采取正则化方法。以下采用文献 [8] 中的交替迭代法
 (2.6)
(2.6)
其中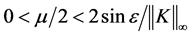 是松弛因子。
是松弛因子。
为方便起见,令

容易算得近似解 可表示为:
可表示为: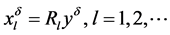 。
。
设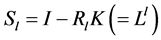 ,为了得到近似解的收敛性,需要以下引理。
,为了得到近似解的收敛性,需要以下引理。
引理2.1. [8] 若条件(H1)成立, ,则对任意
,则对任意 ,有
,有
 (2.7)
(2.7)
以及
 (2.8)
(2.8)
其中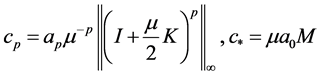 。
。
为了得到近似解的收敛率,要求方程(2.3)精确解 ,应满足如下的光滑性(见 [8] )。
,应满足如下的光滑性(见 [8] )。
(H2) 存在常数 ,使得精确解
,使得精确解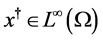 满足
满足

定理2.1. 若条件(H1)-(H2)成立,则
 (2.9)
(2.9)
证明:根据条件(H1), 和
和 的定义,有
的定义,有

由引理2.1和假设(H2),推得

3. 多尺度配置法
以下讨论有限维空间上求解交替迭代正则化方程(2.6)的配置法 [3] 。为此,给出一些符号。令 ,
, ,
, 。假设近似空间
。假设近似空间 是嵌套的,即
是嵌套的,即 。因此,
。因此, 可分解为
可分解为
 (3.1)
(3.1)
假设 ,对每个
,对每个 都有一组基
都有一组基 ,使得
,使得 ,假设
,假设 ,
, ,
,
假设配置泛函空间 ,满足 [5]
,满足 [5]
1) ,
,
2) ,
,
3) 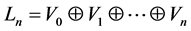
其中 表示线性泛函
表示线性泛函 在
在 上的取值。对
上的取值。对 ,
, 表示从
表示从 到
到 的插值投影,定义如下。设
的插值投影,定义如下。设 ,
, 满足
满足

假设 表示从
表示从 到
到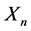 的正交投影。当离散层
的正交投影。当离散层 和迭代步
和迭代步 存在某种关系时,多尺度配置法求解方程(2.6),就是找
存在某种关系时,多尺度配置法求解方程(2.6),就是找 ,使得
,使得
 (3.2)
(3.2)
其中 。
。
在多尺度基函数和相应的配置泛函下,算子 是稠密矩阵,为此,采用如下的压缩算子
是稠密矩阵,为此,采用如下的压缩算子

其中 。用
。用 替代方程(3.2)中的
替代方程(3.2)中的 ,得到求解方程(2.6)的快速算法,即找
,得到求解方程(2.6)的快速算法,即找 使得
使得
 (3.3)
(3.3)
利用 的多尺度基函数,近似解
的多尺度基函数,近似解 可以表示为
可以表示为

为了写成矩阵形式,引入下面的记号。

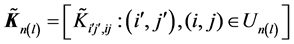
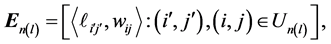
其中
 (3.4)
(3.4)
方程(3.3)的矩阵形式如下:
 (3.5)
(3.5)
其中, 。
。
对于截断算法的计算复杂度,引入文献 [5] 的结果即可。
引理3.1. [5] 若矩阵 是采用截断策略(3.4)所得,那么
是采用截断策略(3.4)所得,那么
 (3.6)
(3.6)
其中 表示求解式(3.5)中的
表示求解式(3.5)中的 所要计算的非零元素个数。
所要计算的非零元素个数。
4. 误差估计
为了分析多尺度配置法离散后的近似解误差估计,给出下面的假设 [4] 。
(H3) 对某些正常数 ,存在正常数
,存在正常数 ,使得
,使得
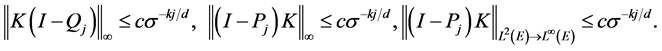
为了得到误差估计,先给出引理。
引理4.1. [4] 假设条件(H1)、(H3)成立,则存在常数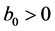 ,使得对任意的
,使得对任意的 ,
,
 (4.1)
(4.1)
其中 。
。
定理4.2. 假设条件(H1)、(H3)成立,且离散层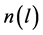 满足不等式
满足不等式
 (4.2)
(4.2)
则算子 可逆且,
可逆且,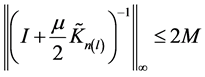 。
。
证明:由条件(H1)得 ,以及(4.1)和(4.2)推得
,以及(4.1)和(4.2)推得

又因为

所以 可逆且
可逆且

接下来估计误差 。由式(2.6)和(3.3)可知,
。由式(2.6)和(3.3)可知,


其中
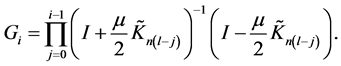
令

类似于文献 [9] ,有以下关系

其中 。
。
定理4.3. 若 ,条件(H1)-(H3)和式(2.4)成立,迭代步
,条件(H1)-(H3)和式(2.4)成立,迭代步 满足
满足 , 离散层
, 离散层 满足
满足
 (4.3)
(4.3)
则

其中 。
。
证明:将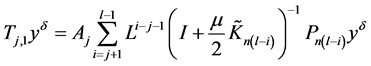 变形为
变形为 ,
,
其中,


由不等式(2.7)、(4.1)与(4.3),得

以及 ,得
,得

由

以及不等式(4.1),(4.3)条件(H3),得

其中 。因此,
。因此,
 ,
,
其中 。类似有
。类似有

同理,有

于是,

由 ,推得
,推得 。于是
。于是

其中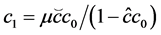 。记
。记

根据式(4.1)以及式(4.3)和条件(H3),得

于是,


定理4.4. 若 ,条件(H1)-(H3)成立,则
,条件(H1)-(H3)成立,则
 (4.4)
(4.4)
其中 。
。
证明:显然有

由定理4.3,推得

以及不等式(2.9),得

根据定理4.4,得到下面的先验参数选择策略。
定理4.5. 若条件(H1)-(H3)和式(2.4),(4.2)成立,取 ,则
,则
 (4.5)
(4.5)
证明:根据定理 4.4 和 ,
, 显然成立。
显然成立。
5. 自适应参数选择
这一节,给出迭代停止准则。根据上述分析可知,存在两个恒大于零的递减函数 和
和 ,使得
,使得
 (5.1)
(5.1)
其中 是满足不等式
是满足不等式 的最大正整数。这个结果表明,当
的最大正整数。这个结果表明,当 时(最优参数
时(最优参数 不一定是正整数)
不一定是正整数)

事实上,先验参数 很难实现。在实际应用中,通常给出正则化参数
很难实现。在实际应用中,通常给出正则化参数 的有限集合
的有限集合

其中 是某个正整数,
是某个正整数, 表示正整数集。集合
表示正整数集。集合 中的最佳参数记为
中的最佳参数记为

其中

如果函数 是未知的,那么上述的参数选择也是不可行的。对集合
是未知的,那么上述的参数选择也是不可行的。对集合 做进一步的分析,对任意的
做进一步的分析,对任意的 ,
,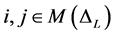 ,有
,有
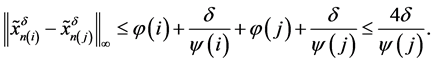
因此,用下面的集合

替代 ,并选择
,并选择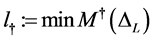 作为
作为 的近似值。
的近似值。
定理5.1. [10] 假设式(5.1)成立。若 ,且存在常数
,且存在常数 使得函数
使得函数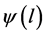 满足
满足
 (5.2)
(5.2)
则
 (5.3)
(5.3)
根据文献 [10] ,给出如下自适应参数选择方法。
算法5.2. (自适应参数算法)
1) 给出初值: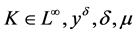 ;
;
2) 确定离散层 :满足
:满足

3) 取满足 的最大整数;
的最大整数;
4) 对于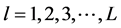 ,做如下迭代:
,做如下迭代:
a) 计算 ,满足下式:
,满足下式:

b) 取 。
。
定理5.3. 如果条件(H1)~(H3)成立, 是依据算法5.2选择,则
是依据算法5.2选择,则

证明:证明 满足定理5.1的所有条件。由定理4.4可知,
满足定理5.1的所有条件。由定理4.4可知,

取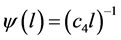 ,
,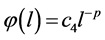 ,
, ,则对任意的
,则对任意的 ,
,
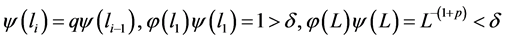
于是, 。这样就证明满足定理 5.1 的所有条件,故有
。这样就证明满足定理 5.1 的所有条件,故有

6. 数值算例
为了说明方法的有效性及理论结果的合理性,给出下面的数值实验结果。考虑下面的第一类积分方程

其中和为 [8]

为了检验数值结果,先给出右端精确函数

以及方程 的唯一精确解:
的唯一精确解: 。且
。且 (见 [8] ),此时
(见 [8] ),此时 。根据文献 [8] 引理1.2.7和1.2.8可知,上述的积分算子满足条件(H1),即
。根据文献 [8] 引理1.2.7和1.2.8可知,上述的积分算子满足条件(H1),即


为了说明在扰动的情况下,算法的有效性。假设右端扰动项 ,其中
,其中 且
且 ,其中
,其中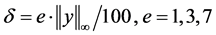 。取
。取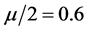 ,
, 。
。
下面介绍有限维空间 和配置泛函空间
和配置泛函空间 的构造。假设
的构造。假设 分解如下:
分解如下:

其中 是
是 上的分段线性多项式空间,对于
上的分段线性多项式空间,对于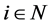 ,
, 是空间
是空间 在空间
在空间 中的正交补空间。现在给出在空间
中的正交补空间。现在给出在空间 满足条件的一组基底,并构造出空间
满足条件的一组基底,并构造出空间 中相应的基底,则空间
中相应的基底,则空间 的基底可以通过递归公式构造。选择空间
的基底可以通过递归公式构造。选择空间 的一组基底为
的一组基底为

空间 中相应的基底为
中相应的基底为

相应的递推公式为:


当 时,
时, ,
, 是
是 上的分段线性函数空间,节点为:
上的分段线性函数空间,节点为: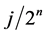 ,
, 。对应的配置泛函空间
。对应的配置泛函空间 有如下分解:
有如下分解: .对应的取
.对应的取 ,其中
,其中 ,
, 相应的有
相应的有 ,其中
,其中
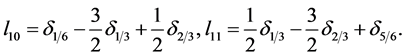
于是, 可以相应的得到. 有兴趣的读者可以参考文献 [3] 。在快速多尺度配置法下,得到了后验参数选择策略下的结果,见表1。由此可以看出算法是有效的。
可以相应的得到. 有兴趣的读者可以参考文献 [3] 。在快速多尺度配置法下,得到了后验参数选择策略下的结果,见表1。由此可以看出算法是有效的。
表1. 自适应误差估计
致谢
国家自然科学基金项目(11361005,61502107),江西省自然科学基金项目(20151BAB201011)。