1. 引言
粮食不仅是人们日常生活的必需食品，也是经济和社会发展的重要基础，具有不可小觑的重要作用 [1] 。一方面，随着人口增加、耕地减少、水资源短缺、气候变化、环境污染等问题日益突出，另一方面，来自国际方面粮食市场的竞争和冲击，导致中国粮食生产面临着相当大的挑战与风险。目前国内学者对粮食产量问题已经做了大量研究：何春花等 [2] 通过对河南省粮食产量分阶段分析得到粮食作物播种面积、化肥施用量和农林牧渔的总人数是贡献率位于前三的影响因素；史铁丑等 [3] 认为粮食的生产需要土地，中国人均耕地面积稀少不到世界人均耕地面积的一半，为了确保中国粮食安全，研究粮食作物播种面积及其影响因素有重要意义；王春娟等 [4] 认为影响粮食波动的最大因素为播种面积和粮食单产，及相关系列文献都提出研究粮食作物播种面积尤为重要。
根据国家“十三五”规划建议提出的“坚持最严格的耕地保护制度，坚守耕地红线，实施藏粮于地、藏粮于技”粮食战略。在国家重视耕地面积的同时，由于环境污染、贫富经济差加剧、城市化、工业化等原因，都会导致耕地面积的减少，因此，如何保证粮食作物播种面积的增加，充分地利用耕地面积显得十分必要，基于此研究我国粮食作物播种面积的影响因素，能够更加具体反应粮食作物播种面积变化。
目前粮食作物播种面积国内研究：陈婧 [5] 建立BP网络动态仿真模型,对黑龙江省未来粮食播种面积进行预测；丁立超 [6] 利用指数平滑法对粮食作物播种面积进行预测，得出未来几年内我国粮食作物播种面积将呈逐年增加趋势；马馨悦 [7] 认为最低价收购政策的实施和城乡收入差距对粮食种植面积有着至关重要的作用；周玲等 [8] 通过机器学习建模方法实证分析发现，影响我国粮食种植面积的主要因素有农业劳动力比重、农业机械总动力、农用化肥施用量等；赵红燕等 [9] 研究粮食最低收购价政策执行效果，对可能影响粮食种植面积的数个指标进行相关性分析，找出相关性系数较高的三个指标：第一产业就业人口、粮食净进口量、农机总功率；陈巧燕 [10] 等应用C-D生产函数模型和逐步多元回归分析法，表明粮食播种面积对粮食产量具有显著的正向作用；朱园等 [11] 利用协整分析和Granger因果检验对江苏省农作物播种面积与农业经济增长之间的长期均衡关系，认为江苏省粮食作物播种面积对农业总产值的增长起到很大作用。
据上述文献研究发现，影响粮食作物播种面积的因素有粮食净进口量、城乡收入比、农业机械总动力、化肥施用量、第一产业就业人口等。基于考虑影响因素的全面性，对前人的工作进一步拓展，本文首先增加了受灾面积和有效灌溉面积因素，以对环境问题和设备资源问题在粮食作物播种面积方面的影响进行探索，然后受部分学者 [10] [11] 提出的粮食播种面积对粮食产量和农业总产值有显著正向作用启发，考虑到上一年粮食产量和农业总产值对粮食播种面积的作用关系未知，本文继而增加了农业总产值和粮食产量，最后综合以上影响因素定量分析哪些因素对我国粮食作物播种面积影响显著，并据此对今后粮食播种面积的发展提出参考建议。
2. 数据分析
2.1. 数据来源及变量
本文所用数据来源于中华人民共和国国家统计局 [12] ，在其中国统计年鉴网页上查阅了从1996年到2016年间我国农业的部分数据，其余数据来源于中国农村统计年鉴。这些数据的名称分别为粮食作物播种面积(千公顷)、粮食净进口量(万吨)、城乡收入比、农业机械总动力(万千瓦)、受灾面积、第一产业就业人口、化肥施用量(万吨)、有效灌溉面积(千公顷)、农业总产值(亿元)、粮食产量(万吨)，各变量名称如表1所示。
2.2. 数据说明
1) 粮食净进口量：随着我国粮食缺口加大和粮食进口量的增加，我国已转变为粮食净进口国。因此,使用粮食净进口量来描述粮食进出口量情况，粮食净进口量 = 进口量 − 出口量。
2) 城乡收入比：改革开放以来，我国城乡居民收入差距不断增大，成为急需解决的社会问题。为了研究其对粮食种植面积的影响，引入城乡居民收入差距指数进行分析。城乡居民收入差距指数 = 城镇居民人均可支配收入/农村居民人均纯收入。
3) 第一产业就业人口数：农民是种植业的主体，农民数量的变化直接影响农业生产力的变化，因此，在考虑影响粮食种植面积时，我们将农业的劳动人口数量作为影响因素之一，为方便数据查询，用第一
Table 1. Explanatory note for each variable
表1. 各变量说明
产业就业人口数代替农村劳动力人口数。
4) 农业机械总动力：代表国内农业机械化程度。随着农业的发展，机械化逐渐取代人力耕种，生产力大大增加，在我国农业劳动人口逐年减少的情况下，机械化程度对保证粮食种植面积有着不可厚非的影响。
2.3. 数据标准化
数据标准化是统计学上常用的方法，本文的数据处理方法是标准差标准化，这种方法基于原始数据的均值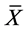
和方差
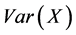进行数据的标准化。对变量进行的标准差标准化可以消除量纲(单位)影响和变量自身变异的影响。本文所使用的样本数据都通过Matlab软件首先进行了标准差标准化处理。
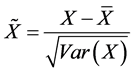
2.4. 变量相关系数
相关系数的大小，可以初步判断模型回归线性的强弱，现给出相关系数公式：
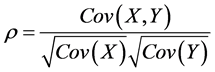
相关系数的大小表示相关系数的相关程度不一样：
1) 若
，称为完全正相关，
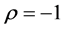称为完全负相关；
2) 若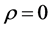
，表示没有线性关系；
3) 若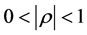
，则称有“一定程度”的线性关系，
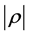越接近于1，则线性相关程度越高，越接近于0，则线性相关程度越低。
本文使用Matlab软件对变量之间的相关系数进行了计算，结果如表2所示。
2.5. 数据初步分析
从样本的相关系数表可以看出粮食作物播种面积与粮食产量、城乡收入比、农业总产值、第一产业就业人口，粮食净进口量有较强的线性相关性。接下来使用Matlab软件对样本数据进行回归，来更详细的说明粮食作物播种面积与九个自变量之间的关系。
3. 模型构建
回归分析是多元统计分析方法中应用最广泛的一种，它用于分析事物之间的统计关系，着重考察变量之间的数量变化规律，并通过回归方程的形式描述和反映这种关系，帮助人们准确把握变量受其他一个或多个变量影响的程度，进而为控制和预测提供科学依据，在解决实际问题时，我们通常从最简单而又最普遍的多元线性回归模型入手。
3.1. 多元线性回归
根据上述问题，中国粮食作物播种面积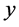
的影响因素有粮食净进口量(
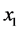)、城乡收入比(
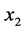)、农业机械总动力(
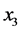)、受灾面积(
)、第一产业就业人口(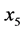
)、化肥施用量(
)、有效灌溉面积(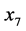
)、农业总产值(
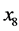)、粮食产量(
)。
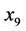多元线性回归模型 [13] 的基本形式：
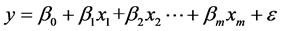
Table 2. Correlations between samples
表2. 样本间相关系数
其中，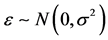
，
，
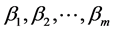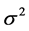都是未知参数，
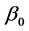称为回归常数，
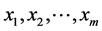为回归变量，
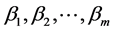为回归系数。
假设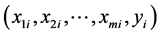
，
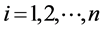，是
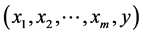的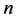
个观测值，则它们满足关系
，
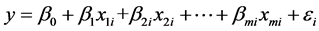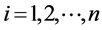
式中，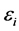
相互独立，则
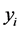也相互独立，且
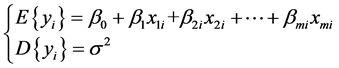
建立多元线性回归模型，首先要估计未知参数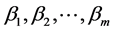
，为此得到
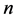组数据
，
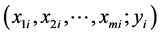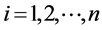
则有：
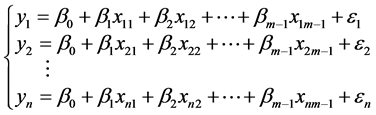
其中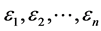
相互独立，且服从
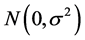分布。令
，
，
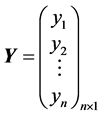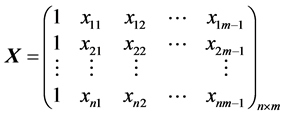
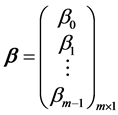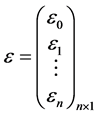
写成矩阵形式为：
式中，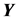
称为观测向量，
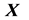称为设计矩阵，它们是由观测数据得到的，是已知的，
是待估计的未知参数向量，
是由不可观测的随机误差得到的，并简记为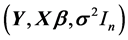
。
常常采用最小二乘法寻找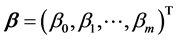
的估计值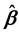
，
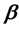的真值应该使误差向量
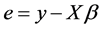达到最小，也就是它的长度平方达到最小
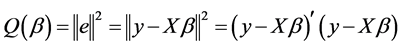
因此，我们应该通过求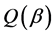
的最小值来求
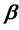的估计：
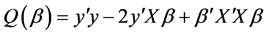
利用矩阵微商公式求解，则有：
，
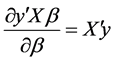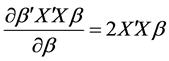
于是
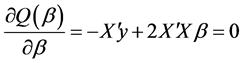
得到
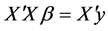
因为设计阵
满足
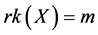，则有：
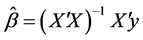
据模型建立，可以将标准化后样本数据代入公式求解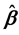
，本文使用的是Matlab软件 [14] ，求得结果如表3。
Table 3. Coefficients of the regression model, confidence interval of coefficients
表3. 回归模型的系数、系数置信区间
经整理后得到如下多元线性回归方程模型1：
模型1的拟合优度为0.9856，其调整拟合优度为0.9726，说明模型拟合数据的效果非常好,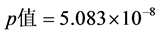
，表明回归方程高度显著，说明粮食作物播种面积和自变量有高度的线性关系。然后检验其回归系数的显著性。
在0.05的显著性水平下，有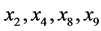
显著外，其他自变量都不十分显著，可能的原因是自变量之间存在多重共线性，回归系数通不过显著性检验，甚至给模型回归系数得不到合理的解释，另外我们通过绘制其残差图如图1，可以看到：除第8个点外，其余点偏离不是很大，说明模型1与原数据拟合效果比较理想。
3.2. 调整模型
在多元线性回归模型中可能遇到某个检验水平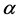
下，整个回归模型的统计检验小于
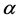，而模型的各偏回归系数的检验却大于
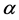，根据数据的专业知识，已知模型的因变量与自变量之间有重要的联系，但检验结果大于
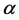，在统计学中这种现象称为多重共线性。当自变量之间存在近似的线性关系，即某个自变量能由其它自变量的线性组合表示时，就会造成参数估计的误差急剧增大，这会对回归分析产生严重的影响，为此在建模前需要消除变量之间的多重共线性。消除多重共线性的方法有很多，例如主成分回归法、逐步回归法、岭回归法、偏最小二乘回归法等，本文主要采用逐步回归法来进一步综合分析粮食作物播种面积的影响因素。
3.3. 逐步回归法
逐步回归法是线性回归分析中重要的一种分析方法，主要用来解决多元线性回归模型中解释变量个数较多时，如何筛选解释变量以使得回归模型中包含所有对被解释变量影响显著的解释变量而不包含影响不显著的解释变量的问题。它的主要思路是将全部解释变量中按对被解释变量的贡献大小逐个引入回归方程，已被引入回归方程的变量在引入新变量后也可能失去显著性，而需要从回归方程中剔除出去。引入一个变量或者从回归方程中剔除一个变量都要进行F检验，同样对已经选入的解释变量逐个进行t
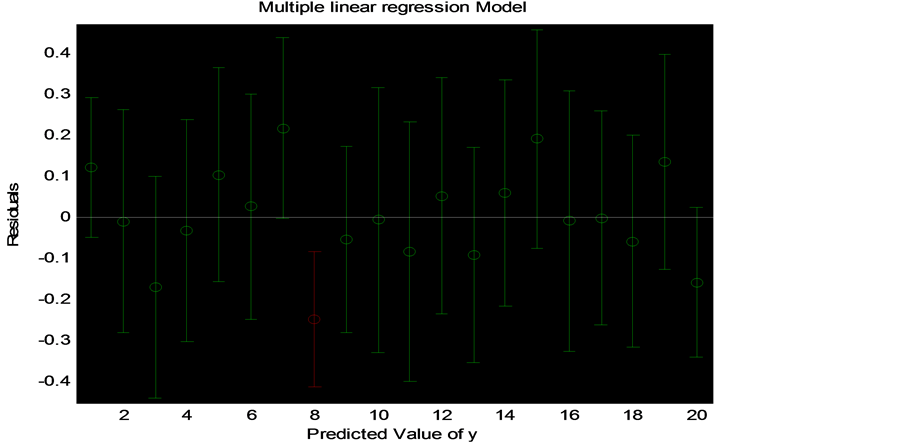
Figure 1. Residual plot: result of model 1
图1. 模型1的残差图
检验，以确保每次引入新的变量之前回归方程中只包含显著性变量。这是一个反复的过程，直到既没有显著的解释变量选入回归方程，也没有不显著的解释变量从回归方程中剔除为止，以保证最后所得到的解释变量集是最优的。
通过用Matlab软件 [15] 求解逐步回归法，我们可以得出如下三个模型：
在上面用线性回归法得到的模型1中，自变量存在多重共线性，对其系数做回归系数检验表4，在0.05的显著性水平下，回归系数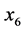
最不显著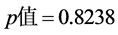
，首先剔除化肥施用量(
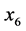)，其余变量进行回归。得到模型2的回归方程为：
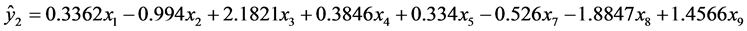
可以知道模型2的拟合优度为0.9855，其调整拟合优度为0.9750，继续对其系数做回归系数检验表5，回归系数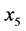
不显著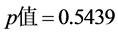
，所以剔除第一产业就业人口(
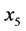)，得到模型3的回归方程为：
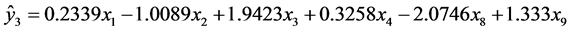
可以知道模型3的拟合优度为0.9850，其调整拟合优度为0.9762，将剩下的变量进行回归系数检验表6，得到回归系数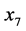
不显著
，所以剔除有效灌溉面积(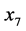
)，最后得到模型4的回归方程为：
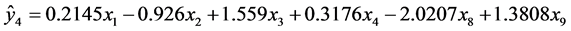
可以知道模型4的拟合优度为0.9846，其调整拟合优度为0.9775，调整拟合优度值越大，说明模型越好，在模型4的方程中，继续剔除变量，都没有模型4的调整拟合优度好，所以最终可以确认模型4为最佳模型。由模型4可以知道在其他条件不变的情况下，每增加一单位农业机械总动力(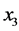
)，粮食作物播种面积增加1.559个单位，粮食净进口量(
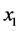)每增加一单位，粮食作物播种面积增加0.2145个单位，城乡收入比(
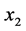)每增加一单位，粮食作物播种面积减少0.926个单位，受灾面积(
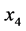)每增加一个单位，粮食作物播种面积增加0.3176个单位。农业总产值(
)每增加一单位，粮食作物播种面积减少2.0207个单位。粮食产量(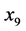
)，每增加一单位，粮食作物播种面积增加1.3808个单位。
Table 4. Regression coefficients test results of model 1
表4. 模型1回归系数检验结果
Table 5. Regression coefficients test results of model 2
表5. 模型2回归系数检验结果
Table 6. Regression coefficients test results of model 3
表6. 模型3回归系数检验结果
4. 结论与建议
4.1. 结论
本文基于多元线性回归法、逐步回归法对粮食作物播种面积影响因素进行分析，通过所建立的最佳模型4及其调整拟合优度为0.9775，得出结论：
1) 对粮食播种面积贡献最为明显的是农业机械总动力，其次分别粮食产量、城乡收入比、受灾面积，影响最大的是农业总产值，影响最小的是粮食净进口量。
2) 有效灌溉面积、第一产业就业人口、化肥施用量不能有效影响粮食作物播种面积。
3) 农业机械总动力、受灾面积、粮食净进口量、粮食产量对粮食作物播种面积有促进作用，城乡收入比、农业总产值对粮食作物播种面积有抑制作用。
4.2. 建议
随着我国城市经济的快速发展，城乡收入比逐年加大，农民缺乏粮食种植的动力和信心，导致粮食作物面积减少，建议国家出台更多惠农政策，使得农民从中获利，增加种粮的积极性。粮食受灾面积的增加，导致单位面积内的粮食产量的减少，国家可以在一定程度上去治理受灾耕地，从而促进粮食作物播种面积的增加。进一步的机械化程度加深，会让农民生产效率得到显著提高，有利于农民种植播种面积的扩大，因此，国家在制定相关政策时要加快研发机械技术步伐，尽可能加大机械在农村的普及力度，这与我国制定的“十三五”规划中实施“藏粮于地、藏粮于技”粮食战略相一致。