1. 引言
一个简单的生命,也包含庞大的数据信息,数据构成十分复杂。随着生物科技的蓬勃发展,与生物有关的统计研究逐步展开,生物学数据的处理与分析成为一个重要的研究领域。有时我们获得的生物学样本数据不完整,导致研究工作困难重重。如何填补缺失的数据,也就成为了一个亟待解决的问题。
在生物样本数据中,通常情况下缺失的数据无非两种:属性值和分类值。如果缺失了属性值,可以进行回归填补;如果缺失了类别值,可以进行分类填补。这些都可以用支持向量机实现。就支持向量机而言,分类问题和回归问题都是根据训练样本找到一个实值函数g(x):回归问题就是给定一个新的模式,根据训练样本确定一个实值函数g(x),使用y = g(x)推断任一输入x所对应的输出y (实数);分类问题就是给定一个新的模式,根据训练样本找到一个实值函数g(x),使用y = sign(g(x))推断任一输入x所对应的类别(如:+1,−1) [1] 。文献 [2] 使用RBF神经网络对上证指数进行预测,类似地,填补缺失的属性值也可以用人工神经网络回归预测进行处理。本文从R内置数据集iris中按需要选取样本数据建立学习样本,模拟生物样本属性值缺失和类别缺失两种缺失数据的情况,以MATLAB为工具,采取支持向量机和人工神经网络的模型,以无缺失值的样本预测有缺失值的样本中的缺失值,从而进行填补。属性值缺失值用支持向量机或人工神经网络进行回归填补,样本类别缺失值用支持向量机分类填补。神经网络推导出的各种算法很难在样本数据有限时取得理想的应用效果,需要设计者有效利用自己的经验。与神经网络相比,支持向量机能够基于有限的样本信息求解,同时避免了神经网络实现中的经验成分。
2. 填补缺失的样本属性值
2.1. 支持向量机回归填补
支持向量机SVM (Support Vector Machines)是由Vanpik领导的AT&TBell实验室研究小组在1963年提出的一种新的分类技术,在解决小样本、非线性、高维模式识别问题中表现出许多特有的优势,并且可以推广应用到函数拟合等问题中去 [3] 。
我们从R语言内置的iris数据集中的setosa类别选取20个样本组成一个新的数据集,作为网络学习样本,并删去第二十个样本的最后一个属性值(Petal.Width),模拟数据缺失的情况,如表1。其实,无论缺失的是什么位置的数据,只要将没有缺失数据的行列集合到一起,作为训练集,用来预测数据不完全样本的缺失属性的值。选取1到19个样本的Sepal.Length、Sepal.Width、Petal.Length、Petal.Width为自变量,2到20个样本的Petal.Width为因变量。
SVM的实现使用MATLAB的libsvm工具箱,实现数据归一化预处理,寻找回归的最佳参数,参数选择结果图(等高线图)如图1。用找到的最佳参数对SVM进行训练,再对原始数据进行回归预测,得回归预测数据与原始数据对比图,如图2。SVM回归预测的均方误差MSE = 0.0312355,相关系数R = 67.5382%,缺失值填补为0.2969。
2.2. 人工神经网络回归填补
人工神经网络(Artificial Neutral Network, ANN)是由神经元相互连接,通过模拟人脑神经处理信息的方式,进行信息并行处理和非线性转换的复杂网络系统,在控制与优化、预测与管理、模式识别与图像处理、通信等方面得到了十分广泛的应用 [4] 。前向反馈(Back Programming, BP)网络和径向基(Radical Basis Function, RBF)网络是目前应用最广泛的两种网络。

Table 1. A set of biological samples with missing attribute values
表1. 有缺失属性值的生物样本集
注:20号样本缺失的Petal.Width真实值为0.3。

Figure 1. Parameter selection results (contour map)
图1. 参数选择结果图(等高线图)
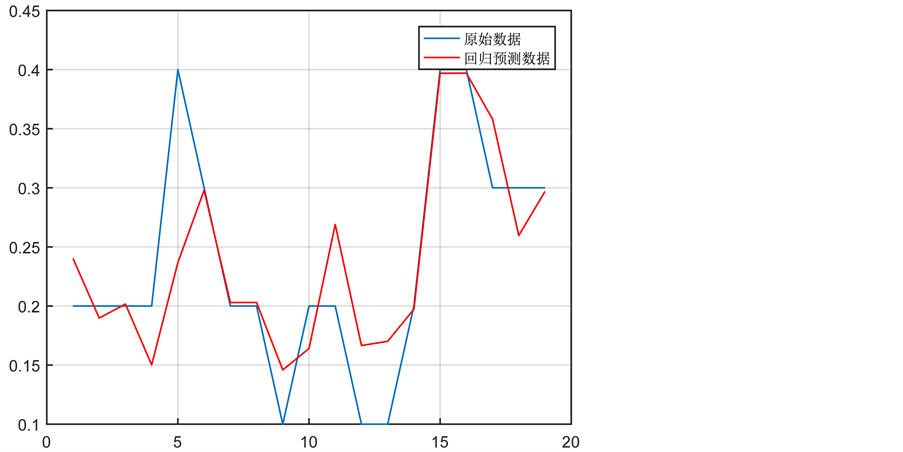
Figure 2. Regression prediction data and the original data comparison chart
图2. 回归预测数据与原始数据对比图
2.2.1. BP神经网络填补
BP神经网络是一种具有三层或者三层以上神经元的神经网络,包括输入层、中间层(隐含层)和输出层,上下层之间全连接,而同一层的神经元之间无连接,两个神经元之间的连接强度为网络的权值。BP算法称为“误差反向传播算法”,通过误差逆向传播修正的反复进行,逐步修正各连接权值,核心是“负梯度下降”理论,误差调整方向沿着误差下降最快的方向进行 [5] 。
使用表1数据为网络学习样本。在本例中将前三个属性作为输入,Petal.Width作为输出,构成3个输入1个输出的网络,将前19个无缺样本数据作为训练样本集,后1个有缺样本作为预测检验样本。
对样本的输入、输出数据进行规格化处理: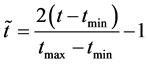 ,其中,
,其中, 和
和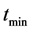 分别为
分别为 的最大值和
的最大值和
最小值, 为规格化后的变量。MATLAB中提供了对数据进行规格化处理的函数[tn,pn] = mapminmax(t),相应的逆处理函数t = mapminmax(‘reverse’,tn,ps),执行的算法是
为规格化后的变量。MATLAB中提供了对数据进行规格化处理的函数[tn,pn] = mapminmax(t),相应的逆处理函数t = mapminmax(‘reverse’,tn,ps),执行的算法是 [6] 。
[6] 。
BP网络用于函数逼近时,权值的调节采用的是负梯度下降法,这种调节权值的方法存在收敛速度慢和局部极小等缺点。
BP网络的学习过程常发生振动,每一次运行的结果可能会相差很大。如果将隐含神经元个数取为3,查看某一次运行结果的回归结果图(图3)和误差直方图(图4),可以得知,此时数据拟合的不好,误差也相当大。
对于隐含层的神经元个数的确定,至今尚未找到一个很好的解析式,只能根据经验确定或自行设计一些估计方法 [7] 。在初始化神经网络时,为了使计算结果相对稳定,往往需要进行多次实验,从而找到使结果最稳定的隐含层神经元个数。
2.2.2. RBF神经网络填补
RBF神经网络是模拟视网膜的感受功能产生的:距离感受视野中心越近的视神经元越兴奋;视神经元的激活区域呈径向对称。将视网膜感受原理映射到RBF神经网络,可对隐含层神经元进行建模:
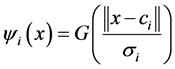 。其中,
。其中,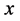 为输入样本;
为输入样本; 为感受视野中心(中心点),决定了径向基函数围绕中心点
为感受视野中心(中心点),决定了径向基函数围绕中心点
的宽度;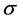 为宽度;
为宽度;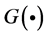 为径向基函数,也称激励函数、传递函数或激活函数;
为径向基函数,也称激励函数、传递函数或激活函数;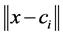 是距离函数,表示网络样本值与数据中心(中心点)之间的距离;
是距离函数,表示网络样本值与数据中心(中心点)之间的距离;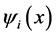 为网络输出。隐含层神经元径向基函数通常选用
为网络输出。隐含层神经元径向基函数通常选用
Gaussian函数,则上述神经元相应模型转化成: [4] 。
[4] 。
RBF网络也有三层,隐含层激活函数是高斯函数,第一层(输入神经元)和第三层(输出神经元)一般采用线性激励函数;依据链式偏微分法则,可得网络数据中心、宽度和权值的调整量 [8] 。利用MATLAB提供的神经网络工具箱 [9] 实现人工神经网络的功能十分方便。RBF与BP的不同点在于,中间隐含层神经元的个数,BP网络需要根据经验取定,RBF网络会在训练过程中自适应地取定。依然使用表1数据作为网络学习样本,RBF网络预测第20个样本的缺失属性值(Petal.Width)为0.2489,相对误差为17.02%。可见,RBF网络模型的预测结果优于BP网络模型的预测结果。
3. 填补缺失的样本类别
选取iris数据集中setosa、versicolor的样本各10个,组成一个新的数据集。删去新数据集中10号和20号样本的类别,模拟类别值缺失的情况,如表2。令setosa、versicolor为“1”类、“2”类,那么缺失的10号和20号样本的类别真实值分别为“1”和“2”。
用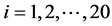 分别表示20个样本,第i个样本的第j个属性取值为
分别表示20个样本,第i个样本的第j个属性取值为 。类别已知的18个样本点的
。类别已知的18个样本点的
均值向量 ,标准差向量
,标准差向量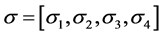 。对所有样本点数据进行标准化处理:
。对所有样本点数据进行标准化处理: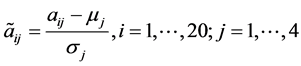 。对应地,称
。对应地,称 为标准化指标向量。记
为标准化指标向量。记 。记标准化后的18个类别已知的样本点数据行向量为
。记标准化后的18个类别已知的样本点数据行向量为 。利用线性内核函数的支持向量机模型进行分类,求得支持向量:
。利用线性内核函数的支持向量机模型进行分类,求得支持向量: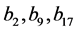 ,线性分类函数:
,线性分类函数: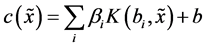 ,其中
,其中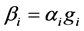 ,
, ,
, 。当
。当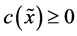 时,
时,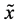 属于“1”类;当
属于“1”类;当 时,
时, 属
属
于“2”类 [6] 。

Table 2. A set of biological samples with missing category values
表2. 有缺失类别值的生物样本集
注:10号、70号样本缺失的类别真实值分别为setosa、versicolor。
用判别函数判别,得到缺失的第十个、第二十个样本类别分别为“1”、“2”,与真实值一致。所有已知样本点回代分类函数皆正确,误判率为0。
4. 缺失数据填补效果比较与分析
因为神经网络基于传统统计学,研究样本无穷大时的渐进理论 [10] ,故以此推导出的各种算法很难在样本数据有限时取得理想的应用效果。同时,因为神经网络是基于经验的风险最小化,不能保证网络的泛化能力 [11] ,故需要设计者有效利用自己的经验,网络系统的优劣是因人而异的。
与神经网络相比,支持向量机以统计学理论为基础,主要针对小样本情况 [12] ,能够基于有限的样本信息求解。同时,支持向量机基于结构风险最小化原则,有严格的理论和数学基础 [13] ,可以避免神经网络实现中的经验成分。
致谢
大学生创新创业项目(X201610022132)对全基因组关联分析中数据缺失研究。