1. 引言
互连网络是超级计算机的重要组成部分。互连网络可以模型化为一个图。图的顶点表示系统中的处理机,图的边表示处理机之间的通信链路,其中有向边表示单工通信链路,无向边表示半双工通信链路 [1] 。该文中讨论的是无向图。各种已有互连网络参见 [1] - [15] 。广义b-基超立方体网络是一种特殊的凯莱图,由Lakshmivarahan和Dhall [2] 中提出,因广义b-基超立方体网络有简单对称正则的结构而被研究。广义b-基超立方体网络是超立方体网络的推广,在很多性质方面优于超立方体网络,例如直径,连通性,容错直径等 [3] 。
图的控制理论是图论的重要分支,美国图论学者W. T. Haynes等 [16] 在1998年出版的专著较为系统地综述了这一领域的一些重要研究成果。尤其在图的点控制方面,提出了多种控制概念。事实上,我们在研究网络的各种控制数时,总是将该网络的一些基本参数(如顶点数,度,直径等)相联系。该文其余结构如下,第二节,给出相关的定义;第三节,给出当 时广义b-基超立方体网络控制数的具体值,以及当
时广义b-基超立方体网络控制数的具体值,以及当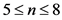 时控制数的界,进一步提出了两个问题和两个猜想;第四节,结束语。
时控制数的界,进一步提出了两个问题和两个猜想;第四节,结束语。
2. 预备知识
定义1 [17] :设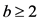 ,
,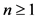 ,其中
,其中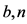 都是整数。定义
都是整数。定义
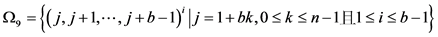

 表示由
表示由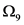 生成的凯莱图,并且
生成的凯莱图,并且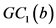 同构于
同构于 ,
,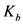 是具有
是具有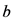 个顶点的完全图。在这里“
个顶点的完全图。在这里“ ”表示标准的笛卡尔积运算。
”表示标准的笛卡尔积运算。
显然,广义b-基超立方体网络是2元超立方体的一种推广。
定义
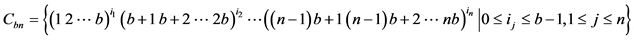
置换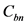 的子群由
的子群由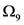 生成。
生成。
设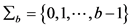 ,定义一个编码
,定义一个编码
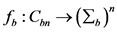
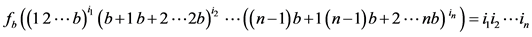
因此,我们将 表示为
表示为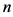 维b-基超立方体。
维b-基超立方体。
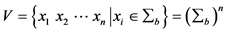
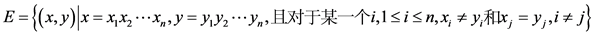
 的主要性质:
的主要性质:
1)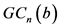 是
是 正则的,有
正则的,有 个顶点和
个顶点和 条边。
条边。
2) 直径为
直径为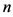 。
。
3) 是距离可迁的,因而是顶点可迁,且是对称的,距离正则的。
是距离可迁的,因而是顶点可迁,且是对称的,距离正则的。
定义2 [18] :设 为一个图,
为一个图, 如果对于每个点
如果对于每个点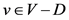 ,存在
,存在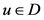 ,使得
,使得 ,则称
,则称 为
为 的一个控制集。图
的一个控制集。图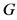 的控制数
的控制数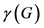 定义为:
定义为: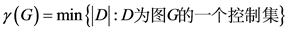 。
。
3. 广义b-基 超立方体网络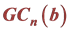 的控制数
的控制数
当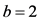 时,
时, ,
, 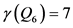 ,
, 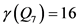 [19] 。
[19] 。
当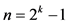 和
和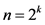 时,
时,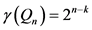 [20] 。
[20] 。
定理1:当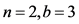 时,
时,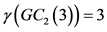 。其中
。其中 是
是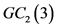 的控制数。
的控制数。
证明:当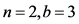 时,
时,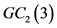 见图1,取
见图1,取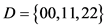 。即
。即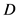 为
为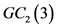 的控制集,且
的控制集,且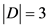 。
。
为了证明以下定理,我们给出以下记号。
我们用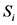 表示顶点坐标第1个位置为
表示顶点坐标第1个位置为 的所有顶点的集合,
的所有顶点的集合, 。
。
定理2:当 时,
时,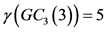 。其中
。其中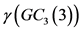 是
是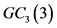 的控制数。
的控制数。
证明:当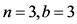 时,
时,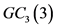 见图2,取
见图2,取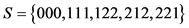 是
是 的控制集。因此
的控制集。因此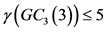 。现在,令
。现在,令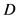 是
是 的任意一个控制集。我们断言
的任意一个控制集。我们断言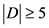 ,我们考虑以下情况。
,我们考虑以下情况。
情况1: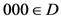
若 ,那么
,那么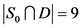 ,即
,即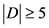 。
。
若 而
而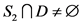 ,那么
,那么 。如果
。如果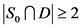 ,那么
,那么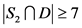 ,即
,即 。如果
。如果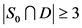 ,那么
,那么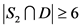 ,即
,即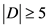 。如果
。如果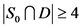 ,那么
,那么 ,即
,即 。如果
。如果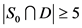 ,那么
,那么 ,即
,即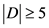 。如果
。如果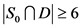 ,那么
,那么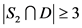 ,即
,即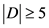 。如果
。如果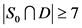 ,那么
,那么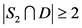 ,即
,即 。如果
。如果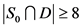 ,那么
,那么 ,即
,即 。如果
。如果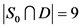 ,那么
,那么 ,即
,即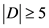 。以上情况
。以上情况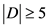 。
。
若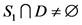 而
而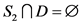 ,证明过程和
,证明过程和 而
而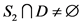 类似。
类似。
情况2: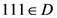
根据对称性,证明跟 情况1类似。
情况3: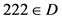
根据对称性,证明跟 情况1类似。
情况4: ,
,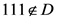
若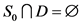 ,那么
,那么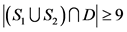 。如果
。如果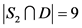 ,那么
,那么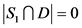 ,即
,即 。如果
。如果 ,那么
,那么 ,即
,即 。如果
。如果 ,那么
,那么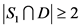 ,即
,即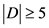 。如果
。如果 ,那么
,那么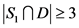 ,即
,即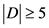 。如果
。如果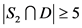 ,那么
,那么 ,即
,即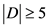 。如果
。如果 ,那么
,那么 ,即
,即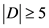 。如果
。如果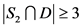 ,那么
,那么 ,即
,即 。如果
。如果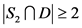 ,那么
,那么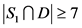 ,即
,即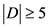 。如果
。如果 ,那么
,那么 ,即
,即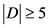 。以上情况
。以上情况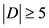 。
。
若 ,证明过程和
,证明过程和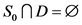 类似。
类似。
若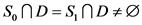 ,那么
,那么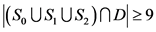 。如果
。如果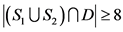 ,那么
,那么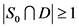 ,即
,即 。如果
。如果 ,那么
,那么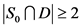 ,即
,即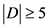 。如果
。如果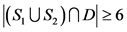 ,那么
,那么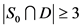 ,即
,即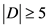 。如果
。如果 ,那么
,那么 ,即
,即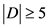 。如果
。如果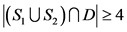 ,那么
,那么 ,即
,即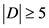 。如果
。如果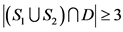 ,那么
,那么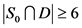 ,即
,即 。如果
。如果 ,那么
,那么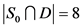 ,即
,即 。以上情况
。以上情况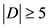 。
。
情况5: ,
,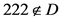
根据对称性,证明跟 情况4类似。
情况6: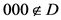 ,
,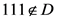 ,
,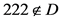 。
。
若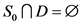 ,那么
,那么 。如果
。如果 ,那么
,那么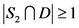 ,即
,即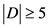 。如果
。如果 ,那么
,那么 ,即
,即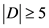 。如果
。如果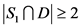 ,那么
,那么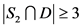 ,即
,即 。如果
。如果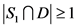 ,那么
,那么 ,即
,即 。以上情况
。以上情况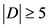 。
。
若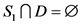 ,那么
,那么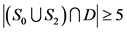 ,情况跟
,情况跟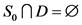 的类似,即
的类似,即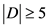 。
。
若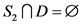 ,那么
,那么 ,情况跟
,情况跟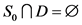 的类似,即
的类似,即 。
。
若 ,那么
,那么 ,即
,即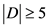 。
。
因此在所有的情况下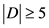 。
。
所以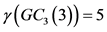 。
。
定理3:当 时,
时,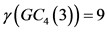 。其中
。其中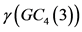 是
是 的控制数。
的控制数。
由于图过于复杂,我们在此给出顶点
0000, 0001, 0002, 0010, 0011, 0012, 0020, 0021, 0022
0100, 0101, 0102, 0110, 0111, 0112, 0120, 0121, 0122
0200, 0201, 0202, 0210, 0211, 0212, 0220, 0221, 0222
1000, 1001, 1002, 1010, 1011, 1012, 1020, 1021, 1022
1100, 1101, 1102, 1110, 1111, 1112, 1120, 1121, 1122
1200, 1201, 1202, 1210, 1211, 1212, 1220, 1221, 1222
2000, 2001, 2002, 2010, 2011, 2012, 2020, 2021, 2022
2100, 2101, 2102, 2110, 2111, 2112, 2120, 2121, 2122
2200, 2201, 2202, 2210, 2211, 2212, 2220, 2221, 2222
证明 是
是 的控制集。因此
的控制集。因此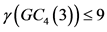 。可以根据定理2的过程来证明
。可以根据定理2的过程来证明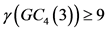 。所以
。所以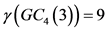 。
。
为了得出以下定理,我们给出如下引理:
引理1 [3] :对任意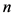 阶图
阶图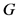 ,若
,若 为图
为图 的最大度,则有
的最大度,则有
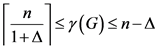
由以上引理我们可以推出:
推论1:图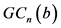 阶为
阶为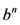 且度为
且度为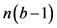 ,则有
,则有
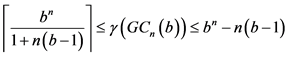
但是以上推论中得出的控制数的界范围过大,从而我们进一步细化,得出以下定理:
定理4:当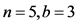 时,图
时,图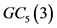 阶为
阶为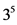 且度为10,则有
且度为10,则有
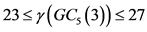
证明:令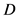 是图
是图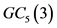 的最小控制集,图中每个顶点最多可以控制它自己以及另外10个点,所以
的最小控制集,图中每个顶点最多可以控制它自己以及另外10个点,所以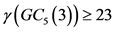 。若S = {00000, 00111, 00222, 01012, 01120, 01201, 02021, 02102, 02210, 10000, 10111, 10222, 11012, 11120, 11201, 12021, 12102, 12210, 20000, 20111, 20222, 21012, 21120, 21201, 22021, 22102, 22210}是
。若S = {00000, 00111, 00222, 01012, 01120, 01201, 02021, 02102, 02210, 10000, 10111, 10222, 11012, 11120, 11201, 12021, 12102, 12210, 20000, 20111, 20222, 21012, 21120, 21201, 22021, 22102, 22210}是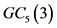 控制集。因此
控制集。因此 。即
。即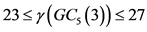 。
。
定理5:当 时,图
时,图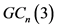 的阶为
的阶为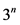 且度为
且度为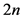 ,则有
,则有
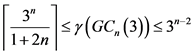
证明:根据定理4得证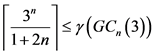 。
。
下证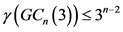 。因为
。因为 ,所以有
,所以有
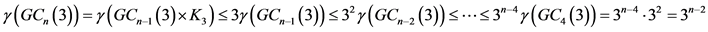
即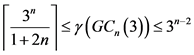 。
。
问题1:广义3-基n-立方体的控制数是多少?
猜想1:若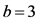 ,
,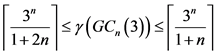 ,其中
,其中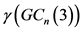 是广义3-基n-立方体
是广义3-基n-立方体 的控制数。
的控制数。
更一般地,我们有
问题2:广义b-基n-立方体的控制数是多少?
猜想2: ,其中
,其中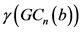 是广义b-基n-立方体
是广义b-基n-立方体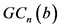 的控制数。
的控制数。
4. 结束语
广义b-基超立方体网络是一种非常重要的互连网络,通过分析与研究,给出了低维的控制数,以及其他维的控制数的界,但是广义b-基超立方体网络的很多其他性质还有待于研究。