基于瞬时无功功率理论的改进谐波检测APF设计

The Design of a Improved Harmonic Detection Method APF Based on Instantaneous Reactive Power Theory

摘要: 由于电网中大量电力电子器件的应用，导致电网中谐波问题严重。解决电网谐波问题，首先是对电网中谐波成分的检测，将三相三线制的电力系统中瞬时无功理论的基本原理，推广到三相四线制系统，验证在存在零序电流的情况下，低压配电网系统对检测负载电流谐波含量的实用性。在检测谐波含量的过程中，为有效解决传统方法中跟踪精度和响应速度无法兼备的问题，利用引入电流平均值法模块来代替传统LPF模块。通过Matlab搭建仿真模型，分析优化后算法的适用性及其高效性能。证明改进后的方法可以有效的解决精度和响应速度之间的问题，更有效的完成对谐波电流的检测，从而计算出指令电流，以便于实现对电网电流的补偿。

Abstract: Due to the application of a large number of power electronic devices in the grid, the harmonics problem is serious. The first to solve the harmonics problem is detection of harmonic components in power grid. The basic principle of the instantaneous power system of three-phase-three-wire system in reactive power theory is extended to three-phase-four-wire system by examining the practicability for harmonic detection in low voltage distribution network system with zero sequence current. In the process, for solving a tradeoff between maladjustment and the speed of dynamic response in the conventional detection method, the low-pass filter is substituted by current average method. By using the platform of Matlab to prove its applicability and highly active ability, it aims to prove that the improved method can resolve problems between accuracy and response speed and be more efficient detection of current harmonics. Thus we can calculate the referential current to complete the compensation of grid current.

1. 引言

随着科学技术的不断发展，应用到电力网络中的电力电子器件越来越普遍。供电网络中的非线性负载大量存在，使得电网的电压电流不再是原来的正弦波，而是畸变成含有谐波的电压电流波形，因此如何快速检测电流畸变程度的课题引发广泛关注 [1] 。现在普遍应用的谐波检测方法有快速傅里叶变换法FFT、离散傅里叶变换法DFT、神经网络法、FBD、瞬时无功理论等方法 [2] [3] ，瞬时无功理论因计算量小、动态响应迅速等特点而被普遍使用。由于目前低压配电网系统中低压配电端多采用三相四线制 [4] ，因此三线制有源电力滤波器APF [5] 已经无法满足系统检测的需求。基于以上分析，本文主要针对有源电力滤波器APF对谐波的检测和电流补偿的重要作用。

2. 瞬时无功理论的应用及推广

2.1. 三相三线制中的应用原理

在三相电路中，三相电压用U_sa、U_sb、U_sc，则三相电压可表示为：

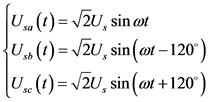(1)

其中U_s为电源电压的有效值。三相电流分别用i_a、i_b、i_c 表示，则可知：

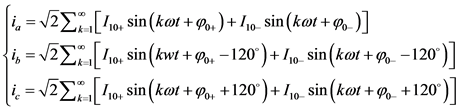(2)

其中I₁₀₊、I₁₀₋用来表示三相正序和负序电流值。当我们对电力系统的瞬时三相电流使用i_p、i_q法进行检测时，用a相电压相位角的值和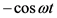来代替三相电压值 [6] 。在基本原理的具体内容中，为了更方便描述各种相关的变量，将旋转a-b-c坐标系中的电流电压值通过C₃₂变换转换到静止α-β垂直坐标系中，i_a、i_b、i_c则转换成i_α、i_β，U_sa、U_sb、U_sc转换成U_α、U_β。然后再通过C变换为电流i_p、i_q。有功电流和无功电流瞬时值i_p、i_q通过低通滤波器后，得到电流的直流分量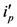、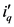，再经过坐标反变换方式(即C⁻¹·C₃₂)可以求得基波中正序有功电流的对应量i_a1、i_b1、i_c1。将测得负载电流值同基波分量相减，即为所求三相电流中谐波含量值i_ah、i_bh、i_ch 。其检测方法的运算原理图见图1。

图中：

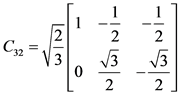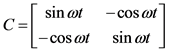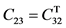, , (3)

2.2. 三相四线制系统中的推广研究

在380 V低压网系统中，三相四线制应用广泛，与三相三线制系统不同之处是，当电压不平衡或负载不平衡时，会导致中线中有零序电流产生，而这种现象是现在电力系统中普遍存在的。因为零序电流的影响，传统i_p-i_q法不能在三相四线制的低压网中直接应用。针对上述问题，首先进行理论的推广验证，验证在该系统下i_p-i_q法检测时不受零序电流存在的影响。

在式(2)中已经定义三相电流，则可知每相中所包含的零序电流相同，即：

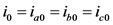(4)

应用前面提到的 C₃₂矩阵变换，并将式(2) (3)带入可得

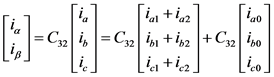(5)

式中

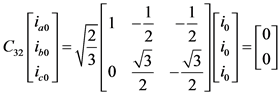(6)

Figure 1. The operating method of i_p-i_q

图1. i_p-i_q法运算原理图

则有：

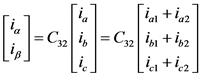(7)

再进行C变换得到i_p、i_q ，此时由于i_α、i_β 经变换后已不含有零序电流分量，所以再转换到与电力系统基波频率同步旋转的坐标系中时，i_p、i_q 也不会有零序电流分量 [7] 。经过LPF的滤波作用后得到其直流分量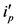、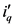，所得电流值进行坐标反变换后即为a-b-c坐标系中基波分量，此时用所得的基波分量再与负载处得到的电流值相减，即为指令值。因此,影响谐波电流检测效果的关键是LPF的设计。

3. 优化谐波算法分析

3.1. 系统的拓扑结构

在该系统中，常见的拓扑结构有两种，一种是电容的分裂式，第二种是四相桥臂式。第二种的结构里增加的一组桥臂为零线电流做补偿，令其产生与中线上原存在电流值相等而方向相差180度的，补偿电流以达到抵消中线电流的目标。但是同时使得控制更加复杂，成本增加，因此如图2所示本文应用的拓扑模型为三桥臂模型。

3.2. 低通滤波器的改进

在提取直流分量时，我们一般利用LPF来完成此项任务。在传统低通滤波器设计过程中，将截止频率的取值变小，谐波含量的检测精度会更高，但无法避免的，动态响应的速度就将变慢。相反，则会动态响应快，同时检测的精度会变低 [8] [9] 。在传统低通滤波器中动态响应速度和谐波检测精度无法同时保证的问题是很难解决的。因此，本文提出用电流平均值模块来解决传统结构中的弊病。

电流平均值法在传统的方法上进行了调整，主要的区别在于令i_p、i_q 的平均值模块来替代LPF部分。对三相电路的负载电流作傅里叶变换,再带入 C 变换可得到i_p、i_q值：

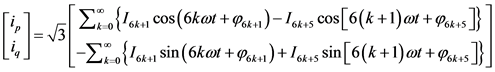(8)

Figure 2. Topology of APF

图2. APF拓扑结构

我们可以看出谐波中(6n + 1)次和(6n + 5)次会变成6n次和(6n + 6)次，均为6的倍数 [10] 。可以得知，将i_p、i_q在T/6内 积分运算后，获得的非零平均值即需要求得的基波分量中直流分量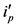、 ，再用式(6)中i_p、i_q值减去直流量，即为谐波电流。如图3所示为优化后谐波检测过程。

4. 仿真分析

在Simulink环境进行改进后的谐波检测算法的模拟仿真分析，根据图2中的APF拓扑结构图建立了相关模型。相关参数有：三相电源电压是380 V/50 Hz；三相整流桥中阻感负载R = 10 Ω，L = 4 mH；输入信号的采样频率12.8 kHz；直流侧电容值3300 µF。图4为负载电流波形，其THD = 29.26%。

图5为采用传统LPF检测算法A相的波形和三相谐波的电流波形。可以看出基于瞬时无功补偿理论的检测谐波的方法可以有效的得到负载电流里基波含量和谐波波形。

图6为改进后电流波形图。在与图5中测得的基波波形图对比中可以看出，采用传统方法和改进后的方法所测得的基波波形是相一致的。但是传统检测波形与改进后的检测波形对比，传统检测方法跟踪速度比较慢，至少需要一个周期才可跟踪到基波电流，而改进的方法仅仅在T/6的时间内就完成了准确跟踪系统基波电流的要求。改进后不仅提高了检测谐波的速度，在精度上也有很大提高。

如图7所示，是在瞬时无功理论i_p-i_q方法时波形畸变率，THD = 0.47%。通过对传统滤波器LPF的改进后，对其电流进行傅里叶分析，可得THD = 0.07%。由此可以看出，用电流平均值方法来改进传统低通滤波器LPF，对谐波检测来说是更加有效的。

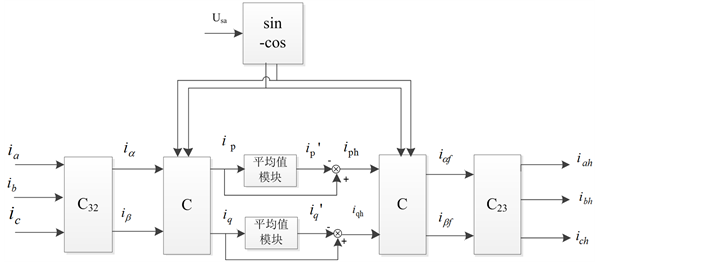
Figure 3. Sketch of improved harmonic detection method

图3. 优化谐波算法原理图

Figure 4. The load current wave and fundamental wave spectrum

图4. 系统负载电流及频谱分析

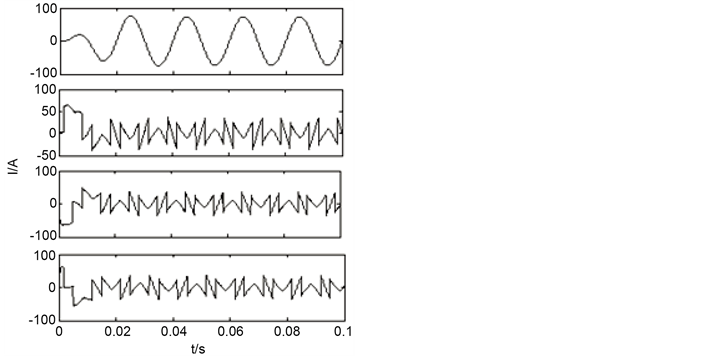
Figure 5. The fundamental and harmonic wave through the method of i_p-i_q

图5. i_p-i_q法测得基波与谐波波形

Figure 6. Phase A waveform of the improved method

图6. 改进后基波电流

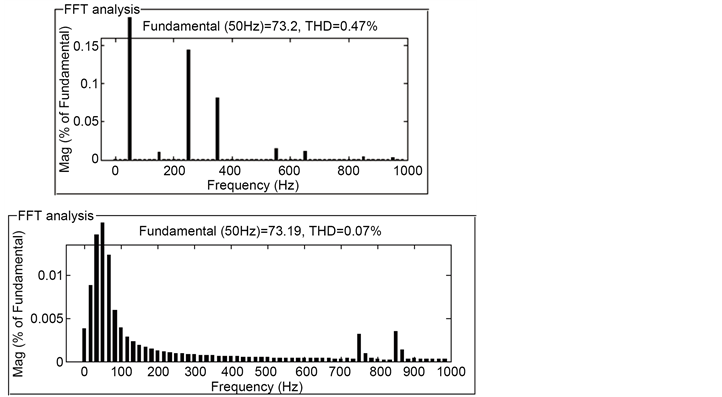
Figure 7. The spectrum of using the two methods

图7. 两种方法下的频谱图

5. 结束语

本文为了探究电力系统中如何有效解决中线内存在零序电流的问题，以瞬时无功理论为基础，使用电流平均值法替换了LPF模块，增强运行速率和检测精确性。然后通过Simulink仿真，验证改进后的检测方法的可行性，响应速度大大提高。为低电压配电网络中谐波电流装置的检测环节提供了新思路。

基金项目

中国博士后科学基金(2015T80729)；青岛市博士后研究人员应用研究项目资助(2015190)。