1. 引言
自然科学中的定律及原理是用偏微分方程来表达的,因而偏微分方程是联结数学与自然科学的关键性纽带,求解偏微分方程的显示解,特别是行波解,在理论和实际中有重要的作用,并受到数学和物理学家的广泛关注。许多数学工具和方法被用来求解非线性偏微分方程的行波解。如反散色法 [1] ,Backlund法 [2] ,Darboux变换法 [3] ,Hirota双线性法 [4] ,延拓法 [5] ,Painleve分析法 [6] ,有限差分法 [7] ,Tanh法 [8] 和Sin-Cos法 [9] ,首次积分法 [10] ,试探函数法 [11] 等。由于非线性偏微分方程形式和特征的多样性,尚无一种适用于求解所有类型偏微分方程的方法。
本文研究如下广义KDV方程的行波解
 (1)
(1)
其中,分数阶微分算子 是Jumarie的修正Riemann-Liouville导数 [12] ,其定义如下:
是Jumarie的修正Riemann-Liouville导数 [12] ,其定义如下:
 (2)
(2)
 为Gamma函数,定义为:
为Gamma函数,定义为:
 (3)
(3)
Jumarie的修正Riemann-Liouville导数有如下性质:
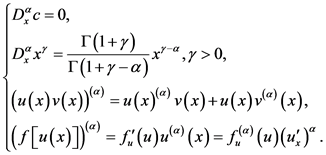 (4)
(4)
显然,方程(1)为一类典型的非线性偏微分方程。分数阶非线性偏微分方程是整数阶非线性偏微分方程的自然推广,可以解释许多整数阶非线性偏微分方程无法解释的现象,因而得到了生物、化学、物理、数学等领域学者的广泛关注和高度重视。现已广泛运用到流体力学 [13] 、生物医学 [14] 、固态物理 [15] 等工程领域,并对这些领域的发展产生了深远的影响。寻求分数阶微分方程的精确解已成了数学工作者的重要研究课题,得到了一些求解分数阶非线性方程的方法。如分数阶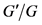 展开法 [16] ,分数阶子方程法 [17] ,分数阶微分变换法 [18] ,分数阶同伦扰动法 [19] 等。
展开法 [16] ,分数阶子方程法 [17] ,分数阶微分变换法 [18] ,分数阶同伦扰动法 [19] 等。
最近,Li Zheng Biao和He Ji Huan等人提出了分数阶复变换法 [20] ,运用该方法可将分数阶偏微分方程转化为整数阶偏微分方程。本文将分数阶复变换法与Cn函数展开法 [21] 相结合,求解了分数阶广义的KDV方程(1)。最终,我们获得了方程(1)的周期解和孤立波解,当分数阶导数 时,所得到的精确解就是通常的行波解,大大丰富了此方程的解系,为专家学者在某些问题的研究上提供了帮助。
时,所得到的精确解就是通常的行波解,大大丰富了此方程的解系,为专家学者在某些问题的研究上提供了帮助。
2. 复变换-Cn函数展开法
基于复变换方法和Cn函数展开法,得到下面的复变换-Cn函数展开法,该方法主要步骤如下:
第一步,考虑如下分数阶微分方程:
 (5)
(5)
其中 是代数函数
是代数函数 关于自变量t和x的Jumarie的修正Riemann-Liouville导数,P是关于函数u及偏导数的多项式,P中含有最高阶导数和非线性项。
关于自变量t和x的Jumarie的修正Riemann-Liouville导数,P是关于函数u及偏导数的多项式,P中含有最高阶导数和非线性项。
作分数阶复变换:
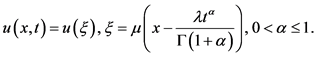 (6)
(6)
其中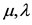 是常数,当
是常数,当 时,式(6)就是通常的行波变换,在式(6)的作用下,式(5)变为:
时,式(6)就是通常的行波变换,在式(6)的作用下,式(5)变为:
 (7)
(7)
第二步,假设(7)式的解u可以表示为C的多项式形式:
 (8)
(8)
其中 是待定常数,
是待定常数, 。正整数K通过式(7)中的最高阶导数项和非线性项来确定。
。正整数K通过式(7)中的最高阶导数项和非线性项来确定。
记 ,由椭圆函数的导数公式有:
,由椭圆函数的导数公式有:
 (9)
(9)
若以 表示u的最高幂次的次数K,则
表示u的最高幂次的次数K,则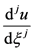 最高幂次的次数应为:
最高幂次的次数应为:
 (10)
(10)
而 的最高幂次的系数为
的最高幂次的系数为
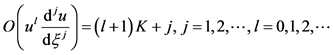 (11)
(11)
将(8)式代入(7)式,平衡方程(7)中的最高阶导数项和非线性项的幂次,可以确定参数K的值,同时利用(9)式等可以导出代数方程
 (12)
(12)
其中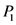 和
和 为C的多项式,令
为C的多项式,令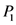 和
和 中C的各幂次系数为零,便得到确定
中C的各幂次系数为零,便得到确定 及
及 和
和 的代数方程组。运用Wu消元法求解这个代数方程组,就得到(5)式的形如(8)的周期波解。特别地,令模数
的代数方程组。运用Wu消元法求解这个代数方程组,就得到(5)式的形如(8)的周期波解。特别地,令模数 ,就可以得到相应的孤立波解。
,就可以得到相应的孤立波解。
3. 分数阶广义KDV方程
考虑如下分数阶广义KDV方程:
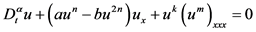 (13)
(13)
对(13)式作复变换:
 (14)
(14)
经过整理变形,方程(14)化为
 (15)
(15)
假设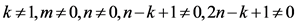 。对方程(15)积分,并忽略积分常数,得到关于
。对方程(15)积分,并忽略积分常数,得到关于 的二阶常微分方程
的二阶常微分方程
 (16)
(16)
平衡式(16)中的最高阶导数项和非线性项得到
 (17)
(17)
所以
 (18)
(18)
情况3.1 当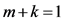 时,方程(16)化为
时,方程(16)化为
 (19)
(19)
令 ,代入到(19)中得到
,代入到(19)中得到
 (20)
(20)
假设式(20)具有如下形式解
 (21)
(21)
平衡式(20)中最高阶导数项和非线性项得到K = 1,将(21)代入式(20),其中
 (22)
(22)
合并C相同幂次,并令每一项系数为零,得到一组关于 的方程组
的方程组
 (23)
(23)
借助Wu消元法求解方程组得到
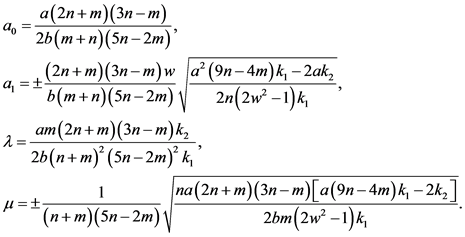 (24)
(24)
其中
 (25)
(25)
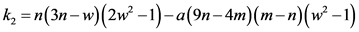 (26)
(26)
于是
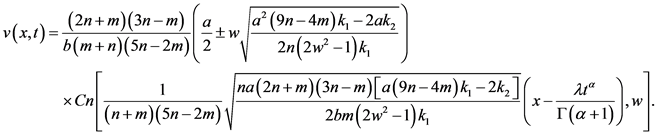 (27)
(27)
特别的,当 时
时
 (28)
(28)
其中 ,
, 的值由上给出,因此得到广义KDV方程精确解如下:
的值由上给出,因此得到广义KDV方程精确解如下:
 (29)
(29)
 (30)
(30)
情况3.2当 时,方程(16)化为
时,方程(16)化为
 (31)
(31)
令 ,代入到(31)得到
,代入到(31)得到
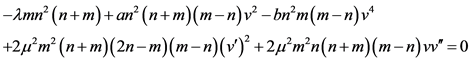 (32)
(32)
假设式(31)具有如下形式解
 (33)
(33)
平衡式(32)中最高阶导数项和非线性项得到K=1,将(33)代入式(32),合并C的相同幂次,并令每一项系数为零,得到一组关于 的方程组
的方程组
 (34)
(34)
借助Wu消元法求解方程组得到
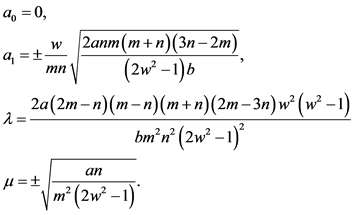 (35)
(35)
于是
 (36)
(36)
特别的,当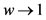 时
时
 (37)
(37)
其中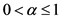 ,
, 的值由上给出.因此得到广义KDV方程精确解如下:
的值由上给出.因此得到广义KDV方程精确解如下:
 (38)
(38)
 (39)
(39)
4. 结语
将分数阶复变换方法和Cn函数展开法相结合,得到了求解分数阶非线性方程的精确解的一种新方法。本文求解了广义KDV方程,得到了此方程的新的精确解。当分数阶导数 时,所得到的精确解就是通常的行波解。
时,所得到的精确解就是通常的行波解。
基金项目
四川省杰出青年基金(2014JQ0039),国家自然科学基金(11501395)。