1. 引言
算法分析与设计课程是计算机科学与技术专业的专业课,在王晓东老师出版的《计算机算法设计与分析》 [1] 中主要介绍了计算机科学技术领域中的六大类经典的算法设计思想,包括:分治法、动态规划法、贪心算法、回溯法、分枝限界法、随机化算法,其中的贪心算法是非常常用的一类算法。教材中通过一些实例来加深学生对贪心算法思想的理解和运用,比如最优装载问题、背包问题、活动安排问题、哈夫曼编码、多机调度问题等。然而在实践教学中发现,对于贪心算法的思想,学生们掌握起来比较容易,但是如果要判断是否能够通过贪心算法求得问题的最优解,则存在较大的困难。如果想要通过贪心算法来求得问题的最优解,必须证明所选择的贪心选择策略满足两个性质:贪心选择性质和最优子结构性质。因此,如何进行证明是关键。
为此,本文以贪心算法求解最优装载问题为例,提出一种将动画、实例和证明中使用的形式化描述相结合的教学方法。经实践检验,这种方法的教学效果较好。相比于已有的一些相关研究 [2] [3] [4] ,本文提出的方法具有较强的可操作性。
2. 用贪心算法求解最优装载问题
以人类的理解能力而言,对图的理解要好于对文字的理解。在介绍抽象内容时,如果能够辅以图或动画,往往能够达到事半功倍的效果。算法设计类教材中,对于每类算法设计思想,通常都会选择若干实际的例子,通过对例子的讲解来加深学生的理解和认识。但是即便如此,对于一些较抽象的内容,学生理解起来依然十分费力。下面以贪心算法中的一个教学难点为例,介绍如何通过实际例子,辅以动画的效果,来更为形象的展示抽象理论知识的讲解,从而帮助学生更好的理解。
贪心算法的基本思想是:在选择时,每次都做出在当前看来是最好的选择。也就是在做选择时并不考虑全局最优,而是每次仅考虑局部最优。这就带来两个问题:1) 如果每次都只做局部最优的选择,是否最后一定能够达到全局最优?2) 满足何种条件才能保证局部最优的选择会带来全局最优的结果?
第1个问题,答案是否定的,对于学生来说也比较好理解。在使用贪心算法求解时,需要制定贪心策略,也就是你到底是依据什么来进行选择。不同的人所制定的贪心策略有可能并不相同,也就是对同一个问题可以存在多种选择策略,而并非每种选择策略都会得到全局最优的结果。
第2个问题是教学的难点。既然局部最优未必能够得到全局最优,那如果我们的目的就是要得到全局最优怎么办?贪心算法还能不能用?这时,可引出两个性质:贪心选择性质和最优子结构性质。如果我们能够证明,依据所选定的贪心策略,可以满足贪心选择性质和最优子结构性质,那么,我们就可以通过一次次的局部最优的选择得到全局最优的结果。而如何证明这两个性质,是教学的难点。
为了解决这个问题,通过一个具体的例子,设计了相应的动画,和形式化的证明过程相结合,来降低学生在理解上的难度。
下面以最优装载问题为例来进行说明。最优装载问题:有一批集装箱要装上一艘载重量为c的轮船。问题:在装载体积不受限制的情况下,如何能将尽可能多的集装箱装上轮船?
在讲解过程中,首先引导学生对问题进行形式化的描述:
c——轮船载重量
n——集装箱的个数
xi——第i个集装箱是否被选中,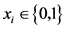
wi——第i个集装箱的重量
为了让学生有更直观的认识,将该问题通过具体的数值实例化。
有5个集装箱,轮船的载重量为19。
各集装箱的重量如表1所示。
由于有具体的实例,所以学生们可以很容易的来寻找可能的解。如果用1表示该集装箱被选中,用0表示未被选中,则可能的解有:
(1,1,1,0,0)
(1,1,0,1,0)
(0,0,1,1,0)
……
由于每个箱子都有选中和未选中2个状态,所以5个箱子的解空间为25。
从例子可知若用穷举法进行解空间的搜索,代价是非常大的。那么此例是否可用贪心算法来求解?贪心策略如何制定?用贪心算法能否求得最优解都是我们关心的问题。
由于目标是装载最多的集装箱,所以很容易想到,可以制定如下的装载策略:最轻的先装。依据这个策略,进行集装箱的选择,是否能够得到整体最优解,即:装载最多的集装箱?需要证明在此策略下,满足最优子结构性质和贪心选择性质。
在介绍贪心算法时,可以跟学生强调,贪心算法常用于求解最优化问题,但是用贪心算法并不总能得到最优解。
在进行两个性质的证明前,还需要学生从总体上了解贪心算法的解题步骤。贪心算法求解问题的基本步骤如下:
(1) 做出在当前看来最好的选择(贪心选择)。
(2) 每选择一次,完成原问题的一部分,使问题规模缩小。
(3) 继续进行贪心选择,如此反复,直至得到最终解。
上述基本步骤,通过例子可以很好的让学生理解。
依据分析可知我们的选择策略为“最轻的先装”。按照这个策略,可以首先将集装箱按照重量进行排序,然后在满足条件的情况下依次进行选择。排序后的集装箱如表2所示。
假如用一个大的圆来表示集装箱的剩余载重量,具体数值由圆心的数字表示。那么每做一次选择,圆的大小及圆心的数字都会变小,从而直观的体现求解的过程。

Table 1. Candidate containers table
表1. 可选集装箱情况表

Table 2. Sorted candidate containers table
表2. 排序后的可选集装箱情况表
比如,初始时可用下图表示:

按照最轻的先装的策略,第1次选择重量为3的集装箱。做完这次选择后,轮船的剩余载重量变化为:
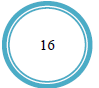
继续进行选择,第2次选择重量为5的集装箱。做完这次选择后,轮船的剩余载重量变化为:

继续进行选择,第3次选择重量为6的集装箱。做完这次选择后,轮船的剩余载重量变化为:

而此时,剩余的集装箱均无法装上轮船。每一次选择,我们都选择当前可选范围内重量最轻的集装箱,直至无集装箱可以被选择为止。由此,我们得到了问题的解。
由于此例非常简单,即使不用证明,学生也知道所得的解确实是该问题的最优解。但是对于一些比较复杂的情况,是无法简单进行判断的。因此,还是需要依赖于证明。下面就两个性质的证明进行介绍。
1) 贪心选择性质的证明:贪心选择性质是指所求问题的整体最优解可以通过一系列局部最优的选择(贪心选择)来达到。贪心选择性是贪心算法可行的第一个基本要素。
通过所选案例,如果进行简单的思考,可以发现,其实贪心算法问题的最优解,可能不止一个。比如,在此例中,如果选择的集装箱分别为重量是5,6,8的集装箱,依然满足要求。所以,在进行贪心选择性质的证明时,我们可以倒推。即,假设我们通过贪心选择策略得到的解就是已知问题的最优解,但这个解不满足我们的贪心选择策略(即:每次都选择最轻的集装箱)。那么,如果我们可以把这个解进行改造,使得改造后的解满足我们的贪心选择策略,则可知,若一开始就按照贪心选择策略进行选择,得到的依然是问题的最优解。
那如何进行改造即是我们证明的关键。
用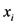 表示集装箱的选中状态,设
表示集装箱的选中状态,设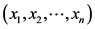 为最优解,
为最优解,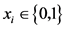 。
。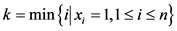 为被选中的最轻的集装箱的编号。
为被选中的最轻的集装箱的编号。
对应到此例中,选中的为重量为5,6,8的集装箱,则最优解为(0,1,1,1,0)。其中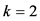 。
。
如果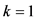 ,说明当前的解是以贪心选择开始的最优解,也就是说当前解的第一次选择和采用贪心选择策略进行的选择是一样的。
,说明当前的解是以贪心选择开始的最优解,也就是说当前解的第一次选择和采用贪心选择策略进行的选择是一样的。
如果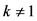 ,则将当前的第1个集装箱和第k个集装箱的选中状态进行交换。则在此例中,解变换为(1,0,1,1,0)。
,则将当前的第1个集装箱和第k个集装箱的选中状态进行交换。则在此例中,解变换为(1,0,1,1,0)。
对应的形式化描述为:
若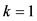 ,
,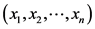 为以贪心选择开始的最优解。
为以贪心选择开始的最优解。
若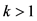 ,取
,取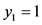 ,
, ,
,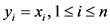 ,
, ,则:
,则: 。由
。由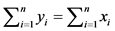 可知,
可知,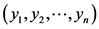 是以贪心选择开始的最优解。
是以贪心选择开始的最优解。
进行完第一次选择之后,继续重复此过程,直到每一次选择都符合贪心策略,从而得到一个整体满足贪心选择策略的解。由整个过程可知,该解也是问题的最优解。
整个过程可将动画和具体例子与形式化证明相结合,比如先通过动画展示选择和交换的过程,然后再显示形式化的证明。这样一方面让学生了解具体的问题是如何形式化为数学模型进行描述和证明的,另一方面简化学生的理解难度并加深印象。
2) 最优子结构性质的证明:问题的最优解包含其子问题的最优解时,称此问题具有最优子结构性质。问题的最优子结构性质是该问题可用贪心算法求解的关键特征。
最优子结构性质通常通过反证法进行证明。
对应到此例中,按照贪心策略得到的最优解为选中重量为3,5,6的集装箱,即最优解为(1,1,1,0,0)。
可知,对于可选集装箱重量为5,6,8,9,轮船载重量为16的最优装载问题而言,(1,1,0,0)为其最优解。其形式化的证明如下:
若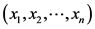 是轮船载重量为 时的最优解,易知
是轮船载重量为 时的最优解,易知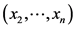 是轮船载重量为
是轮船载重量为 时相应子问题的最优解。若不然,设
时相应子问题的最优解。若不然,设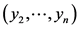 是相应子问题的最优解,则:
是相应子问题的最优解,则: ,与假设矛盾。
,与假设矛盾。
将形式化的描述符号和例子中的具体数据相结合,使得各项数据更加的易于理解。在动画中用不同的颜色代表集装箱的不同状态,如可用红色表示选中状态,绿色代表未选中状态。
经过几轮授课,分别采用只有形式化证明,没有具体例子;有具体例子和形式化证明;有具体例子,形式化证明和辅助动画三种形式,发现第三种形式学生的理解和接受效果最好。通过这个例子,学生更深入的理解了贪心算法的精髓和使用贪心算法求解最优化问题的关键。
3. 结束语
众所周知,动画的运用使我们的授课更加的生动,在实践中发现,对于如贪心算法类似的抽象内容的讲解,如果能将动画与抽象的理论和具体的实例相结合,对提高学生的学习积极性,增强对抽象知识点的理解能力有极大的帮助。
基金项目
北京信息科技大学2016年教学改革项目;北京市教委专项:教师队伍建设–教师教学促进–外培计划教师教学能力提升项目(市级)–计算机科学与技术;教师队伍建设–教师教学促进–双培计划虚拟教学团队建设(市级)–计算机科学与技术、软件工程。