马尔可夫调制的Kaldor-Kalecki模型的随机稳定性仿真研究

Simulation of Stochastic Stability of Kaldor-Kalecki Model with Markovian Switching

摘要: 本文研究了经济周期模型受到随机性波动及两状态马尔可夫链切换的影响，通过利用随机稳定性方法探讨了在给定参数条件下的具有时滞的Kaldor-Kalecki模型的稳定性行为，得到了解的稳定性的仿真结果。

Abstract: This paper studies that the economic system is in the random environment which has Markov chain with two discrete values. By using the method of stochastic stability and the given parameters, the stability of the solution of the random Kaldor-Kalecki model with Markovian Switching is discussed, and the illustrative simulation is obtained.

1. 引言

现实的经济系统由于受到不确定性的因素影响，因此可以用随机微分方程来简单描述一些经济系统。同时，这些社会经济的起伏变化，或者制定新的政策，或者新产品的市场进入会带来经济系统结构性的改变，因此经济系统中引入具有离散状态特征的马氏链比较合适。

近十年来，具有马尔可夫链的随机微分方程与随机时滞微分方程大量应用于经济管理，金融工程，生物动态模型，疾病预防控制及神经网络等领域，其相应的理论与软件仿真也得到了较大的发展，尤其在随机稳定性及几乎必然指数稳定性研究等方面。

而在具体的经济周期模型应用方面，具有马氏链的随机时滞微分方程的研究较少，本文考虑到经济系统也总是处于经济周期性波动的扩张与紧缩两种状态，因此引入两状态的马尔可夫链到动态的Kaldor-Kalecki模型中，研究它的相应稳定性及其数值仿真结果。

2. 预备知识及模型构建

Mao (2001)研究了如下的马尔可夫调制的随机微分方程 [1] :

$\text{d}x\left(t\right)=f\left(x\left(t\right),x\left(t-\tau \right),t,r\left(t\right)\right)\text{d}t+g\left(x\left(t\right),x\left(t-\tau \right),t,r\left(t\right)\right)\text{d}w(t)$

这里 $t\ge 0$ ，具有初始值 $x_0\in C_{F_0}^b\left(\Omega ;R^n\right),f:R^n\times R_{+}\times S\to R^n,g:R^n\times R_{+}\times S\to R^{n\times m}$ 。

设 $|\cdot |$ 表示Rⁿ中欧氏范数，假如A是一个矩阵(用A^T表示A的转置)，则定义其迹范数为 $|A|=\sqrt{trace\left(A^{\text{T}}A\right)}$ ，定义算子范数为 $\Vert A\Vert =\sup \left\{|Ax|:|x|=1\right\}$ 。设 $r\left(t\right),t\ge 0$ 是定义在完备概率空间

$\left(\Omega ,F,{\left\{F_t\right\}}_{t\ge 0},P\right)$ 上的右连续马尔可夫链，取两个值的状态空间 $S=\left\{1,2,\cdots ,N\right\}$ ，且具有生成元 $\Gamma ={\left({\gamma }_{ij}\right)}_{N\times N}$ ，其中

$P\left\{r\left(t+\Delta \right)=j|r\left(t\right)=i\right\}=\{\begin{array}{l}{\gamma }_{ij}\Delta +o\left(\Delta \right),i\ne j\\ 1+{\gamma }_{ij}\Delta +o\left(\Delta \right),i=j\end{array}$

这里 $\Delta >0$ ， ${\gamma }_{ij}\ge 0$ 是由i状态转移到j状态的转移速率，且 ${\gamma }_{ii}=-{\displaystyle \underset{j}{\sum }{\gamma }_{ij}},i\ne j$ 。

假设马尔可夫链 $r\left(t\right)$ 与布朗运动 $w(•)$ 相互独立，则 $r\left(t\right)$ 的每一个样本轨道几乎都是一个右连续的阶梯函数。

对 $V\in C^{2,1}\left(R^n\times R_{+}\times S;R_{+}\right)$ ，定义算子 $LV$ 如下

$\begin{array}{c}LV\left(x,t,i\right)=V_t\left(x,t,i\right)+V_x\left(x,t,i\right)f\left(x,y,t,i\right)\\ +\frac{1}{2}trace\left[g^{\text{T}}\left(x,y,t,i\right)V_{xx}\left(x,t,i\right)g\left(x,y,t,i\right)\right]+{\displaystyle \underset{j=1}{\overset{N}{\sum }}{\gamma }_{ij}V\left(x,t,j\right)},\end{array}$

这里 $V_t\left(x,t,i\right)=\frac{\partial V}{\partial t},V_x\left(x,t,i\right)=\left(\frac{\partial V}{\partial x_1},\cdot \cdot \cdot ,\frac{\partial V}{\partial x_n}\right),V_{xx}\left(x,t,i\right)={\left(\frac{{\partial }^{2}V}{\partial x_i{x}_j}\right)}_{n\times n}$ 。

Kaldor (1940)分析了Kaldor模型 [2] ，

$\{\begin{array}{l}\stackrel{\dot{}}{Y}\left(t\right)=\alpha \left(I\left(Y,K\right)-S\left(Y,K\right)\right),\\ \stackrel{\dot{}}{K}\left(t\right)=I-\delta K.\end{array}$ (1)

Kalecki (1935)通过将投资依赖于投资决定做出的时机的收入和投资完成的时机的资本存量，考虑到了资本积累方程 [3]

$\stackrel{\dot{}}{K}\left(t\right)=I\left(Y\left(t-\tau \right),K\right)-\delta K$

这里 $\tau \ge 0$ 指常数时间延滞， $\delta \ge 0$ 指资本存量的折旧率。

M. Szydlowski and Krawiee A. (2001, 2001)分析了Kaldor-Kalecki模型 [4] [5] ，

$\{\begin{array}{l}\stackrel{\dot{}}{Y}\left(t\right)=\alpha \left(I\left(Y,K\right)-S\left(Y,K\right)\right),\\ \stackrel{\dot{}}{K}\left(t\right)=I\left(Y\left(t-\tau \right),K\right)-\delta K.\end{array}$ (2)

令 $I\left(Y,K\right)=\gamma I\left(Y\right)-\gamma K$ ， $I\left(Y\right)=\upsilon Y$ ， $\gamma >0$ ， $I\left(Y\left(t-\tau \right),K\right)=\gamma I\left(Y\left(t-\tau \right)\right)-\gamma K=\gamma \upsilon Y\left(t-\tau \right)-\gamma K$ ，

$\{\begin{array}{l}\stackrel{\dot{}}{Y}\left(t\right)=\alpha \left(\gamma \upsilon -s\right)Y\left(t\right)-\alpha \gamma K\left(t\right),\\ \stackrel{\dot{}}{K}\left(t\right)=\gamma \upsilon Y\left(t-\tau \right)-\left(\gamma +\delta \right)K\left(t\right).\end{array}$ (3)

将方程(3)写成矩阵形式

$\text{d}X\left(t\right)=\left(AX\left(t\right)+BX\left(t-\tau \right)\right)\text{d}t$

这里 $X\left(t\right)=\left(\begin{array}{l}Y\left(t\right)\\ K\left(t\right)\end{array}\right)$ ， $A=\left(\begin{array}{cc}\alpha \left(\gamma \upsilon -s\right)& -\alpha \gamma \\ 0& -\left(\gamma +\delta \right)\end{array}\right)$ ， $B=\left(\begin{array}{cc}0& 0\\ \gamma \nu & 0\end{array}\right)$ 。

命题1：在满足条件 $\frac{\upsilon }{s}=\frac{1}{\gamma }+\frac{1}{\delta }$ 之下，则系统(3)存在唯一的均衡点 $\left(Y^{*},K^{*}\right)=\left(0,0\right)$ 。

命题2：由条件 $\frac{\upsilon }{s}=\frac{1}{\gamma }+\frac{1}{\delta }$ ，可得 $\gamma \upsilon >s$ ，同时 $\left|\begin{array}{cc}\alpha \left(\gamma \upsilon -s\right)& -\alpha \gamma \\ 0& -\left(\gamma +\delta \right)\end{array}\right|<0$ 。

由于此系统受到随机扰动的影响，令变量 $Y\left(t\right)$ ， $K\left(t\right)$ 和 $Y\left(t-\tau \right)$ 对应的参数在式(3)两个方程中分别受到强度为 ${\sigma }_{1}w\left(t\right)$ ， ${\sigma }_{2}w\left(t\right)$ ， ${\sigma }_{3}w\left(t\right)$ 和 ${\sigma }_{4}w\left(t\right)$ 的随机扰动( $w\left(t\right)$ 为定义在完备概率空间 $\left(\Omega ,F,{\left\{F_t\right\}}_{t\ge 0},P\right)$ 上的一维布朗运动)。

即模型(3)变为

$\{\begin{array}{l}\stackrel{\dot{}}{Y}\left(t\right)=\left(\alpha \left(\gamma \upsilon -s\right)+{\sigma }_{1}w\left(t\right)\right)Y\left(t\right)+\left(-\alpha \gamma +{\sigma }_{2}w\left(t\right)\right)K\left(t\right),\\ \stackrel{\dot{}}{K}\left(t\right)=\left(\gamma \nu +{\sigma }_{3}w\left(t\right)\right)Y\left(t-\tau \right)+\left(-\left(\gamma +\delta \right)+{\sigma }_{4}w\left(t\right)\right)K\left(t\right).\end{array}$ (4)

$\Rightarrow \{\begin{array}{l}\text{d}Y\left(t\right)=\left(\alpha \left(\gamma \upsilon -s\right)Y\left(t\right)+\left(-\gamma \right)K\left(t\right)\right)\text{d}t+\left({\sigma }_{1}Y\left(t\right)+{\sigma }_{2}K\left(t\right)\right)\text{d}w\left(t\right),\\ \text{d}K\left(t\right)=\left(\left(\gamma \upsilon \right)Y\left(t-\tau \right)-\left(\gamma +\delta \right)K\left(t\right)\right)\text{d}t+\left({\sigma }_{3}Y\left(t-\tau \right)+{\sigma }_{4}K\left(t\right)\right)\text{d}w\left(t\right).\end{array}$ (5)

用矩阵表示为

$\text{d}X\left(t\right)=\left(AX\left(t\right)+BX\left(t-\tau \right)\right)\text{d}t+\left(CX\left(t\right)+DX\left(t-\tau \right)\right)\text{d}w\left(t\right)$ (6)

其中 $C=\left(\begin{array}{cc}{\sigma }_1& {\sigma }_2\\ 0& {\sigma }_4\end{array}\right),D=\left(\begin{array}{cc}0& 0\\ {\sigma }_3& 0\end{array}\right)$ 。

同时假设模型(6)受到转换概率为P的两状态马尔可夫链切换，即

$\text{d}X\left(t\right)=\left(A\left(r\left(t\right)\right)X\left(t\right)+B\left(r\left(t\right)\right)X\left(t-\tau \right)\right)\text{d}t+\left(C\left(r\left(t\right)\right)X\left(t\right)+D\left(r\left(t\right)\right)X\left(t-\tau \right)\right)\text{d}w\left(t\right),$ (7)

这里 $r\left(t\right)=1,2$ 。生成元 $\Gamma =\left(\begin{array}{cc}{\gamma }_{11}& {\gamma }_{12}\\ {\gamma }_{21}& {\gamma }_{22}\end{array}\right),{\gamma }_{11}=-{\gamma }_{12}<0,{\gamma }_{22}=-{\gamma }_{21}<0$ 。

3. 案例仿真

例1，令

$\begin{array}{l}{\alpha }_1=0.011,{\gamma }_1=0.018,{\delta }_1=0.049,s_1=0.024,{\upsilon }_1=s_1\ast \left(1/{\gamma }_1+1/{\delta }_1\right);\\ {\alpha }_2=0.012,{\gamma }_2=0.017,{\delta }_2=0.056,s_2=0.031,{\upsilon }_2=s_2\ast \left(1/{\gamma }_2+1/{\delta }_2\right);\end{array}$

$C_1=\left(\begin{array}{cc}0.556& 0.635\\ 0& 0.621\end{array}\right),C_2=\left(\begin{array}{cc}0.548& 0.624\\ 0& 0.671\end{array}\right),D_1=\left(\begin{array}{cc}0& 0\\ 0.246& 0\end{array}\right),D_2=\left(\begin{array}{cc}0& 0\\ 0.225& 0\end{array}\right)$

$\Gamma =\left(\begin{array}{cc}-3& 3\\ 1& -1\end{array}\right),\tau =0.2$

通过使用Euler-Maruyama方法进行Matlab仿真，在不同随机样本下，得到图1~4。

由图1~4看出，随机Kaldor-Kalecki模型(7)的解在时间t < 20以内具有较为强烈的波动，而在t > 20以后，模型的解较为稳定且趋均衡解(平凡解)。因此，具有案例数值的随机Kaldor-Kalecki模型(7)在具有时滞及马尔可夫链切换的状态下具有稳定性。

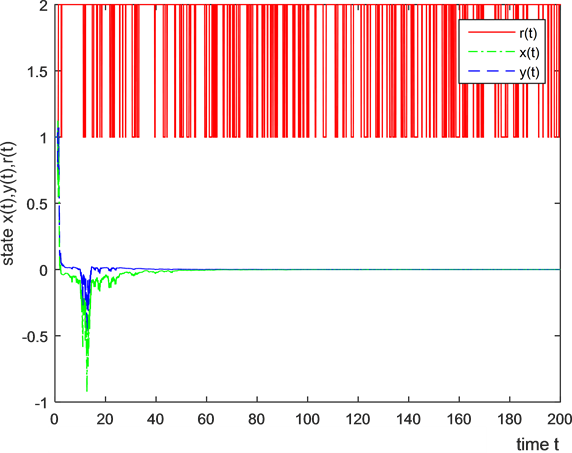
Figure 1. Solution x(t), y(t) of sde and r(t) under the first sample

图1. 第一个样本的随机微分方程解x(t), y(t)和马氏链r(t)

Figure 2. Solution x(t), y(t) of sde and r(t) under the second sample

图2. 第二个样本的随机微分方程解x(t), y(t)和马氏链r(t)

Figure 3. Solution x(t), y(t) of sde and r(t) under the third sample

图3. 第三个样本的随机微分方程解x(t), y(t)和马氏链r(t)

Figure 4. Solution x(t), y(t) of sde and r(t) under the fourth sample

图4. 第四个样本的随机微分方程解x(t), y(t)和马氏链r(t)

基金项目

教育部人文社会科学研究一般项目资助(11YJCZH259)。