使用差分方法提高预测精度——基于中国沪深300股票指数的实证分析

Using Difference Method to Improve the Prediction Accuracy—An Empirical Study Based on China Shanghai and Shenzhen 300 Stock Index

摘要: 当AR、ARIMA、ARMA、MA模型被用来进行时间序列未来值的预测时，由于误差项很容易被忽略掉，所以预测精度受到很大的影响。为了提高预测的精度，本文提出使用差分方法(DF)来处理自相关模型(AR)的误差项。通过对中国沪深300指数(Hushen300)进行实证研究发现：第一，AR-DF模型比单纯AR模型大大提高了HUSHEN收益指数实际值与预测值之间的相关系数；第二，AR-DF模型所得到的误差值比单纯AR模型要小很多；第三，在滞后阶数达到700时，AR-DF模型对于股票收益指数涨跌趋势的命中率比单纯AR模型提高了25.30个百分点，从50.99%提高到了62.65%。

Abstract: When prediction models such as AR, ARIMA, ARMA, and MA are usually used to forecast the future values of a time series, because the residual values are easily ignored, the prediction accuracy has been influenced a lot. For improving the prediction accuracy, this paper suggests use difference method (DF) to deal with the residual item of autoregressive model (AR). Based on the China Shanghai and Shenzhen 300 Stock Index (Hushen300), the empirical study has found: First, the AR-DF model can result in higher correlation between the real value of HUSHEN return index and its prediction value than pure AR model; second, the average residual value of AR-DF model is quite smaller than the pure AR model; Third, the hit ratio of AR-DF model has increased more than 25.30 percent points than pure AR model, which can increase from 50.99% to 62.65% when the lag order is up to 700.

1. 文献综述

一般来说，在金融市场上，对股票收益指数(或收益率) $r_t$ 预测的目的，就是希望寻找出一个合适的预测模型 $r_t=f\left(\cdot |F_{t-1}\right)$ 。信息集 $F_{t-1}$ 被假设为包含在时间区间 $t\in \left[0,t-1\right]$ 范围内的所有已知信息，特别是当时间变量从 $t=0$ 向 $t=t-1$ 变化时，信息集包含了所有与股票价格和收益指数相关的历史信息。一个好的预测模型，就是能够在信息集 $F_{t-1}$ 基础上，对时间变量 $t$ 时的股票价格和收益指数做出符合实际预测的回归模型。很显然，为了得到一个好的预测模型，以往的历史数据值往往起着关键的作用，是建立模型的基础。

在完全有效市场中，股票价格和收益指数的精确走势是不可预测的。完全有效市场假设在金融市场研究中金融变量服从随机游走规律，即投资者对于未来资产价格的投机性预测是不可能的，因为，如果收益指数是可以预测的，那么，许多投资者都会去预测资产的未来收益价格，从而追逐并得到无穷利润，这在现实中是不可能的。现实经济环境往往与完全有效市场假设差异很大(Timmermann & Granger, 2004) [1] ，也就是说，现实市场往往是非完全有效市场，投资者对于未来资产价格的预测是有意义的。

在预测模型的研究过程中，一个很重要的任务就是分析时间序列变量，构建合适的预测模型。

许多研究者都喜欢使用AR自相关模型或者VAR向量自相关模型来实现在金融市场上对金融变量进行预测的目的(Chen & Lin, 2011) [2] 。AR自相关模型主要用来处理具有自相关性的单变量时间序列的建模问题，而VAR向量自相关模型主要用来处理具有自相关性的多变量时间序列的建模问题。

当资产收益指数的初始随机时间序列具有非稳定状态的时候，ARIMA自相关协整移动平均模型比较适合作为预测模型(Shih & Tsokos, 2008) [3] 。ARIMA模型自诞生以来(Box & Jenkins, 1970) [4] ，在非平稳时间序列预测模型建立方面已经得到了极大的应用。相反地，当资产收益指数的初始随机时间序列具有稳定状态的时候，由于时间序列水平变量是平稳变量，没有单位根，所以，ARMA自相关移动平均模型比较适合作为预测模型。

因为任何非平稳时间序列都可以通过高阶差分运算化简为平稳序列，所以，对于一般平稳时间序列而言，人们经常使用的预测模型除了ARMA模型之外，还有简单的AR自相关模型和MA移动平均模型。AR自相关模型是最为简单的一种模型，因此，它的应用极为普遍。

AR、MA、ARMA、ARIMA等模型，都是与时间序列自回归相关的预测模型，对于模型误差项的处理，将直接影响着模型的预测精度。

假如回归模型的误差项为 $a_t$ ，一般都假设误差项 $a_t$ 具有均值 $E\left(a_t\right)=0$ ，方差 $VaR\left(a_t\right)={\sigma }_a^2$ 。当使用这些模型进行预测时，一般都简单地假设 $a_t=E\left(a_t\right)=0$ ，例如Shih & Tsokos (2008) [3] 的研究。

因为回归模型的误差项通常包含了几乎所有来自私人的信息、来自宏观经济的冲击信息、以及来自某些未知源的信息，所以，误差项对于回归预测的影响很大，这也正是MA移动平均模型专门考虑误差项的原因。但是，当回归模型的误差项 $a_t$ 以 $a_t=0$ 的形式被简单地忽略掉时，例如Shih & Tsokos (2008) [3] 的研究，预测模型的精确性将受到很大的影响。

虽然在假设误差项 $a_t=0$ 时，人们无法得到精确的预测值；但是，通过引入动态方差，人们却可以定出预测值的边界。ARCH自回归条件异方差(Engle, 1982) [5] 和GARCH一般自回归条件异方差(Bollerslev, 1986) [6] 模型通常被用来计算动态方差值。当AR自回归过程 $r_t={\mu }_t+a_t$ 模型被用来开展预测时，基于历史

信息集 $F_{t-1}$ ，随机变量 $r_t$ 的条件期望值可以表示为 $E\left(r_t|F_{t-1}\right)={\mu }_t={\alpha }_0+{\alpha }_1{r}_{t-1}+\cdots +{\alpha }_p{r}_{t-p}$ ，其动态条件方差可以表示为 $Var\left(r_t|F_{t-1}\right)={\sigma }_t^2$ ，即 $r_t|F_{t-1}~N\left({\mu }_t,{\sigma }_t^2\right)$ ；同时，回归误差项服从分布 $a_t|F_{t-1}~N\left(0,{\sigma }_t^2\right)$ 。

预测边界值的估计，与置信区间紧密相关。当置信度水平为 $1-\alpha$ ，样本观察值个数 $n\to \infty$ 时，误差

项 $a_t$ 对应的置信区间为 $a_t\in \left(-t_{\alpha /2}\left(n-2\right){\sigma }_t,t_{\alpha /2}\left(n-2\right){\sigma }_t\right)$ 。例如，如果置信度水平为95%，即 $1-\alpha =95\%$ ，或 $\alpha =5\%$ 时，由于 $\underset{n\to \infty }{\lim }{t}_{\alpha }\left(n-2\right)=1.96$ ，误差项 $a_t$ 的置信区间就为 $a_t\in \left(-1.960{\sigma }_t,1.960{\sigma }_t\right)$ ；如果置信度水平为99%，即 $1-\alpha =99\%$ ，或 $\alpha =1\%$ ，则由于 $\underset{n\to \infty }{\lim }{t}_{\alpha }\left(n-2\right)=2.576$ ，误差项 $a_t$ 的置信区间就为 $a_t\in \left(-2.576{\sigma }_t,2.576{\sigma }_t\right)$ 。有些研究者将置信区间 ${\mu }_t\pm 1.96{\sigma }_t$ 作为时间序列 $r_t$ 在95%置信度水平上的上下

限，例如Wei & Meng (2014) [7] 、Yaziz et al. (2013) [8] 、以及Mathew et al. (2013) [9] 。还有些研究者将置信区间 ${\mu }_t\pm 2.576{\sigma }_t$ 作为时间序列 $r_t$ 在99%置信度水平上的上下限，例如Aradhyula & Holt (1988) [10] 、以及Engle (2001) [11] 。

当GARCH模型被用来解决动态方差问题时，GARCH(1,1)模型使用率很高，例如Zhang、Yang、Li (2013) [12] 、Alberga et al. (2008) [13] 、以及Mohd (2013) [14] ，他们都认为GARCH(1,1)模型可以极大地降低均值估计的绝对误差。不少研究者认为AR-GARCH混合模型对于提高预测模型的精度有极大帮助，例如Tang et al. (2003) [15] 和Garcia et al. (2005) [16] 。

2. 研究模型

假设 $t$ 表示时间变量，当表示离散型时间变量时， $t=0,1,\cdots ,t,\cdots ,T$ ；当表示连续型时间变量时， $t\in \left[0,T\right]$ ，日时间区间为 $\left[t-1,t\right]$ 。假设离散型、连续型时间变量具有同样的意义，今后将不加区别。

假设 $p_t$ 表示金融市场上的股票价格指数， $r_t$ 表示与股票价格指数所对应的股票收益指数，那么，股票收益指数 $r_t$ 将由下式定义：

$r_t=\{\begin{array}{l}\frac{p_t}{p_{t-1}},t=2,\cdots ,t,\cdots ,T\\ 1,t=1;p_1=p_0\end{array}$ (1)

这里，股票收益指数 $r_t$ 是一个时间序列变量。显然，如果 $p_t>p_{t-1}$ ，则 $r_t>1$ ，表示股票价格上涨；如果 $p_t<p_{t-1}$ ，则 $r_t<1$ ，表示股票价格下跌；如果 $p_t=p_{t-1}$ ，则 $r_t=1$ ，表示股票价格不变。股票收益指数 $r_t$ 将围绕曲线 $r_t=1$ 上下波动。

如果股票收益指数 $r_t$ 是一个平稳时间序列，其均值为 ${\mu }_0$ ，方差为 ${\sigma }_0^2$ ，时间变量 $t\in \left[1,\cdots ,T\right]$ ，那么，时间序列 $r_t$ 与其 $k$ 阶滞后序列之间的自协方差可以定义为：

${\gamma }_k=Cov\left(r_t,r_{t-k}\right)=E\left(r_t-{\mu }_0\right)\left(r_{t-k}-{\mu }_0\right)$ (2)

那么，时间序列 $r_t$ 与其 $k$ 阶滞后序列之间的自相关系数可以定义为(Tsay, 2005) [17] ：

${\rho }_k=\frac{{\gamma }_k}{{\gamma }_0}=\frac{Cov\left(r_t,r_{t-k}\right)}{Var\left(r_t\right)}=\frac{E\left(r_t-{\mu }_0\right)\left(r_{t-k}-{\mu }_0\right)}{E{\left(r_t-{\mu }_0\right)}^2}$ (3)

如果零假设条件为 $H_0:{\rho }_1={\rho }_2=\cdots ={\rho }_m=0$ ，表示不存在自相关性；非零备择假设 $H_a:{\rho }_i\ne 0$ ， $i\in \left\{1,2,\cdots ,m\right\}$ ，表示存在自相关性。统计量 $Q\left(m\right)$ 被专门用来检验时间序列 $r_t$ 是否存在自相关性(Ljung & Box,1978) [18] ：

$Q\left(m\right)=T\left(T+2\right){\displaystyle \underset{k=1}{\overset{m}{\sum }}\frac{{\rho }_k^2}{T-k}}$ (4)

如果统计量 $Q\left(m\right)>{\chi }_{\alpha }^2$ ，那么，就拒绝零假设 $H_0:{\rho }_1={\rho }_2=\cdots ={\rho }_m=0$ ，表示存在自相关性。这里： ${\chi }_{\alpha }^2$ 表示 ${\chi }^2$ 分布， $\alpha$ 表示显著性概率水平， $m$ 表示自由度。当使用Eview统计软件进行检验时，统计检验条件 $Q\left(m\right)>{\chi }_{\alpha }^2$ 与显著性概率水平 $p\le \alpha$ 一致，所以，一般地，只要统计量 $Q\left(m\right)$ 检验的概率值小于1%、5%、10%，就可以拒绝假设 $H_0$ 而接受假设 $H_a$ 。

如果股票收益指数 $r_t$ 是一个自相关时间序列，没有单位根，那么，就适合采用自回归(AR)模型作为预测模型。假设AR自回归模型具有形式 $r_t={\mu }_t+a_t$ ，对于滞后阶数 $p$ 的选择，可以根据回归过程按照AIC信息准则选取。其中， ${\mu }_t={\varphi }_0+{\varphi }_1{r}_{t-1}+\cdots +{\varphi }_p{r}_{t-p}$ 表示自相关模型的期望值， $E\left(r_t\right)={\mu }_t$ 。误差项 $a_t$ 具有均值 $E\left(a_t\right)=0$ ，动态方差由GARCH(1,1)确定， $VaR\left(a_t\right)={\sigma }_t^2=\omega +\alpha a_{t-1}^2+\beta {\sigma }_{t-1}^2$ ，且 $a_t={\sigma }_t{\epsilon }_t$ ， ${\epsilon }_t~N\left(0,1\right)$ 。

一般地，为了提高预测精度，大多数人喜欢采用移动平均模型(MA)来处理误差项，为此而采用ARMA模型。由于MA模型无论如何处理，其原始模型的误差项 $a_t$ 并没有改变，所以，我们将试图通过差分模型来提高预测模型的精度。

为了对误差项进行差分处理，需要做一些变换。假设变量 $q_t=F\left(a_t\right)\in \left[0,1\right]$ 表示随机误差变量 $a_t$ 的累积概率函数，它的反函数满足 $a_t=F^{-1}\left(q_t\right)\in \left(-\infty ,+\infty \right)$ 。为了满足概率函数极限值要求，可以定义概率函数为如下形式：

$F\left(x\right)=\frac{1}{1+{\text{e}}^{-x}},\forall x\in \left(-\infty ,\infty \right),\underset{x\to -\infty }{\lim }F\left(x\right)=0,\underset{x\to \infty }{\lim }F\left(x\right)=1,F\left(x\right)\in \left(0,1\right)$ (5)

我们的目的就是要把对于误差项 $a_t$ 的讨论，转化成对于其概率值 $q_t$ 的讨论，从而通过对于概率值 $q_t$ 的差分运算和模型预测，实现提高误差项 $a_t$ 的预测精度的目的。

为了实现对于概率值 $q_t$ 的预测，我们希望求出条件期望值 $E\left(q_t|F_{t-1}\right)$ 。由于概率值 $q_t$ 来自于自回归模型的误差项，它的取值与许多未知因素有关，所以，预测很困难。不同类型的投资者，例如风险厌恶型、风险喜爱型、风险折中型，他们对于条件期望值 $E\left(q_t|F_{t-1}\right)$ 的预测可能低于50%、高于50%、或者等于50%。为了解决这个问题，我们将尝试使用差分方法来处理条件期望值 $E\left(q_t|F_{t-1}\right)$ 。

对于概率变量 $q_t$ ，其一阶差分可以表示为 $d{q}_t=q_t-q_{t-1}$ ，二阶差分可以表示为 $d^2{q}_t=d{q}_t-d{q}_{t-1}$ ，依此类推，n阶差分可以表示为 $d^n{q}_t=d^{n-1}{q}_t-d^{n-1}{q}_{t-1}$ 。如果考虑差分运算的逆运算，就有 $d^{n-1}{q}_t=d^{n-1}{q}_{t-1}+d^n{q}_t$ ，依此类推， $d{q}_t=d{q}_{t-1}+d^2{q}_t$ ， $q_t=q_{t-1}+d{q}_t$ 。所以，按照差分模式，就有一般形式：

$q_t=q_{t-1}+d{q}_{t-1}+d^2{q}_{t-1}+\cdots +d^{n-1}{q}_{t-1}+d^n{q}_t$ (6)

这里，n是差分项最大阶数。以上关系式是一个恒等式，其前n项是已知的，只有最后一项 $d^n{q}_t$ 是未知项。假如未知项 $d^n{q}_t$ 可以用前面的已知项进行预测，即：

$d^n{q}_t={\pi }_t+{\upsilon }_t$ (7)

其中，主要部分 ${\pi }_t$ 可以表示为：

${\pi }_t={\alpha }_0+{\alpha }_{1}d{q}_{t-1}+\cdots +{\alpha }_{n-1}{d}^{n-1}{q}_{t-1}+{\beta }_1{d}^n{q}_{t-1}+{\beta }_2{d}^n{q}_{t-2}+\cdots +{\beta }_l{d}^n{q}_{t-l}$ (8)

所以，概率变量 $q_t$ 可以表示为：

$q_t=q_{t-1}+d{q}_{t-1}+d^2{q}_{t-1}+\cdots +d^{n-1}{q}_{t-1}+{\pi }_t+{\upsilon }_t$ (9)

这里， ${\upsilon }_t$ 是以上回归模型的误差项，l是未知项 $d^n{q}_t$ 的滞后阶数。在实际验证过程中，我们将尝试给l赋予不同的滞后阶数值，来测试l滞后阶数的选取对于预测精度的影响。

如果得到了概率变量 $q_t$ 的预测值 ${q^{\prime }}_t=q_{t-1}+d{q}_{t-1}+d^2{q}_{t-1}+\cdots +d^{n-1}{q}_{t-1}+{\pi }_t$ ，那么，就可以通过下式获得自相关AR模型的误差项 $a_t$ 的预测值 ${a^{\prime }}_t$ ：

${a^{\prime }}_t=F^{-1}\left({q^{\prime }}_t\right)=-\ln \left(\frac{1}{{q^{\prime }}_t}-1\right)$ (10)

这样，再通过AR自相关模型，就可以得到股票收益指数 $r_t$ 的预测值为：

$r_t={\mu }_t+{a^{\prime }}_t+{\eta }_t$ (11)

其中，误差项 ${\eta }_t$ 是比误差项 $a_t$ 更小的一个误差项； ${r^{\prime }}_t={\mu }_t+{a^{\prime }}_t$ 将成为收益指数 $r_t$ 的新预测值。误差项 ${\eta }_t$ 的取值由下式决定：

${\eta }_t=a_t-{a^{\prime }}_t=-\ln \left(\frac{1}{q_t}-1\right)+\ln \left(\frac{1}{{q^{\prime }}_t}-1\right)=\ln \frac{q_t\left(1+{q^{\prime }}_t\right)}{{q^{\prime }}_t\left(1+q_t\right)}$ (12)

关于预测模型精度的测量，主要采用以下三种测试形式。假设变量 $r_t$ 表示实际股票收益指数， ${r^{\prime }}_t$ 表示股票收益指数的预测值，那么，我们主要采用以下三种测试值来测量预测的精度。

1) 样本相关系数值(Corr)。一般来说，因为相关系数是表现自变量和因变量之间相关依赖关系的主要参数，回归系数 $R$ 的平方值往往被用来测定预测模型的绩效(Ferreira & Pedro, 2011) [19] 。预测值与实际值之间的契合程度，通常用他们之间是否具有最小预测误差值、或者最高相关系数值来决定(Alexander, 2008II) [20] 。

$Corr\left(r_t,\stackrel{⌢}{r}\right)=\frac{{\displaystyle \underset{t=1}{\overset{T}{\sum }}\left(r_t-{\bar{r}}_t\right)\left({r^{\prime }}_t-{{\bar{r}}^{\prime }}_t\right)}}{\sqrt{{\displaystyle \underset{t=1}{\overset{T}{\sum }}{\left(r_t-{\bar{r}}_t\right)}^2}}\sqrt{{\displaystyle \underset{t=1}{\overset{T}{\sum }}{\left({r^{\prime }}_t-{{\bar{r}}^{\prime }}_t\right)}^2}}}$ (13)

2) 误差平均值(RMSE)。它可以用误差平方值的均值开方而得到，能够很好地判断预测模型(Assis et al., 2010) [21] 。

$RMSE=\sqrt{\frac{1}{T}{\displaystyle \underset{t=1}{\overset{T}{\sum }}{\left(r_t-{r^{\prime }}_t\right)}^2}}$ (14)

3) 涨跌命中率(Hit Ratio)，用具有相同符号值的样本个数除以样本总数得到。

$\text{Hit}\text{Ratio}=\frac{\text{Number}\text{of}\text{correct}\text{signs}}{\text{Total}\text{number}\text{of}\text{predictions}}$ (15)

如果预测的目的仅仅是简单地预测金融市场资产的价格，那么，对于投资者来说，决策的有效性就会受到限制(Zhang, Pan, Chen, 2013) [22] ，因为对于大多数投资者来说，预测价格发展的涨、跌趋势，比预测价格相比于实际值的接近程度更有意义。涨跌命中率(Hit Ratio)是一种简单而有效的方法(Sonono & Mashele, 2015) [23] 。

3. 数据的单位根及自相关性检验

本文所引用的样本数据是由中证指数提供的沪深300股票指数每日收盘价，样本数据下载自万得数据库。时间区间以日为单位，介于2002年1月4日至2017年4月10日之间，共有3699个样本。所有运算均通过Eviews 8.0统计软件进行。

假设 $p_t$ 表示沪深300价格指数， $r_t$ 表示沪深300价格指数的收益指数。

表1为两个变量在AIC信息准则下的ADF单位根检验结果，容易发现在1%、5%、10%等三种概率水平下，三种模型都表明沪深300价格指数变量 $p_t$ 的单位根检验都未通过，即水平变量为非稳定；相反地，在1%、5%、10%等三种概率水平下，沪深300收益指数变量 $r_t$ 的单位根检验在模型3和模型2下都获得通过，即水平变量为稳定。鉴于此，本文中的分析数据将基于变量 $r_t$ 进行。

表2展现了沪深300收益指数 $r_t$ 的Ljung-Box统计量(Ljung & Box, 1978)自相关性检验结果。可以看出，在10%水平下， $r_t$ 与 $r_{t-1}$ 之间的自相关系数为 ${\rho }_1=0.028$ ；在1%水平下，自相关系书 ${\rho }_{10}=0.002$ ， ${\rho }_{20}=0.015$ ， ${\rho }_{30}=-0.025$ 。显然，沪深300收益指数 $r_t$ 是一个具有自相关性的时间序列，适合采用AR自相关模型进行回归预测。

4. 实证分析

4.1. AR(4)预测模型

因为沪深300收益指数 $r_t$ 是一个没有单位根的自相关时间序列，适合采用AR自相关模型 $r_t={\mu }_t+a_t$ ，建立预测方程。通过对比有关自相关模型，选择出以下AR(4)模型：

${\mu }_t=\underset{t=28.32,p=0.0000}{0.917730}+\underset{t=-1.70,p=0.0883}{0.028012}{r}_{t-1}-\underset{t=-1.57,p=0.1158}{0.025854}{r}_{t-2}+\underset{t=1.32,p=0.1881}{0.021632}{r}_{t-3}+\underset{t=3.58,p=0.0003}{0.058871}{r}_{t-4}$ (16)

$R^2=0.0055,S.E.=0.0173,AIC=-5.2684,SIC=-5.2600$ (17)

Table 1. ADF unit root test with AIC criterion for Hushen300 index and its return index

表1. 沪深300指数及其收益指数在AIC准则下的ADF单位根检验

备注：1) 以上检验最大滞后阶数为29；2) ADF检验模型3既包含趋势项又包含截距项，模型2仅包含截距项，模型1既不包含趋势项又不包含截距项；3) SIC、HIC信息准则结果与AIC一致。

Table 2. Autocorrelation test for Hushen300 return index

表2. 沪深300收益指数自相关性检验

备注：AC表示自相关系数，Q表示Ljung-Box统计量，P表示 ${\chi }^2$ 检验概率，括号中的数字为滞后阶数。

显然，AR(4)模型具有一个很小的可决系数 $R^2=0.0055$ ；所以，当定义 $a_t=r_t-{\mu }_t$ 时，相关系数 $corr\left(r_t,a_t\right)=0.9972$ ，表示误差项 $a_t$ 可能包含了太多有关收益指数 $r_t$ 的信息，主要应该是宏观经济冲击信息、企业运行私人信息、以及其它未知信息。这个时候，如果仅仅用 $E\left(r_t\right)={\mu }_t$ 来预测收益指数 $r_t$ 的值，则误差会很大。

4.2. GARCH(1,1)模型

对于误差项 $a_t$ ，一般自回归条件异方差模型GARCH(1,1)可以表示为：

${\sigma }_t^2=\underset{t=4.65,p=0.0000}{1.46E-06}+\underset{t=14.5,p=0.0000}{0.064224}{a}_{t-1}^2+\underset{t=202.0,p=0.0000}{0.933380}{\sigma }_{t-1}^2,a_t={\sigma }_t{\epsilon }_t$ (18)

$LL=6826.048,AIC=-3.689,SIC=-3.584,HIC=-3.687$ (19)

这里，静态方差 ${\bar{\sigma }}^2=0.000609$ ，ARCH项系数为 $\alpha =0.064224>0$ ，GARCH项系数为 $\beta =0.933380>0$ ，截距项是 $\omega =0.00000365>0$ ，三个参数之间具有关系 $\alpha +\beta =0.99760400<1$ ， $\omega +\alpha +\beta =0.99760546<1$ 。由于GARCH项系数为 $\beta$ 值较大，说明条件异方差的聚集效应明显。

如果置信度水平为99%，即 $1-\alpha =99\%$ ，或 $\alpha =1\%$ ，那么，收益指数 $r_t$ 的置信区间就为 $r_t\in \left({\mu }_t-2.576{\sigma }_t,{\mu }_t+2.576{\sigma }_t\right)$ 。

4.3. 差分预测结果

表3列出了沪深300收益指数的AR(4)模型误差项 $a_t$ 经过转换后的水平变量 $q_t$ 、一阶差分 $d{q}_t$ 、二阶差分 $d^2{q}_t$ 的自相关性检验结果。在开展自相惯性检验之前，ADF检验发现，在3种模型之下，AIC信息准则表明，变量 $q_t$ 、一阶差分 $d{q}_t$ 、二阶差分 $d^2{q}_t$ 序列都是平稳序列，都不存在单位根。

可以看出，水平变量 $q_t$ 的自相关性很弱， $AC\left(1\right)=0.000$ ，说明变量 $q_t$ 与其一阶滞后变量 $q_{t-1}$ 之间几乎不存在自相关性。对于一阶差分时间序列 $d{q}_t$ ， $AC\left(1\right)=-0.501$ ，表明变量 $d{q}_t$ 与其滞后一阶变量 $d{q}_{t-1}$ 之间具有明显自相关性。对于二阶差分时间序列 $d^2{q}_t$ ， $AC\left(1\right)=-0.668$ ，表明变量 $d^2{q}_t$ 与其滞后一阶变量 $d^2{q}_{t-1}$ 之间具有明显自相关性。

由于变量 $q_t$ 的一阶差分时间序列 $d{q}_t$ 和二阶差分时间序列 $d^2{q}_t$ 与它们各自的高阶滞后差分序列之间都具有明显自相关性，所以，可以对一阶和二阶差分序列建立自相关模型。为了简单起见，我们选择建立二阶差分时间序列 $d^2{q}_t$ 的预测模型。一般形式如下：

$d^2{q}_t={\pi }_t+{\upsilon }_t$ , ${\pi }_t={\alpha }_0+{\alpha }_{1}d{q}_{t-1}+{\displaystyle \underset{i=1}{\overset{l}{\sum }}{\beta }_i{d}^2{q}_{t-i}}$ (20)

$q_t={q^{\prime }}_t+{\upsilon }_t$ , ${q^{\prime }}_t=q_{t-1}+d{q}_{t-1}+{\pi }_t$ (21)

$r_t={{\mu }^{\prime }}_t+{\eta }_t$ , ${{\mu }^{\prime }}_t={\mu }_t-\ln \left(\frac{1}{{q^{\prime }}_t}-1\right)$ , ${\eta }_t=\ln \frac{q_t\left(1+{q^{\prime }}_t\right)}{{q^{\prime }}_t\left(1+q_t\right)}$ (22)

从沪深300收益率指数的自回归模型 $r_t={\mu }_t+a_t$ 的误差项 $a_t$ 出发，经过转换，就可以得到其概率函数 $q_t$ ；然后对 $q_t$ 的二阶差分序列按照回归模型 $d^2{q}_t={\pi }_t+{\upsilon }_t$ 进行估计，得到二阶差分时间序列 $d^2{q}_t$ 的预测值 ${\pi }_t$ ；在此基础上，按照模型 ${q^{\prime }}_t=q_{t-1}+d{q}_{t-1}+{\pi }_t$ 得到 $q_t$ 的预测值 ${q^{\prime }}_t$ ；最终得到 $r_t$ 的 $l$ 阶差分预测值 ${{\mu }^{\prime }}_t$ ；相应地，得到新的误差项 ${\eta }_t$ 。

表4列出了有关运算结果。

在建立二阶差分项预测模型 $d^2{q}_t={\pi }_t+{\upsilon }_t$ 时，分别选取滞后阶数为1、50、100、150、200、300、400、500、600、700等10种情况建立回归模型。

Table 3. Autocorrelation tests for transferred residual items of Hushen300 return index in level, first and second orders

表3. 沪深300收益指数误差项经过转换后的水平、一阶、二阶差分项的自相关性检验

备注：AC表示自相关系数，Q表示Ljung-Box统计量，P表示 ${\chi }^2$ 检验概率，括号中的数字为滞后阶数。

Table 4. Relations between the forecasting results and related variables for AR and difference models of Hushen300 return index

表4. 沪深300收益指数AR模型和差分模型的有关预测结果以及相关变量之间的关系

从表4中，我们可以看出，通过应用AR-差分预测模型，可以得到如下结果：

二阶差分项预测模型 $d^2{q}_t={\pi }_t+{\upsilon }_t$ 的可决系数 $R^2$ 的值都很高，从0.8336逐渐上升到0.8698；同时，二阶差分项的实际值与其预测值之间的相关系数 $\rho \left(d^2{q}_t,{\pi }_t\right)$ 的值也随着滞后阶数的升高增大。这说明模型中变量之间的整体依赖性较高，对二阶差分项的预测具有一定意义。

图1列出了沪深300收益指数 $r_t$ 、AR模型预测值 ${\mu }_t$ 、以及在滞后阶数等于700时的AR-差分模型预测值 ${{\mu }_t|}_{l=700}$ 的曲线图示(只列出了2005年以后的值)。可以看出，AR-差分模型预测曲线比单纯AR模型预测曲线更接近表现实际收益指数的发展趋势。

图2列出了沪深300收益指数 $r_t$ 、以及在概率水平为99%时的下限 ${\mu }_t-2.576{\sigma }_t$ 和上限 ${\mu }_t+2.576{\sigma }_t$ 。从这里可以看出，简单的GARCH模型只能界定收益指数曲线的上下边界，但不能提高预测的精度。

Figure 1. Curves of Hushen300 return index, forecasting values of pure AR model, forecasting values of AR-difference model with 700-order lag items

图1. 沪深300收益指数、单纯AR模型预测值、以及在滞后阶数等于700时的AR-差分模型预测值曲线图示

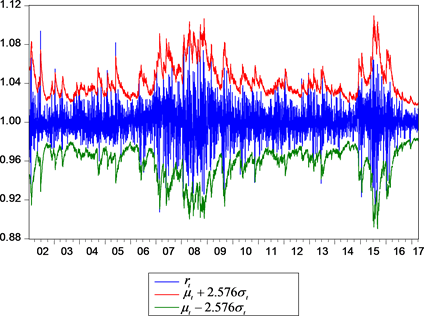
Figure 2. Curves of Hushen300 index, upper limit value and lower limit value under the significant probability level of 99%

图2. 沪深300收益指数、以及在显著概率水平为99%时的下限值和上限值曲线图示

4.4. 差分预测精度提升测量

第一，相关性测量。

在表4中，沪深300收益指数与AR-差分模型的预测值之间的相关系数 $\rho \left(r_t,{{\mu }^{\prime }}_t\right)$ 的值，都随着滞后阶数 $l$ 的增大而增大，从0.0815，逐渐增大到0.4758，并且都大于沪深300收益指数与单纯AR模型的预测值之间的相关系数 $\rho \left(r_t,{\mu }_t\right)$ 的值0.0816。这表明：AR-差分模型提高了预测值与实际值之间的相关性，从趋势变化关系上与实际值更趋于一致。

与此同时，单纯AR模型预测值与差分模型预测值之间的相关系数 $\rho \left({\mu }_t,{{\mu }^{\prime }}_t\right)$ 的值也在逐渐减小，这也从另外一个侧面反映了差分模型预测值远离单纯AR模型预测值而接近实际值的情况。

第二，误差平均值(RMSE)测量。

在表4中，单纯AR模型预测值与收益指数实际值之间的误差平均值RMSE的值是0.018111；而AR-差分模型预测值与收益指数实际值之间的误差平均值RMSE的值在滞后阶数大于1之后，都小于0.018111，而且随着滞后阶数的提高越来越小。

同时，AR-差分预测所得到的误差项的平均值 ${\bar{\eta }}_t$ 明显比单纯AR模型所得到的误差项平均值 ${\bar{a}}_t$ 要小很多，其绝对值对比，在 $l=1$ 时 ${\bar{a}}_t$ 的绝对值是 ${\bar{\eta }}_t$ 的绝对值的44倍以上，在 $l=700$ 时 ${\bar{a}}_t$ 的绝对值是 ${\bar{\eta }}_t$ 的绝对值的4.5倍以上。

另外，沪深300收益指数与预测模型误差项之间得相关系数 $\rho \left(r_t,{\eta }_t\right)$ 的值也随着滞后阶数的增大而减小。

这些结果都表明，由于引进差分方法，对沪深300收益指数进行预测时预测模型的误差项值明显降低了；反之则表明对于收益指数 $r_t$ 的预测精度明显提高了。

第三，预测成功率测量。

表5列出了在单纯AR模型和AR-差分模型下沪深300收益指数实际值与预测值之间的命中率测试结果。分四种情况：

情况1：当沪深300收益指数实际值为上涨、并且预测值也为上涨时， $\left\{r_t\ge 1\right\}\cap \left\{\chi \ge 1\right\}$ ，预测样本数占比最低为31.64%，最高为35.67%。滞后阶数的变化，对于同时上涨情况在中国股市上的预测效率来说影响不大；尽管如此，随着滞后阶数的提高，预测样本数占比变化并没有持续变小，而是逐渐变大，并且占比基本稳定在31%至35%之间。这种情况下，AR-差分模型预测能力与单纯AR模型相当。

情况2：当沪深300收益指数实际值为上涨、而预测值为下降时， $\left\{r_t\ge 1\right\}\cap \left\{\chi <1\right\}$ ，预测样本数占比最低为17.04%，最高为21.17%；随着滞后阶数的提高，预测样本数占比的变化很微弱，基本稳定在17%至21%之间。这种情况下，AR-差分模型预测能力比单纯AR模型稍弱。

Table 5. Results of consistent test between the real value and forecasting value for Hushen300 return index under the both situations of pure AR model and AR-difference model

表5. 在单纯AR模型和AR-差分模型下沪深300收益指数实际值与预测值之间一致性测试结果

备注：1) 变量 $\chi$ 表示预测值，其中： ${\mu }_t$ 表示单纯AR模型预测值， ${{\mu }^{\prime }}_t$ 表示AR-差分模型预测值；2) 由于二阶差分模型的预测阶数不同，所以，每个预测模型的样本个数都不一样；3) 符号 $\cap$ 表示且运算或交运算。

情况3：当沪深300收益指数实际值为下跌、并且预测值也为下跌时， $\left\{r_t<1\right\}\cap \left\{\chi <1\right\}$ ，随着滞后阶数不断提高，预测样本数占比从最低15.17%逐渐提高到27.56%，不断提高。这种情况下，AR-差分模型预测能力明显高于单纯AR模型。

情况4：当沪深300收益指数实际值为下跌、而预测值为上涨时， $\left\{r_t<1\right\}\cap \left\{\chi \ge 1\right\}$ ，随着滞后阶数不断提高，预测样本数占比从最高32.12%逐渐降低到18.78%，降幅非常明显。这种情况下，AR-差分模型预测能力明显高于单纯AR模型。

情况1 + 情况3：情况1与情况3表现了沪深300收益指数实际值与预测值同涨、或者同降的两种趋同情形，其样本数占比反映了预测值与实际值运行方向完全相同的情况，准确地反映了预测值在涨跌趋势上的准确性，所以，样本数占比值越高越好。很明显，随着滞后阶数的提高，样本数占比也从50.84%增长到62.65%；与单纯AR模型下的50.99%相比，高了11.66%。这种情况下，AR-差分模型预测能力明显高于单纯AR模型。这说明趋势预测完全成功的概率最高可达到62.65%；而完全失败的概率为37.35%，明显小于成功的概率。总体来说，AR-差分模型预测能力明显高于单纯AR模型。

5. 小结及今后研究方向

本文一开始，首先对具有自相关性的经济时间序列的预测模型进行了梳理，指出：AR自相关模型比较适合对于具有自相关性的单变量时间序列进行建模分析，VAR向量自相关模型比较适合对于具有自相关性的多变量时间序列进行建模分析；ARIMA自相关协整移动平均模型比较适合对于具有非稳定初始状态的时间序列进行建模分析；ARMA自相关移动平均模型比较适合对于具有稳定初始状态的时间序列进行建模分析；MA移动平均模型比较适合对于AR模型的误差项进行移动平均建模分析。

虽然AR、ARIMA、ARMA、MA模型都被经常用来进行预测，但是，在实践中，由于人们对于误差项的处理没有太好的办法，所以在进行预测时，常常将误差项作为零被扔掉了，这样预测的精度也就大受影响。因为回归模型的误差项通常包含了几乎所有来自私人的信息、来自宏观经济的冲击信息、以及来自某些未知源的信息，所以，当回归模型的误差项被简单地忽略掉时，预测模型的精确性将受到很大的影响。

那么，如何考虑误差项，才能够提高预测精度呢？由于AR自相关模型的误差是AR、ARIMA、ARMA、MA等模型的基础误差，所以，本文重点就是通过对AR模型误差的转换，并通过差分模型，来提高预测的精度。具体做法是：先建立时间序列的AR自回归模型，得到误差项；然后对该误差项通过一个概率函数将其转换为一个(0,1)之间的概率值；再对该概率值序列建立一阶和二阶差分序列；通过对二阶差分序列的预测实现对于概率值序列的预测；将预测所得到的概率预测值通过概率函数的逆函数转换成误差值的预测值；将该误差值的预测值代入AR自回归模型，得到新的预测值，这就是AR-差分模型所得到的预测值。

通过对沪深300指数的增长率指数进行实证分析表明：

第一，相关性分析表明：AR-差分模型提高了预测值与实际值之间的相关性，从趋势变化关系上与实际值更趋于一致。

第二，RMSE误差平均值分析表明：AR-差分模型大大提高了对沪深300收益指数的预测精度，平均误差大大减小。

第三，趋势一致性分析表明：AR-差分模型预测能力明显高于单纯AR模型，AR-差分模型趋势预测完全成功的概率最高可达到62.65%；而完全失败的概率仅为37.35%。

由于我们使用这种方法也研究过美国道琼斯指数，发现对于双涨即情况1来说，AR-差分模型预测能力明显高于单纯AR模型；但是，本文对于沪深300指数的研究，发现对于双降即情况3来说，AR-差分模型预测能力明显高于单纯AR模型。我们认为，出现这种差异的主要原因是自2008年金融危机之后，中国股票市场持续低迷时间较长，而美国股市却有了比较稳定的回升。因此，对于低迷股市，趋势的双降预测准确率更高；而对于增长型股市，趋势的双涨预测准确率更高。这种猜测，今后还需要用更多实证检验去证明。

致谢

感谢匿名审稿人对初稿的褒奖评价及大力推荐。