基于非量测相片的三维模型重建

Three-Dimensional Model Reconstruction Based on Non-Measured Photo

摘要: 随着科技的发展，对视觉感受的要求提高，越来越多的三维影像产品进入生活，然而三维模型重建受到诸多限制，并未达到公众要求。近年来，用非量测相片进行三维重建成为三维模型重建的流行方式之一。本文主要介绍了使用非量测相片进行相机标定、特征点提取与匹配、极线约束与本征矩阵计算、三维重建、误差分析，最终完成三维模型重建的过程，并简要分析了此方法的应用前景。

Abstract: With the development of science, the requirement of visual feeling is improved, an increasing number of three-dimensional image products enter life. Nevertheless, the three-dimensional model reconstruction is subject to many restrictions, and does not meet the public requirement. In recent years, three-dimensional reconstruction with non-measurement photos has become one of the popular ways of 3D model reconstruction. This paper mainly introduces the process of 3D model reconstruction, including the use of non-measurement photos for camera calibration, extraction and matching of feature points, line constraint and intrinsic matrix calculation, three-dimensional reconstruction, error analysis. Lastly, the paper briefly analyzes the prospect of this method.

1. 引言

随着地球数字化、信息化、智能化的发展，快速将物体的原态呈现出来，建立物体的三维模型成为当前的研究热点。目前，已有的三维模型重建方法由于效率低、周期长、成本高、受限大，而不能广泛服务日常生活，如利用三维激光扫描技术进行三维重建和传统的室内三维重建。近年来，数码摄像产品性价比进一步提高得到广泛使用且其数码摄像技术有了突破性进展，摄影成像的质量和分辨率有了大幅度的提高，为三维模型构建提供了广阔的发展空间 [1] 。因此，基于非量测相机进行三维模型重建应运而生。基于非量测相片的三维模型重建方法只需一部普通的智能手机或CCD数码相机，在不同的角度拍摄得到多张相片，即可进行物体的三维构建，是三维重建的又一进步。此方法成本低廉，自动化程度高，实用性好，室内外均可实现三维重建，受到学者的广泛重视，并应用到众多领域。本文概括介绍了基于非量测相片进行三维重建的各阶段算法及整体流程。

2. 基于相片的三维几何信息计算方法

通过二维相片进行目标物体三维几何信息的获取，是摄影测量以及计算机视觉等领域的主要研究内容 [2] ，也是三维模型重建的第一步。摄影获得的相片质量越高，三维重建效果越好。实现目标物体三维几何信息的获取过程包括相机内外参数的标定、特征点提取和匹配、极线约束与本征矩阵提取等几个方面。

2.1. 相机标定

在双目立体视觉系统中利用具有不同视角的两幅图像提取获得物体的三维几何信息，是相机标定时必不可少的一步。根据一组已知其世界坐标系坐标和图像平面像素坐标系坐标的对应点来确定相机的内部和外部参数，称为相机标定 [3] 。相机标定有三种不同形式，包括相片传统标定方法、基于主动视觉的相机标定方法和相机自标定方法 [4] 。

相机标定可用棋盘图片作为标定模板，再用待标定的摄像头在不同视角下拍摄获得棋盘图片，将这些图片用OpenCV自编写程序或Matlab Camera Calibration Toolbox处理，即可计算出待标定摄像头的内参以及每一幅图像相对应的外部参数。

2.1.1. 坐标系转换

在利用非量测相片进行三维模型重建的过程中，主要涉及两种类型坐标系，一类是世界坐标系，另一类是相机坐标系，这两类坐标系均属于右手坐标系统。相片坐标投影变换过程如下。

首先，将目标点的世界坐标系坐标转换为相机坐标系坐标，变换过程中涉及到坐标点的平移和旋转，可得到旋转矩阵 $R$ 和平移矩阵 $T$ ；然后，将目标点变换得到的相机坐标再转换为像平面坐标；再然后，根据目标点的像平面坐标与实际投影之间的误差，建立透镜畸变模型，实现像平面坐标点转换实际投影点(相机捕捉到的点)过程；最后，完成将目标点的像平面坐标转换成为像素坐标。

2.1.2. 内参提取

假设相机坐标系与世界坐标系重合，空间中有一目标点P，则其空间坐标为 $\left(X,Y,Z\right)$ 。该目标点在像面上的像为点p，其像素坐标为 $\left(x,y\right)$ 。目标点的光心在图像上对应的像素坐标为 $\left(c_x,c_y\right)$ ，则有公式(1)如下

$Z\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=\left[\begin{array}{ccc}f& 0& c_x\\ 0& f& c_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}X\\ Y\\ Z\end{array}\right]$ (1)

上式中的 $3\times 3$ 阶矩阵 $K$ 称为内参矩阵，只与相机的内部参数有关。

2.1.3. 外参提取

现实中，目标点的相机坐标系与世界坐标系在无特殊情况下是不一致的，因此，世界坐标系下的目标点P要投影到像面坐标系下时，先要将非量测相片中提取的特征点的世界坐标转换到相机坐标系下。设目标点P的世界坐标为 $X$ ，其到摄影相片光心的垂线距离大小为s(相当于 $Z$ )，目标点P的像面坐标设为 $x$ 。将 $R$ 设为相机坐标系与世界坐标系之间的相对旋转矩阵，向量 $T$ 设为目标点在两坐标系之间的相对位移，则有公式(2)如下

$sx=K\left[\begin{array}{cc}R& T\end{array}\right]\left[\begin{array}{c}X\\ 1\end{array}\right]$ (2)

其中由相对旋转矩阵 $R$ 与相对位移向量 $T$ 组合而成的矩阵 $\left[\begin{array}{cc}R& T\end{array}\right]$ ，称为外参矩阵。外参矩阵不受相机的内部参数影响，只与世界坐标系中相机的空间位置相关。

2.2. 特征点提取与匹配

用两幅非量测相片中提取的对应特征点求取两相机位置的相对关系，就是解决相片特征点的提取与匹配的问题。常用的特征点检测方法包括SIFT特征点检测、SURF特征点检测和Harris特征点检测。Harri特征点检测对旋转，尺度及光照比较敏感，SIFT特征提取方法的优点是鲁棒性好，对图像的旋转变换、尺度变换和光照等具有不变性；然而，SIFT特征提取方法的缺点是速度较慢，不适合动目标图像的实时处理。当两张相片的差别较大时，可以使用SIFT特征提取函数算法；相片之间差别不大时，可以使用提取特征点更快速的算法，如SURF、ORB等。

特征点提取与匹配可用OpenCV函数库中的函数算法实现，其过程可描述为：首先，根据需要选择函数算法SiftFeatureDetector (或SurfFeatureDetector)检测特征点，再使用SiftSurfDescriptorExtractor或DescriptorExtractor计算特征点的特征向量，最后采用BruteForceMatcher暴力匹配法或者FlannBasedMatcher选择性匹配法来进行特征点匹配。

2.3. 极线约束与本征矩阵

设点P为世界坐标系中的一点，其坐标表示为 $X$ ，在相片1中的像平面坐标表示为 $x_1$ ，在相片2中的像平面坐标表示为 $x_2$ (注意这两张相片是由一个相机拍摄而成，内部参数矩阵均为 $K$ )，两个相机位置的像平面与目标点P世界坐标 $X$ 之间的垂直距离分别表示为 $s_1$ 和 $s_2$ ，经一系列数学推导计算可得

$0={x^{\prime }}_{2}E{x^{\prime }}_1$ (3)

其中

$\begin{array}{l}{x^{\prime }}_1=K^{-1}{x}_1\\ {x^{\prime }}_2=K^{-1}{x}_2\\ E={\stackrel{⌢}{T}}_2{R}_2\end{array}$ (4)

观察上式可以得出，(3)式表示同一目标点在两张相片中的像平面坐标所满足的相互关系，称为极线约束，其中，矩阵 $E$ 称为相片间的本征矩阵。通过两张相片中提取得到的数个对应特征点(5对以上)，则可以利用式(3)解算获取本征矩阵 $E$ 。同时，可以用OpenCV中的特征点的提取和匹配算法从 $E$ 中分解出两个相机的相对变换关系(即 $T$ 和 $R$ )。

3. 三维重建方法

3.1. 双目重建

现在有每对匹配点的坐标，且已知两相片间的变换矩阵。通过已知数据进行三维重建，还原匹配点的空间坐标，有下式

$s{x}_2=K\left(RX+T\right)$ (5)

这个等式中有两个未知量，分别是 $s$ 和 $X$ 。

整理得到一个关于空间坐标X的线性方程

$\stackrel{⌢}{x}K\left[\begin{array}{cc}R& T\end{array}\right]\left[\begin{array}{c}X\\ 1\end{array}\right]=0$ (6)

用SVD求 $X$ 左边矩阵的零空间，再将最后一个元素归一化到1，即可求得 $X$ 。OpenCV提供了该算法，可以直接使用。双目重建利用一个相机在空间中不同角度拍摄获取非量测相片，在重建过程中，由于一些三维信息因投影而丢失了，使得重建结果不够完整 [5] ，因此，还要进行多目重建。

3.2. 多目重建

OpenCV中拥有solvePnP和solvePnPRansac函数，只需知道空间中部分点的坐标和其对应点的像素坐标，就可以通过solvePnP计算获得相机的空间坐标。进行多目重建的过程原理是首先对最初的两张相片进行双目重建，获得了空间中的一些点，然后加入第三张相片，令此相片与第二张相片进行特征点的匹配，在形成的匹配点中包含相片二与相片一之间的部分匹配点，同时在第三张相片中这些点的像素坐标已知，即可通过solvePnP得到第三个相机的空间位置，得到相机三到相机一的变换矩阵。

通过以上方法得到相机三的变换矩阵后，就可以使用triangulatePoints算法将相片三和相片二之间的匹配点进行三角化处理，得到相片三的空间位置坐标，然后将其融合入之前的三维点云。之前已有的空间点，不必再添加进去，只将相片二和相片三之间新匹配得到的点添加进三维点云，重复进行。其大体流程如图1所示。

4. 实验与分析

4.1. 数据准备

进行三维重建相片采集前必须对相应的数码设备进行相机检校 [6] 。然后使用手机或数码相机对目标物体按要求进行拍照；即目标物体与摄像头像平面之间的夹角控制在45度以下，对目标物体的姿势与位置进行对角度拍摄(最好全方位360˚)，进行目标物体拍摄时注意照片之间的交叠面积，注意摄像头分辨

率的设置。相片质量对相机内外参数提取精度十分重要。本文使用手机对目标物体水杯进行拍摄，拍摄有80张相片。相片样品如图2所示。

将拍摄得到所有相片导入SFM进行点云的处理。首先进行相片特征点的提取与匹配。由于手机拍摄的相片的不稳定因素多且误差大，而基于SURF的特征点检测方法具有良好的提取精度和鲁棒性，又加快了速度，且应用广泛。因此，本文特征点的提取使用的是SURT函数。然后使用OpenCV中的FlannBasedMatcher进行特征点的匹配。影像匹配 [7] [8] 可以适当借鉴全景影像的研究，有利于研究进展。

根据所得的匹配结果，利用射影定理得到相机的位置信息称稀疏重建。稀疏重建过程使用了PnP函数，而Lepetit和Moreno提出的透视成像摄像机高精度快速位姿估计算法EPnP (Efficient Perspective-n-point)效率和鲁棒性都得到了提高 [9] ，可得到较好的重建效果。结果的衡量标准常用基于Lecenberg-Marquardt算法的Bundler。进行稀疏重建的结果如图3所示。

稀疏重建得到了相机的位置信息，然后根据场景信息与原始照片，得到目标物体水杯的3D点云信息，即密集重建过程。密集重建运用多视立体重建(Multi-view Stereo Reconstruction)得到3D点云。处理图像精度的重建精度、执行效率和完整性对点云质量有影响，目前使用的算法有CMVS和PMVS，而本实验所用的密集重建方法为CMVS。密集重建的结果是一系列点云，三维重建结果可用其他三维建模软件进行显示，进行表面纹理贴图，目前常用的算法是泊松表面重建算法。

4.2. 三维重建结果

将拍摄的所有相片进行特征点提取与匹配，然后三维重建。拍摄照片的数量，拍摄时的稳定程度和角度，目标物体周围环境都会对三维建模的结果产生影响。本实验将三维重建结果的点云图用MeshLab软件进行显示，结果如图4所示。

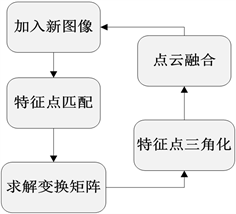
Figure 1. Flow chart of multi-purpose reconstruction

图1. 多目重建流程图

Figure 2. Two-dimensional non-measuring photo

图2. 二维非量测相片

Figure 3. Sparse reconstruction

图3. 稀疏重建

Figure 4. 3D reconstruction of the image

图4. 三维重建图像

在MeshLab软件中，可以对重建的三维点云图进行贴图渲染等操作，进而得到视觉效果较好的三维图像。

理想情况下，三维重建模型应与真实目标物形状、大小等一致或成比例，但在实际操作过程中，由于数据源、构建方法等各种问题，会出现一定的差异 [10] 。将三维重建的结果图与实物进行对比，可知此实验结果有诸多“粗差”点，使三维重建结果显示比较混乱，这与相机拍摄的标准与质量有莫大的关系，且与处理过程使用的函数算法有关。目前三维重建技术还处于初级发展，而精度的提高是三维建模重中之重。此外，目前复杂物体的三维重建只是显示物体的本貌，并不能智能显示目标物体的具体地理位置、尺寸大小等属性信息。

5. 结束语

基于非量测相片的三维重建可谓是新起之秀，此方法自动化高，可操作性强，适用范围广，但是算法复杂，精度低，无成型的智能软件。基于该方式的三维模型重建具有很高的实用性，可用于古文物保护、工艺品生产、工业零件检测等多领域，应用前景广阔。本文通过系统性介绍三维重建过程，并进行了实验，表明此方法可行，且对目标物体的三维重建效果好。

基金项目

淮海工学院科研基金项目，基于地基干涉雷达的变形监测方法研究(项目编号：Z2016015)。江苏省高等学校自然科学研究面上项目，基于InSAR技术的江苏滨海滩涂沉降及侵蚀研究。