1. 引言
许多机械、航空航天等工程结构都可以简化为悬臂梁结构模型,如机器人柔性机械臂、卫星天线、压电能源采集器、飞机的机翼、叶轮机和涡轮发动机叶片、直升机旋翼以及太阳能帆板等。随着科学技术的发展,现代工程结构向大型、高速、轻结构等方向发展。因此,研究悬臂结构的非线性动力学性质具有重大意义。
悬臂梁的非线性动力学控制方程大多是多个非线性项耦合的高阶非线性偏微分方程(组),众所周知对于大多数的偏微分方程是很难求出精确解的,尤其是非线性的。由于实际的需要,必须采用近似方法。中外学者采用各种近似方法对悬臂梁结构的非线性动力学性质作了大量的研究。Nayfeh和Pai用Galerkin方法和多尺度方法 [1] 分析不可伸长悬臂梁的非线性平面和非平面振动响应,发现了几何非线性项产生硬特性,而且它还是非平面响应产生的主要因素。冯景 [2] 考虑水平轴风力发电机的叶片在旋转过程中所受的的气动力,变转速,弹性力和惯性力的综合作用,综合利用Galerkin离散和多尺度方法对悬臂梁的动力学模型进行摄动分析,针对平均方程进行数值模拟,研究了旋转叶片的非线性振动问题。王凤霞 [3] 对平面运动和非平面运动两种柔性悬臂梁的非线性振动以及全局动力学进行了研究,综合利用Galerkin离散和多尺度方法对悬臂梁的动力学模型进行了摄动分析,在平均方程的基础上,得到系统的规范型,运用全局摄动法对系统进行全局动力学分析。Dwivedy和Kar用多尺度方法 [4] 分析了带有质量块的参数激励作用下悬臂梁的周期、概周期和混沌响应。Young和Juan采用Ritz-Galerkin [5] 方法对控制方程离散求解研究了自由端受随机载荷的颤动悬臂梁的非线性响应。Yao和Zhang研究了 [6] [7] [8] 悬臂梁的非线性非平面振荡的多脉冲Shilnikov轨道和混沌动力学行为。他们运用规范型理论将推导的悬臂梁系统的平均方程转化为一个包含最初的拓扑结构的简单形式。然后他们运用能量相位法分析了非线性非平面振动的悬臂梁的全局分叉和混沌动力学行为。Nili Ahmadabadi和Khadem用 [9] 伽辽金方法研究了非线性能量阱对受冲击激励的悬臂梁的非线性振动控制的影响,发现通过单向不可逆非线性能量泵实现非线性振动控制,优化系统参数,使冲击激励下不接地系统能量达到89%的耗散。Ma等人 [10] 利用有限元方法对斜裂纹悬臂梁的动力特性进行了分析。
以上文献大部分采用Galerkin方法研究悬臂梁结构的非线性动力学特性,而很少有学者用微分求积(DQ)法对悬臂梁的非线性动力学性质进行分析。Galerkin方法是基于变分原理将原问题转化为求泛函的极小值的一种近似方法。用Galerkin方法求解会遇到许多原则性的困难,主要有:1) 试函数的选取,也就是我们常说的取模态;2) Galerkin方程的形成需要大量的积分,当取的项较多时,非线性项的显式表达式很难求出。因此大部分非线性动力学问题用伽辽金方法分析时仅提取有限的低阶振型函数近似处理,因而具有一定的局限性。微分求积法是近几十年发展起来的一种求解偏微分方程的数值近似方法,其基本原理是由美国学者 [11] Bellman和Casti于1971年提出的,其实质是用求解域上全部节点的函数值进行加权求和来表示函数及其导数在给定节点处的值,因而可以将微分方程变为以节点处的函数值为未知数的代数方程组或常微分方程组。微分求积法是一种全局方法,相比于Galerkin方法原理简单(不依赖变分原理),计算量小,对非线性动力学方程可以直接求解,减少了Galerkin方法寻找模态函数的麻烦,克服了Galerkin方法处理问题时仅提取有限低阶振型的局限性,本质上考虑了所有振型的综合贡献。
1987年Bert首次 [12] 将微分求积法用于简单结构元件的力学分析,从此掀起了微分求积法在工程结构中应用的研究热潮。截至目前,微分求积法的发展和应用都是针对各种工程结构的静力、稳定性和自由振动分析 [13] - [19] ,而将微分求积法直接用于非线性偏微分动力学方程的求解进行复杂非线性动力学分析的文献还很少。本文将微分求积法推广到悬臂梁非线性偏微分动力学方程的求解,针对悬臂边界条件,提出一种新的微分求积施加边界条件方法,即将由微分求积法离散得到的边界代数方程连同内部的控制微分方程联合组成代数微分方程组求解,进而结合非线性动力学理论对受横向载荷和轴向载荷联合作用下的粘弹性悬臂梁的非线性动力学行为进行分析。
2. 粘弹性悬臂梁的控制方程
粘弹性悬臂梁的动力学模型如图1所示,粘弹性悬臂梁受到横向载荷
和轴向载荷
的联合作用。假设梁的长度为
,截面积为
,密度为
。
是粘弹系数,
是杨氏模量,
是截面惯性矩。假设轴向载荷
在常态
上有一小的扰动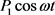 ,即
。
,即
。
根据Kelvin粘弹本构关系和哈密顿原理,建立粘弹性梁悬臂梁的横向振动控制方程如下:
(1)
边界条件
, (2a)
.(2b)
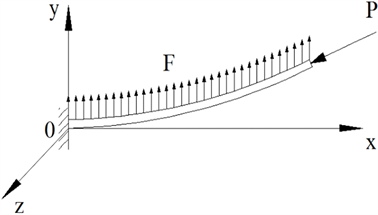
Figure 1. The model of viscoelastic cantilever beam
图1. 粘弹性悬臂梁模型
3. 微分求积法求解控制方程
微分求积法的基本原理是将函数在求解区域内的每个网格点处的导数值用域内全部网格点上的函数值的加权线性和近似表示。关于微分求积法的理论在文献 [20] 中有详细的论述,包括权系数的计算、节点的选取、边界条件的处理等。
3.1. 控制方程的离散
假设梁的长度 = 1 m,则方程(1)的求解区间为
。在区间
上取
个互异节点
。取
,节点坐标如下
. (3)
利用微分求积法则,方程中的未知函数在各节点处的各阶导数值表示如下
(4)
其中
分别是微分求积法中一阶导数、二阶导数、三阶导数、四阶导数的权系数,
表示函数
在各节点处对时间
的一阶导数。(4)式写成矩阵的形式如下
(5a)
(5b)
(5c)
(5d)
(5e)
(5f)
(5g)
3.2. 边界条件的处理
由于在端点
处,未知函数的一阶导数为0,即
,因此
的第一行为0。同理,在端点
处,未知函数的二阶导数为0,即
,因此
的最后一行为0。一阶导数和二阶导数的权系数矩阵分别修正 [20] 为
(6)
(7)
在计算三阶导数矩阵和四阶导数矩阵时,可以用矩阵乘积得到,即
,
(8)
这样就引入了这两个边界条件。又由于端点
处,函数值也为0,即
,因而不用求,只求内部节点及端点
处的函数值即可,因此权系数矩阵的第一行,最后一行,第一列及最后一列划掉。此时只剩边界条件
. (9)
内部节点及端点
处的各阶导数表达式用矩阵可以表示为
, (10a)
, (10b)
类似地
,
, (10c)
,
, (10d)
. (10e)
将(10)代入控制方程及边界方程得
(11)
.(12)
其中
表示两向量对应元素的乘积。(11)是一常微分方程组,含有
个方程,
个未知量
,要求解该方程,还需一个条件,而(12)是一代数方程,可以通过(12)得到
一个未知量的表达式 [20] ,代入方程(11),则方程(11)成为一完全的常微分方程组,进而可以求其解。
这个代入求解过程需要非常大的计算量且不利于编制程序。因为
,因此方程组(11)、(12)联合
组成指标 [21] 为1的微分代数方程组,可以应用隐式龙格库塔方法直接求解。因此本文针对悬臂边界条件中三阶导数为0,没有采取微分求积法中传统的处理边界条件方法,而是将边界条件用微分求积法则离散得到的代数方程连同内部控制常微分方程组联合组成微分代数方程组直接求解,这样就省去代入法求解的计算量且可以直接编制程序进行计算。
4. 数值结果
本文给定参数和初始条件
,
,
,
,
,
,
,应用隐式龙格库塔方法对微分代数方程组(11)、(12)进行
求解。在数值结果的基础上以梁中点处的位移代表梁横向振动的位移,分别作出了横向振动位移随横向载荷幅值及频率变化的分叉图、研究了二者对粘弹性悬臂梁横向振动的非线性动力学行为的影响。并作出了由分叉图得出的一些典型的相同参数下的周期运动和混沌运动的时间历程图、相图及庞加莱截面。
4.1. 横向载荷幅值的影响
图2是粘弹性悬臂梁横向振动位移随横向载荷幅值
在区间
上变化,横向载荷频率
时的分叉图。从图2可以看出当
在区间
上变化时,运动是周期的;由100 N变化到780 N时,系统运动是单倍周期的;随着
的增大,出现了一个小的2倍周期窗口;当
由820 N
增大直到最后,周期运动分叉为混沌运动了。
4.2. 横向载荷频率的影响
图3是粘弹性悬臂梁面内振动横向位移随横向载荷频率
在区间
上变化,横向载荷幅值
时的分叉图。从图3可以看出当频率
较小时,系统运动是单倍周期的,随着
的增大,大约在22 Hz时,运动由周期变为混沌。当频率
继续增大到40 Hz时,混沌运动消失,又出现单倍周期运动,而且单倍周期的窗口较大,直到
增大到72 Hz时,单倍周期运动分叉为混沌运动直到最后。在混沌窗口存在一些多倍周期运动。
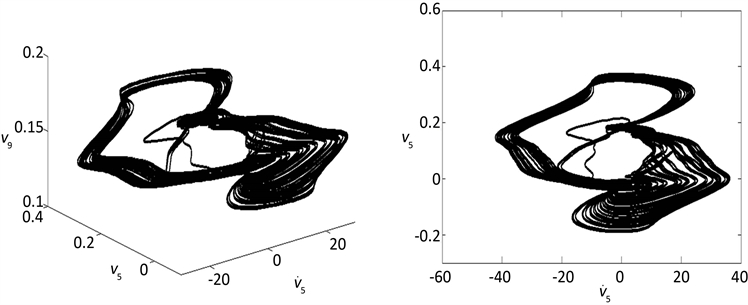
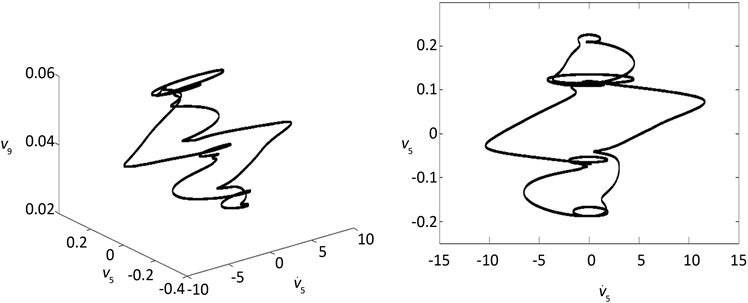
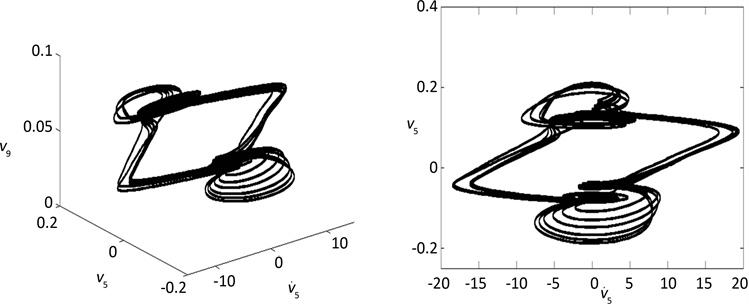
图4~图8是一些典型的周期运动和混沌运动的相图、时间历程图以及庞加莱截面。其中:a) 是以梁的速度,梁中心位移、以及梁另外一点位移为横、纵、竖坐标的三维相图,b) 是以梁的速度、梁中心位移为横纵坐标的二维相图,c) 是以梁的速度、梁中心位移为横纵坐标的庞加莱截面图,d) 是梁的横向振动位移随时间变化的时间波形图。从这些图形中可以看出,在相同参数下,无论是从相图,还是时间历程图所得的粘弹性悬臂梁横向非线性振动的动力学性质是相同的。
5. 结论
本文的创新之处1) 将微分求积法应用到悬臂梁结构的非线性动力学研究中,针对悬臂梁结构的边界条件,提出了一种微分求积处理边界条件的新方法,也就是将离散的常微分方程组和边界代数方程联合组成微分代数方程组,再利用隐式龙格库塔法进行求解;2) 利用微分求积法以及新的施加边界方法分析了受横向载荷和轴向载荷联合作用的粘弹性悬臂梁的非线性动力学行为。利用分叉图,研究了横向载荷
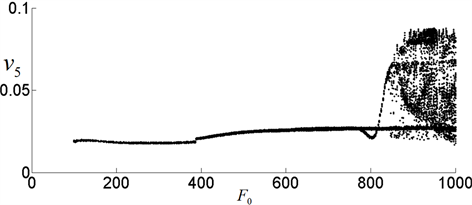
Figure 2. Effect of the amplitude of transverse load
图2. 横向载荷幅值的影响
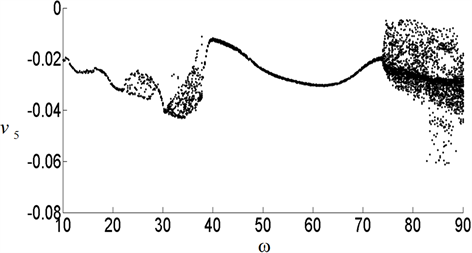
Figure 3. Effect of the frequency of transverse load
图3. 横向载荷频率值的影响
 (a) (b)
(a) (b)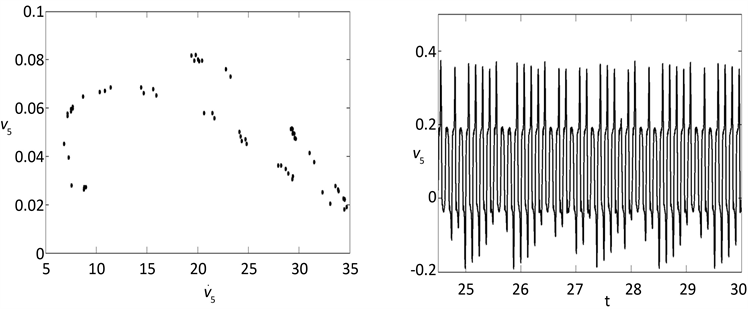 (c) (d)
(c) (d)
Figure 4. Chaotic motion appears when F = 1000 N, ω = 20 Hz
图4. F = 1000 N,ω = 20 Hz时粘弹性悬臂梁的混沌运动
 (a) (b)
(a) (b)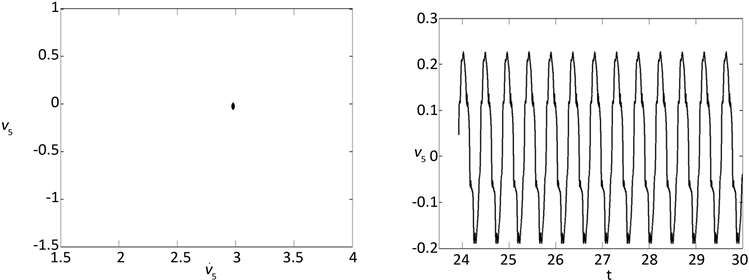 (c) (d)
(c) (d)
Figure 5. Periodic-1 motion appears when F0 = 500 N, ω = 13.6 Hz
图5. F0 = 500 N,ω = 13.6 Hz时粘弹性悬臂梁的1倍周期运动
 (a) (b)
(a) (b) (c) (d)
(c) (d)
Figure 6. Periodic-2 motion appears when F0 = 500 N, ω = 25 Hz
图6. F0 = 500 N,ω = 25 Hz时粘弹性悬臂梁的2倍周期运动
 (a) (b)
(a) (b)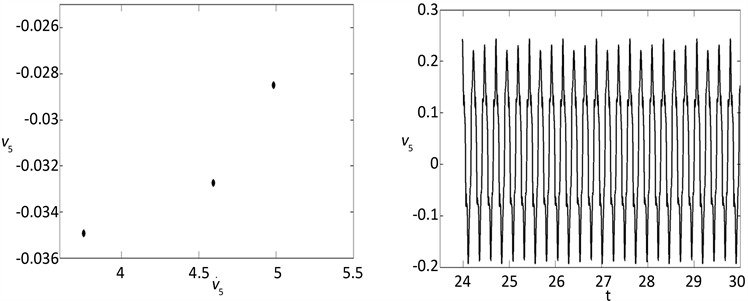 (c) (d)
(c) (d)
Figure 7. Periodic-3 motion appears when F0 = 500 N, ω = 26.2 Hz
图7. F0 = 500 N,ω = 26.2 Hz时粘弹性悬臂梁的3倍周期运动
 (a) (b)
(a) (b)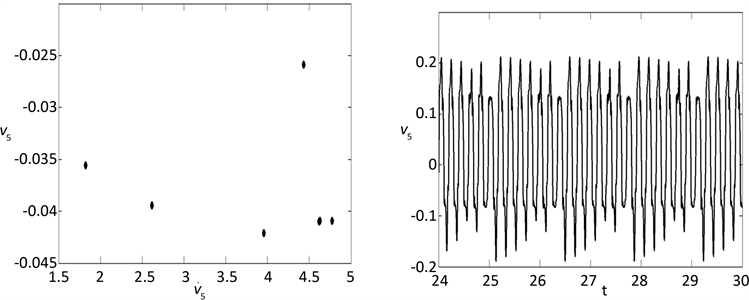 (c) (d)
(c) (d)
Figure 8. Periodic-6 motion appears when F0 = 500 N, ω = 32.4 Hz
图8. F0 = 500 N,ω = 32.4 Hz时粘弹性悬臂梁的6倍周期运动
幅值及频率对其非线性动力学性质的影响。为了验证由分叉图得出的结论,作出了一些周期和混沌运动的相图、庞加莱截面以及时间历程图,从这些图形得到的在相同参数下粘弹性悬臂梁的动力学性质是一致的。以上研究结果表明微分求积法以及新的边界条件施加方法可以用来分析悬臂梁结构的的非线性动力学性质,但是微分求积法及新的施加边界条件新方法的有效性还需要做进一步的研究,从理论上论证以及和其它近似方法结果相比较,将是我们下一步的工作。
基金项目
国家自然科学基金(11502165)。