1. 引言
能源是人类赖以生存的物质基础,也是推动人类社会进步的动力来源。但是,随着社会的发展,也给人类带来许多问题,其中,传统能源发电引起的环境污染问题更为显著 [1] 。由此,人们开始寻求新型清洁能源来代替传统能源。而太阳能的绿色环保优势逐渐引起人们的重视。2015年全球总装机容量超过50 GW,同比增长16.3%,累计装机容量超过230 GW [2] 。但目前来看,光伏发电效率还比较低,间歇性、波动性显著,对光伏系统来说,应当寻求光伏电池的最优工作状态,使得光伏出力达到最大限度,因此,研究一种稳定高效的最大功率跟踪方法显得尤为重要。
到目前为止,国内外专家研究出多种MPPT控制算法,比如电导增量法,扰动观测法等。而扰动观测法由于它的简单,是最常用的一种方法。扰动观测法的基本思想是通过扰动光伏电池的输出电压,达到输出功率的变化,根据功率变化的趋势改变扰动电压方向,使光伏电池最终工作于最大功率点 [3] 。而定步长的扰动观测法存在振荡和误判问题,使系统不能够准确地追踪到最大功率点,造成能量损失,因此需要变步长进行改进及优化。
最优梯度法是传统的一种变步长寻优方法。该方法根据P-U特性曲线,选取目标函数的正梯度方向作为每步迭代的搜索方向,逐步逼近函数的最大值。定义正梯度为
(1)
其中
。则梯度迭代法可写成
(2)
可见,基于最优梯度法的MPPT控制方法实际是按光伏电池P-U特性曲线的斜率而自动变化电压扰动的步长 [4] 。P-U特性曲线如图1所示。
由P-U特性曲线图可知,在功率最大值两侧的曲线斜率基本保持不变,因此,在初步跟踪时几乎是定步长跟踪,速率较低,并且在接近最大值时,电压波动范围较窄,若步长较大,很难在最大功率点处稳定。基于该种方法的不足,本文提出一种改进型变步长自适应扰动观测算法,并通过Simulink环境仿真,从最大功率的转换角度研究MPPT,与最优梯度法进行对比分析,验证了该方法的有效性和可靠性。
2. 光伏电池建模
光伏电池是由多个能产生光电流的二极管串并联组成, 随着光照的强度的增加而增加,但与温度成负相关关系。当外界光照,温度不变时,光伏电池可看作为恒流源,其等效电路图如图2所示。
图2中,Iph代表光子在光伏电池中的激发电流,Id为太阳能电池内部pn结的总扩散电流,Rs为串联电阻,Rsh为并联电阻,短路电流为Isc,开路电压为Uoc。需要明确指出的是Isc的大小取决于光照强度与环境温度的影响 [5] 。
在实际工程中,需要根据厂家提供的Isc、Uoc以及最大功率点时的Im和Um,因此在工程中常用的数学表达式为:
(3)
式中包含Isc和Uoc两个原始参数,而此时的问题是C1与C2的值。通过计算,令
(4)
将式(4)带入到式(3)中,得:
(5)
最后将式(5)带入式(4)中解出C2的值,从而得出光伏电池的工程数学模型表达式。
上述过程是按标况(照度Sref = 1000 W/m2,温度Tref = 25℃)下得出的。由于外界环境变化对光伏电池发电影响较大,所以,标况下的光伏电池数学模型已不再适用,需对其修改补偿得出一般工况下的光伏发电数学模型。

Figure 2. Photovoltaic cell equivalent model
图2. 光伏电池等效模型
设标况与一般工况的光照强度与温度差分别为
和
。则
(6)
(7)
根据式(6)和式(7)对一般工况的Isc、Uoc、Im以及Um进行补偿,得
(8)
(9)
(10)
(11)
其中,
,
,
。将补偿后的各个参量带入到式(4)和式(5),求出补偿后的
和
,根据式(3)~(11)得出一般标况下的光伏电池发电的数学模型 [6] 。在Simulink环境下搭建光伏电池物理模型,如图3所示。
3. 最大功率跟踪模型分析
根据戴维南定理与最大功率定理可知,负载阻抗与系统内部阻抗相匹配时,达到功率最大点。即:
(12)
然而,在实际工程应用当中,负载一旦确定,不易更改,但光伏板的功率曲线受外界环境影响较大,在负载不变的前提下,很难长时间在一个功率最大点运行,因此必须保证负载阻抗随着光伏板的变化而变化。在此利用升压电路原理,通过改变占空比的方法,达到阻抗变换以及匹配的目的。升压电路图如图4所示 [7] 。
由图可知,该电路由IGBT分成两部分,根据电能变换功率守恒原理,即:
(13)
根据升压电路原理,设占空比为
,则输出电压
与输入电压
关系为:
(14)
由式(13)和式(14)联立可得:
(15)
Figure 3. Photovoltaic cell physics model
图3. 光伏电池物理模型
根据欧姆定律可得输入阻抗
与输出阻抗
之间的关系。
(16)
由式(16)可得,在负载不变的情况下,随着外界环境的变化,光伏板电池内部阻抗在不断变化,通过改变占空比,能够使得输出阻抗不停地与输入阻抗匹配。可见,调节占空比可以实现光伏板电池的最大功率跟踪,且输出阻抗与占空比呈负相关。
4. 变步长自适应扰动法原理
根据最优梯度法的不足和P-U特性曲线单峰值的特点,不必考虑全局寻优的问题,只需比较前后时刻功率差
的符号即可,若为正,则
,继续向同方向扰动,反之,则向反方向扰动,由此实现最大功率跟踪的快速性 [8] 。
(17)
为占空比增量,a为步长因子系数。式(17)可得,采用前后时刻功率差值作为变步长的扰动步长因子,随着功率趋近最大值的程度,差值的模也会随之改变,从而实现自适应跟踪目。
考虑到P-U特性曲线的最大值只是一个点,设计功率跟踪的过程中,很难达到在一个点稳定,并且在寻优波动的过程中,会消耗一部分功率,因此,设定一定的阈值功率,随着不断地靠近目标点,前后时刻的功率差值也在不断地缩小。若波动在阈值范围内,则视为功率达到最大,扰动因子强制置零,系统占空比不再变化,完成最大功率跟踪。在外界条件不变的情况下,仍能保持系统运行在最大功率点 [9] 。由此减小了功率的波动程度,减少了功率损失,同时增加了系统的稳定性。
阈值的设计主要参考占空比的单位增量所引起的功率增量
与系统输出的精度,不能过小,但也不能太大。而
的变化大小取决于a与
的乘积,决定了系统的调节精度与速度。a越小,精度越高,但调节速度越低,反之则越高。所以还需要根据工程运行条件进行合理地设计,本文设定阈值为50 W。结合式(16),搭建MPPT控制器,如图5所示。
5. 仿真及数据分析
在Simulink环境下搭建完整的太阳能电池最大功率跟踪系统,分别从改进变步长法与最优梯度法两种方法进行仿真分析。设定环境温度为恒温25℃,光照强度由初始状态的800 W/m2到600 W/m2再到1000 W/m2变化,负载为10 Ω,运行时间1.5 s。从系统的
曲线变化,系统功率跟踪以及占空比三个方面分析改进型变步长自适应法和最优梯度法的系统性能。
5.1. 系统∆P曲线变化分析
曲线变化如图6所示。(a)图为改进后的功率波动图,(b)图为最优梯度法功率波动图。由于改进型方法设定了功率阈值,所以功率的波动被限制在50W以内。结合图(a)和图7中可以得出,随着光照强度的增加,系统功率在不断增加,但系统的
也在增大,但都没有超出阈值范围。
5.2. 系统功率跟踪分析
从图7可以看出,在相同的外界条件下,两种方法都可以对光伏电池的最大功率进行跟踪,但追踪过程的效果却相差很大,以下由追踪效率和获得的最大功率两方面进行分析。
5.2.1. 追踪速率方面
在外界光照强度变化的情况下,改进型有较为明显的优势,在0.06 s以内即可达到系统的最大功率点,而最优梯度法则在0.1 s左右。在实际应用中,外界环境时时刻刻都在变化,最大功率点也在不断改变,改进型的快速性对外界条件的变化有更好的适应性。
5.2.2. 最大功率方面
两种方法的最大功率跟踪过程图如图7所示。
改进型获得的最大功率高于10 KW,而最优梯度跟踪法停留在10 KW的点处波动,以此为系统功率的最高点。另外,在光照强度变化后,系统功率相继出现变化,达到稳定后,最优梯度法获得的最大功率也没有改进型高。由此得出在跟踪质量上改进变步长自适应法要优于最优梯度法。
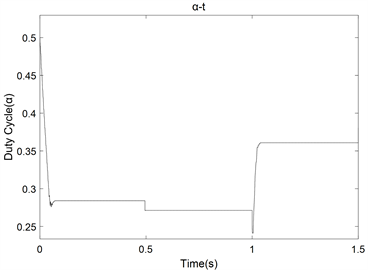
5.3. 占空比分析
由于系统的最大功率跟踪是通过升压电路获得,所以通过IGBT的占空比可观察到系统最大功率的跟踪过程。占空比变化曲线如图8所示。从图中可以得知,两种方法的占空比曲线走势基本一致,系统在获得最大功率点后,占空比能够保持不变,系统稳定。但从曲线中看可以看到最优梯度法波动时间较长,且在光照强度800 W/m2到700 W/m2变化过程中,(b)图没有明确显示出占空比的变化,说明其追踪精度及对光照变化的灵敏度不高。此外,从图中还可以看出光照强度在800 W/m2时,改进型变步长自适应方法占空比小于最优梯度法,结合式(16),再次证明了改进后的方法在功率跟踪的质量高于最有梯度法。
6. 结论
本文所设计的改进型变步长自适应扰动观察法保留了扰动观察法的思想,从功率转换的角度设计,应用电能变换技术,利用前后时刻的功率差值改变占空比,不停地改变扰动步长,从而起到对电压的扰动作用,实现阻抗自动匹配。除此之外,设定功率阈值,降低在最大功率点的波动程度,减少功率损耗,最终完成最大功率跟踪的目的。
通过在Simulink环境下搭建模型仿真以及对结果数据进行仿真,从最大功率跟踪的转换过程角度和功率最高点的扰动情况方面分析,并且与传统的最优梯度扰动观察法进行了对比研究,最终得出改进型变步长自适应扰动观察法无论在追踪速率上和追踪质量上都要优于最优梯度法的结论,并且对外界环境
 (a)
(a) 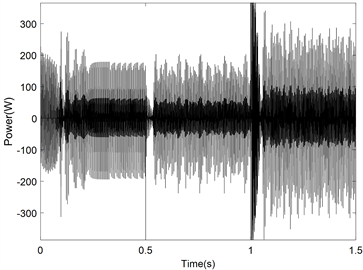 (b)
(b) (c)
(c)
Figure 6. Power fluctuation diagram. (a) Improved step-by-step adaptive method ΔP curve; (b) optimal gradient method ΔP curve; (c) set the threshold of the optimal gradient method ΔP curve
图6. 功率波动图。(a) 改进型变步长自适应法∆P曲线图;(b) 最优梯度法∆P曲线图;(c) 设定阈值的最优梯度法ΔP曲线图
 (a)
(a)  (b)
(b)
Figure 7. Power tracking process diagram. (a) Improved variable step adaptive tracking process diagram; (b) the best gradient method to track the process
图7. 功率跟踪过程图。(a) 改进型变步长自适应跟踪过程图;(b) 最优梯度法跟踪过程图
 (a)
(a) (b)
(b)
Figure 8. Duty Cycle Variation Graph. (a) Improved variable step size adaptive duty cycle curve; (b) optimum gradient method duty cycle curve
图8. 占空比变化曲线图。(a) 改进型变步长自适应占空比变化曲线图;(b) 最优梯度法占空比变化曲线图
变化较为灵敏,在光照波动情况下,占空比能够迅速作出响应,短时间内寻找到最优点后稳定运行,适应于恶劣环境,并且通过调整功率阈值,能够调节追踪精度,有较好的实际应用价值。此外,本文也验证了最优梯度法由于P-U特性曲线两侧斜率基本不变而导致追踪速度慢与最大功率点处波动严重的实质。
致谢
本文是在王延平教授和王智森教授的指导下完成的,在仿真过程中提出了很多宝贵的意见,才得以在短时间内完成光伏电池的研究,在此向他们表示衷心的感谢。