雷达海杂波K分布序列模型仿真ZMNL和SIRP方法比较分析

Comparison and Analysis of Radar Sea Clutter K Distribution Sequence Model Simulation Based on ZMNL and SIRP

摘要: K分布序列模型是比较逼近真实海杂波特性的仿真模型，在海杂波仿真中应用广泛。而ZMNL和SIRP是产生海杂波随机序列常见的两种方法。本文介绍了ZMNL和SIRP两种方法产生海杂波随机序列的流程，然后对两种方法产生数据与真实海杂波数据的逼近程度进行了仿真。经过比较分析，相对于ZMNL法，SIRP法产生的海杂波数据在幅度分布和频谱特性更接近于真实数据，在计算速度允许的情况下优先选择SIRP法。

Abstract: K-distribution sequence model is a simulation model that approximates the real sea clutter characteristics, and it is widely used in sea clutter simulation. ZMNL and SIRP are two common methods to generate random clutter of sea clutter. This paper describes two methods of ZMNL and SIRP to generate sea clutter random sequence, and then the approximation of the data generated by the two methods and the real sea clutter data is simulated. After comparative and analysis, sea clutter data generated by the SIRP is closer to the real data in amplitude distribution and spectral characteristics than data generated by ZMNL, and SIRP method should be preferred when computational speed allows.

1. 引言

雷达对海探测过程中，海杂波的存在严重影响了对海上目标探测，因此海杂波特性分析及仿真一直是雷达工程人员很关心的问题。海杂波由海面后向反射产生，杂波幅度随时间和空间随机起伏，可用Rayleigh、对数正态、韦布尔等分布模型仿真。根据高分辨率雷达在低视角的海杂波数据，K分布的复合形式可以更好地与实测海杂波数据相匹配 [1] 。海杂波数据序列可由概率密度函数和自相关函数随机数产生，目前存在两种常见的相关随机序列的产生方法，零记忆非线性变换法(ZMNL)和球不变随机过程法(SIRP)，本文将对两种方法的仿真效果进行比较和分析。

2. NL法模拟相关K分布海杂波

零记忆非线性变换法(ZMNL)的思路是 [2] ：采用非线性变换将高斯过程变换为具有伽马统计特性的过程，简单地把局部功率和散射分量相乘就可以生成K分布杂波。仿真相关伽马过程的方法是以一个零均值、单位方差的相关高斯过程作为出发点，随后通过解下面方程得到零记忆非线性变换将其映射到一个伽马过程 $y$ ：

$\frac{1}{\text{2π}}{\displaystyle {\int }_x^{\infty }\exp \left(\frac{-{x^{\prime }}^2}{2}\right)\text{d}{x}^{\prime }}=\frac{1}{\Gamma \left(v\right)}{\displaystyle {\int }_y^{\infty }{y^{\prime }}^{v-1}\exp \left(-y^{\prime }\right)\text{d}{y}^{\prime }}$ (1)

与产生高斯时间序列和具有指定相关性随机场的标准方法相结合，这种方法可以产生具有伽马单点统计特性的相关时间序列和随机场，在输入和输出过程的相关函数之间可以建立直接的联系。K分布杂波模型由基于幅度调制的基本分量并且服从伽马分布的照射空间变化引起的散射束电平变化分量，其中伽马分布具有长相关时间慢变化的特点；还有快变化的斑点分量，它是短时间相关并且服从瑞利分布。假设 $z^2$ 便是两个独立随机变量瑞利和伽马分布的乘积 [3] ：

$z^2=X\cdot Y$ (2)

$X$ 是符合瑞利分布的随机变量， $Y$ 是符合伽马分布的随机变量。

只需分别生成上述两个随机序列，然后利用 $z=\sqrt{X\cdot Y}$ 就可以产生所需要的K分布序列。按照ZMNL模型，可以由相关复高斯随机序列和一个非复实平稳随机序列相乘得到复K分布序列，产生方法如图1所示。

其中， ${\nu }_{1,i},\cdots ,{\nu }_{\theta -1,i}$ 为同分布、相互独立的高斯白噪声序列，服从 $N\left(0,{\sigma }^2\right)$ 分布； ${\nu }_{\theta ,i},\cdots ,{\nu }_{\theta +1,i}$ 为独立且不相关的高斯白噪声序列，服从 $N\left(0,1\right)$ 分布。

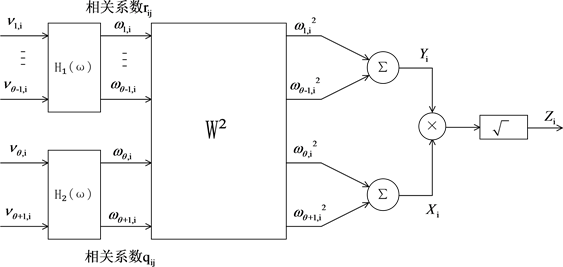
Figure 1. Principle diagram of K-Distribute clutter by ZMNL

图1. ZMNL法相关K分布杂波产生原理图

两组序列分别通过各自设计的滤波器后，产生的 ${\omega }_{1,i},\cdots ,{\omega }_{\theta -1,i}$ 序列之间全部不相关，再经过一系列变化后产生的前 $\theta -1$ 个变量的和生成调制分量，其中 $Y_i$ 的相关系数为 $r_{ij}$ ；第 $\theta$ 和 $\theta +1$ 这两个分量经一系列变化后求和产生调制分量 $X_i$ ，其中 $X_i$ 的相关系数为 $q_{ij}$ 。K分布的随机序列则是由 $X_i$ 与 $Y_i$ 相乘后开平方后获得的。所以主要问题就是如何设计两个滤波器来产生瑞利和伽马分布。假设K分布的相关系数为 $S_{ij}$ 。那么则有

$S_{ij}=\frac{{\Lambda }^2\left[{}_{2}F{}_1\left(-1/2,-1/2;\nu +1,r_{ij}^2\right)\cdot {}_{2}F{}_1\left(-1/2,-1/2;1,q_{ij}^2\right)-1\right]}{\nu +1-{\Lambda }^2}$ (3)

$\Lambda =\frac{\Gamma \left(\nu +3/2\right)\Gamma \left(3/2\right)}{\Gamma \left(\nu +1\right)}$ (4)

${}_{2}F{}_1\left(\alpha ,\beta ;\gamma ,z\right)=\frac{\Gamma \left(\gamma \right)}{\Gamma \left(\alpha \right)\Gamma \left(\beta \right)}{\displaystyle \underset{n=0}{\overset{\infty }{\sum }}\frac{\Gamma \left(\alpha +n\right)\Gamma \left(\beta +n\right)}{\Gamma \left(\gamma +n\right)}}\frac{z^n}{n!}$ (5)

其中， ${}_{2}F{}_1\left(\alpha ,\beta ;\gamma ,z\right)$ 是高斯超几何分布函数， $\nu$ 是形状参数。

确定 $S_{ij}$ 的值并不能确定 $r_{ij}$ 和 $q_{ij}$ 的值，根据给给定不同的形状参数值 $\nu$ 来确定两组数列的相关系数 $r_{ij}$ 和 $q_{ij}$ 。

3. IRP法模拟相干相关K分布海杂波

与ZMNL方法不同，SIRP方法先随机产生一组相关的高斯序列，然后按照特定的概率密度函数对产生的高斯序列进行调制。SIRP方法的优点在于能够生成复相关杂波序列，但是序列阶数和自相关函数过大时，会导致计算量快速增加，计算速度变慢。K分布基于SIRP方法的模拟过程如图2所示 [4] 。

图2中，m是一个复高斯白噪声序列，n是实高斯白噪声序列。线性滤波器 $H_1\left(\omega \right)$ 由最终输出K分布序列z的相关系数设计决定，使得序列y和z具有相同的相关系数。线性滤波器 $H_2\left(\omega \right)$ 往往是一带宽很窄的低通滤波器从而使随机序列的功率谱足够窄，使得生成的高斯序列x具有高度的相关性。ZMNL变换使得输出的x的PDF为杂波的特征PDF。x服从广义 $\chi$ 分布，即

$f_{\chi }\left(x\right)=\frac{2{\nu }^{\nu }{x}^{2\nu -1}}{\Gamma \left(\nu \right)}\exp \left(-\nu x^2\right),x\ge 0$ (6)

Figure 2. Principle diagram of correlated K-Distribute clutter by SIRP

图2. SIRP法相干相关K分布杂波SIRP方法原理图

$H_1\left(\omega \right)$ 用傅里叶级数展开法来计算生成，将网络频率特性展开成傅里叶级数的方法求滤波器加权系数。非递归滤波器的差分方程如下：

$y_n={\displaystyle \underset{i=0}{\overset{N}{\sum }}{a}_i}{x}_{n-i},0\le n\le N$ (7)

其中， $x_{n-i}$ 是滤波器第 $n-i$ 个输入， $y_n$ 是滤波器的第 $n$ 个输出， $a_i$ 是滤波器加权系数。

通过Z变换求出的滤波器传递函数是：

$H\left(z\right)={\displaystyle \underset{i=0}{\overset{N}{\sum }}{a}_i{z}^{-i}}$ (8)

SIRP法产生K分布模型，首先要生成广义 $\chi$ 分布随机序列 $s\left(k\right)$ ， $s\left(k\right)$ 的平方就是所需要的伽马分布序列，对于SIRP非线性变换为：

$\frac{\gamma \left(\nu ,s^2\right)}{\Gamma \left(v\right)}\mu \left(s\right)=1-Q\left(z\right)$ (9)

其中， $\gamma \left(q,p\right)$ 是不完全欧拉函数。

也可以表示成：

$g\left[v,E\left(y^2\right)s^2/\left({\alpha }^2\text{π}\right)\right]=1-Q\left(z\right)$ (10)

其中， $g\left(a,b\right)=\frac{1}{\Gamma \left(b\right)}{\displaystyle {\int }_0^a{\text{e}}^{-t}}{t}^{b-1}\text{d}t$ 是不完全的伽马函数， $y$ 是滤波器 $H_1\left(\omega \right)$ 的输出， $v$ 是形状参数， $\alpha$ 是尺度参数。

又因为 ${\alpha }^2=\frac{{\sigma }^2}{2\nu }$ 并且 $E\left(y^2\right)={\sigma }^2$ ，所以式(10)变换成

$g\left(v,2v{s}^2/\text{π}\right)=1-Q\left(z\right)$ (11)

$Q\left(z\right)={\displaystyle {\int }_x^{\infty }\frac{1}{\sqrt{2\text{π}}}\exp \left(-\frac{u^2}{2}\right)\text{d}u}$ (12)

$Q\left(z\right)$ 是标准正态的尾部面积，式(11)可进一步表示为下式。

$g\left(v,2v{s}^2/\text{π}\right)=\frac{1}{2}+\frac{1}{2}erf\left(\frac{z}{\sqrt{2}}\right)$ (13)

其中 $erf\left(x\right)$ 是误差函数，其表达式为式(14)。

$erf\left(x\right)=\frac{2}{\sqrt{\text{π}}}{\displaystyle {\int }_0^x\exp \left(-u^2\right)\text{d}u}$ (14)

采取二分法求解式(13)线性方程，然后就可以求出序列 $s\left(k\right)$ 。

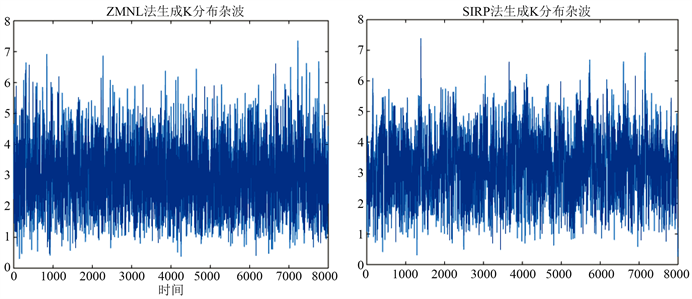
Figure 3. K-Distribute random sequence by ZMNL and SIRP

图3. ZMNL法和SIRP法生成K分布随机序列

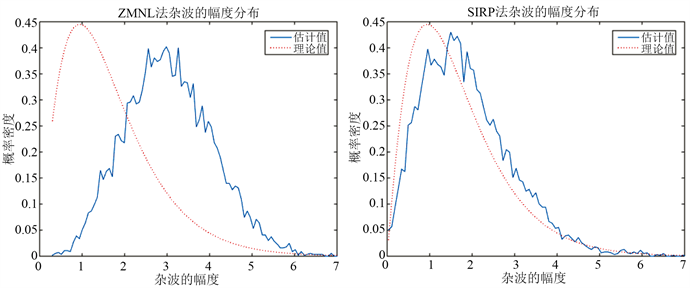
Figure 4. K-Distribute probability intensity function generated by ZMNL and SIRP

图4. ZMNL法和SIRP法生成K分布概率密度函数

Figure 5. K-Distribute clutter frequency spectrum by ZMNL and SIRP

图5. ZMNL法和SIRP法生成K分布杂波频谱

4. 布海杂波序列仿真结果及分析

通过ZMNL和SIRP法产生的K分布随机序列如图3所示。

由于海杂波幅度的随机性，上图中很难看出两种仿真方法产生的随机序列哪一个比较拟合K分布序列，对图3中的两组仿真序列进行了杂波幅度分布仿真如图4。

由杂波幅度分布图中我们能够清晰的看到，采用SIRP方法仿真的K分布海杂波序列要比采用ZMNL方法仿真的K分布海杂波更接近理想的海杂波序列。ZMNL方法产生的K分布序列也有较长的拖尾，但较SIRP方法生成的K分布序列还是不够明显。

对两组序列进行杂波谱分析的结果如图5所示，从图5中可以看出SIRP方法产生序列的杂波谱几乎与理论状态下的杂波谱拟合，但是ZMNL方法产生序列的杂波谱前面一段拟合还是较好，但当频率增高时，功率谱密度突然有了起伏，但大体上还是与理想状态下的杂波谱拟合，所以在传统方法仿真K分布序列时，采用SIRP方法比ZMNL方法能够更好地仿真海杂波序列。