1. 引言
海森堡测不准原理是量子力学的一个重要基本原理,它指出在一个量子力学系统中,一个粒子的位置和它的动量不可被同时确定。位置的不确定性
和动量的不确定性
一定满足不等式
,其中
是约化普朗克常数。类似的不确定性也存在于能量和时间、角动量和角度等许多物理量之间。因此在Fock空间及其推广的a-Fock空间上研究测不准原理是有意义的。早在文献 [1] 和文献 [2] 中作者就给出了Hilbert空间上的几种测不准原理形式,本文主要是将文献 [3] 的结果进行推广和完善。更多关于测不准原理的结果,感兴趣的读者可以查阅文献 [4] - [11] 。值得一提的是,由于参数
的引入,本文的计算结果相对文献 [3] 更为复杂,且当
时包含 [3] 中的所有结果。
下面对本文所用到的符号加以说明:
记
为一维复平面,
为一维实平面,对任意的正实参数
,我们定义:
为
上的Gaussian测度,其中
为
上的Lebesgue面积测度。
定义a-Fock空间
为:
其中
为
上整函数全体。显然
是
的闭子空间,因此
是Hilbert空间,其上的內积和范数分别定义为:
(1.1)
(1.2)
注:本文的所有结果都是在复平面
上讨论的,下文不再作说明。
2. 相关引理及主要结果
文献 [1] 中给出了一个泛函分析里的关于Hilbert空间
上的两个自伴算子测不准原理的一般性结果:
定理1:设
和
为Hilbert空间
上的可能无界的自伴算子,则对于任意的
和任意
有
(2.1)
其中
为
和
的换位子。等式成立当且仅当
和
相差一个纯虚数倍。
证明:详见 [1] 第27页。
在文献 [3] 中,陈泳和朱克和两位教授将定理1与海森堡测不准原理结合起来,得到了Fock空间
中的两个自伴算子的测不准原理。
定理2:令
,则对所有
有
等式成立当且仅当存在正实数
和复数
使得
证明:详见 [3] 中定理4的证明。
定理2中主要讨论了空间
上的由甄灭算子和产生算子构造的两个自伴算子,而这在
上不再适用,因为在
中,甄灭算子的对偶算子不再是产生算子了,稍作改变,我们得到:
引理1:对任意的
,令
为微分算子的常数倍,即
。则其对偶算子
为
。
证明:设
中的标准正交基为
可设
中稠密的两个多项式分别为
则
另外
于是
证毕。
从定理1我们知道,如果有两个自伴算子
和
使得
为恒等算子的常数倍,则可得到测不准原理。故我们考虑利用引理1中的算子
和
来构造这样两个自伴算子。
直接计算可知,对所有
有:
因此我们考虑
上的如下两个自伴算子:
即
(2.2)
由 [1] 知,若
,则
和
的定义都是合理的,若
和
都属于
,则
和
显然也都在
中,于是
和
的定义域的交集包含那些使得
(或
)仍旧在
中的
。对
,
及他们定义域的交,同样确定为算子
和
的定义域的交集。
引理2:对任意的
,对上述定义的自伴算子
和
,有
,其中
为
上的恒等算子,
为虚数单位。
证明:对所有
,由(2.2)式可得
证毕。
下面将给出a-Fock空间
上的第一个测不准原理形式。
定理3:对任意的
,令
,则对所有
有
(2.3)
等式成立当且仅当存在正实数
和复数
使得
证明:因为
,则由定理1可知
又因为
结合引理2可得
另外,由定理1可知(2.3)中等式成立当且仅当存在正实数
使得
(2.4)
或
(2.5)
这里,我们先计算(2.4)式有:
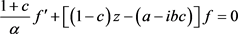 (2.6)
(2.6)
1) 若 ,则(2.6)只有解
,则(2.6)只有解 这一零解。
这一零解。
2) 若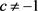 ,(2.6)式可变形为
,(2.6)式可变形为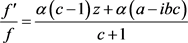 ,则由解常微分方程的初等方法可得(2.6)的一般解为
,则由解常微分方程的初等方法可得(2.6)的一般解为
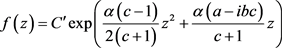 (2.7)
(2.7)
其中 为任意复常数。
为任意复常数。
由 [1] (第38页)知每个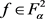 则必满足
则必满足
 (2.8)
(2.8)
因此函数(2.7)在空间 中的一个充要条件是
中的一个充要条件是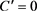 或
或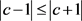 。由于
。由于 是实数,后者等价于
是实数,后者等价于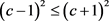 或
或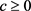 。而当
。而当 时,此时函数(2.7)为
时,此时函数(2.7)为
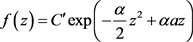
取 ,其中
,其中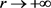 ,由(2.8)式知其等价于
,由(2.8)式知其等价于 。
。
对(2.5)式,同理可以讨论,证毕。
为了给出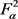 上的测不准原理的其他形式,我们还需对函数(2.7)进行一些相关的计算。
上的测不准原理的其他形式,我们还需对函数(2.7)进行一些相关的计算。
由定理3我们知道函数(2.7)在空间 中的充要条件为
中的充要条件为 或
或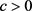 ,当
,当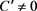 即
即 时,我们可以对函数(2.7)进行一些相关的计算,如范数、內积等,这些计算结果都将在下文推论中用到。由于
时,我们可以对函数(2.7)进行一些相关的计算,如范数、內积等,这些计算结果都将在下文推论中用到。由于 ,为了计算的简便,我们可将函数(2.7)的系数
,为了计算的简便,我们可将函数(2.7)的系数 去掉,得到下面一个与函数(2.7)相差复常数倍但形式更简单的函数。即
去掉,得到下面一个与函数(2.7)相差复常数倍但形式更简单的函数。即
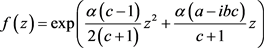 (2.9)
(2.9)
显然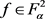 ,其中
,其中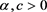 ,
, 。最后,我们只需将函数(2.9)的相应计算结果代入系数
。最后,我们只需将函数(2.9)的相应计算结果代入系数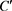 即可。
即可。
为了方便书写,我们将函数(2.9)简记为
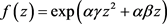 (2.10)
(2.10)
其中
 (2.11)
(2.11)
由于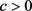 ,则
,则 。
。
我们令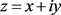 ,其中
,其中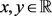 。给出相应计算如下:
。给出相应计算如下:
1) 对函数(2.9)计算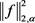 如下:
如下:
由(1.2)、(2.10)式得:
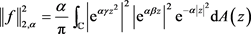 (2.12)
(2.12)
因为

则进一步计算(2.12)得:

其中
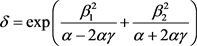 (2.13)
(2.13)
因为
 (2.14)
(2.14)
则
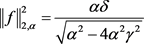 (2.15)
(2.15)
最后联立(2.11)、(2.13)和(2.15)式得:
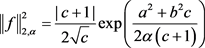 (2.16)
(2.16)
2) 对函数(2.9)直接计算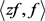 如下:
如下:
由(1.1)式和(1)的计算过程可得:
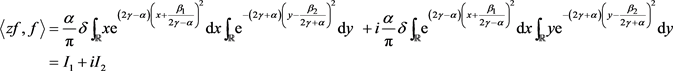
先计算 得:
得:

因为

于是
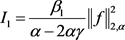 (2.17)
(2.17)
同理
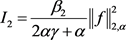 (2.18)
(2.18)
最后联立(2.11)、(2.17)和(2.18)式有
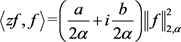 (2.19)
(2.19)
3) 对函数(2.9)直接计算 如下:
如下:
由(1.2)式和(2)的计算过程可得:

先计算 得:
得:
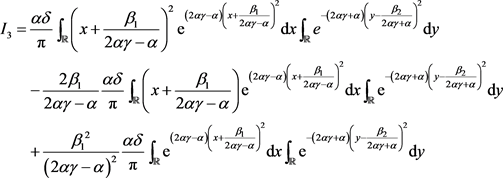
因为

进一步计算 得:
得:
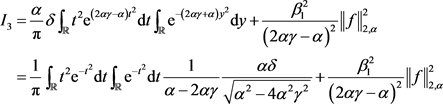
因为
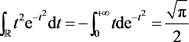
综上
 (2.20)
(2.20)
同理
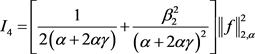 (2.21)
(2.21)
联立(2.11)、(2.20)和(2.21)式得:
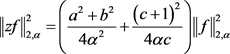 (2.22)
(2.22)
4) 对函数(2.9)直接计算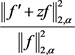 和
和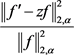 如下:
如下:
因为

同理

由(2.11)、(2.19)和(2.22)得
 (2.23)
(2.23)
同理
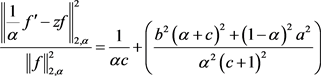 (2.24)
(2.24)
5) 对函数(2.9)直接计算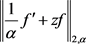 和
和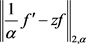 如下:
如下:
由(2.23)和(2.24)直接计算可得:
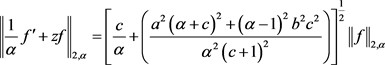 (2.25)
(2.25)
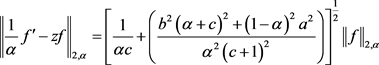 (2.26)
(2.26)
6) 对函数(2.9)直接计算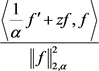 和
和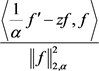 如下:
如下:
因为

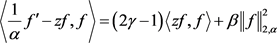
所以由(2.16)、(2.19)式有:
 (2.27)
(2.27)
同理
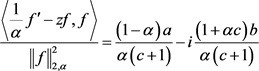 (2.28)
(2.28)
直接计算可验证,当 时,以上所有结果就是
时,以上所有结果就是 中相应的结果。
中相应的结果。
7) 最后给出最小值讨论。
对任意的 ,固定
,固定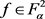 ,
, 为自伴算子,则对任意
为自伴算子,则对任意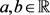 ,有
,有
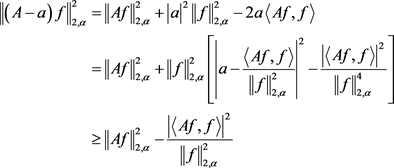
即可得
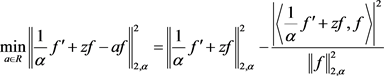 (2.29)
(2.29)
其中等号成立当且仅当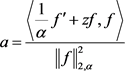 。
。
同理
 (2.30)
(2.30)
且最小值当 时取得。
时取得。
若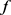 为
为 中的单位向量,即
中的单位向量,即 时,可得到如下测不准原理的第一个推论:
时,可得到如下测不准原理的第一个推论:
推论1对任意的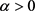 ,令
,令 为
为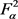 中的单位向量,则对所有
中的单位向量,则对所有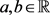 有
有

等式成立当且仅当
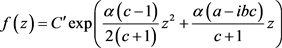 (2.31)
(2.31)
其中 为正实数,
为正实数,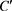 为复数且
为复数且
 (2.32)
(2.32)
证明:由(2.16)式可得函数(2.31)的范数为:

因为 ,直接计算得:
,直接计算得:

又因为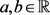 ,
,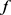 为
为 中的单位向量,则由定理3得:
中的单位向量,则由定理3得:
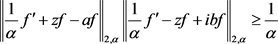
结合(2.29)和(2.30)对最小值的讨论得:
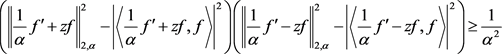
下面给出等号成立情形的详细证明:
1) 若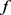 不具有(2.31)的形式,则由定理3可知对任意
不具有(2.31)的形式,则由定理3可知对任意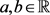 有
有

特别的我们令:

则由最小值讨论可得:

此时等号不成立。
2) 若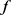 具有(2.31)的形式,为区别开来我们记为
具有(2.31)的形式,为区别开来我们记为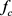 ,则由定理3可知
,则由定理3可知
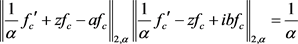 (2.33)
(2.33)
利用(2.27)和(2.28)直接计算内积可以得到

即当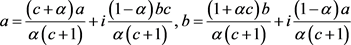 时,结合(2.29)、(2.30)式关于最小值问题的讨论可得
时,结合(2.29)、(2.30)式关于最小值问题的讨论可得

即不等式等号成立,证毕。
推论2:若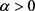 ,则对任意
,则对任意 有
有
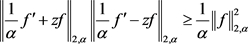
等号成立当且仅当存在正实数 和复数
和复数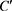 使得
使得
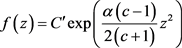 (2.34)
(2.34)
证明:在定理3中令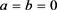 即可,证毕。
即可,证毕。
推论3:若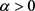 ,对任意
,对任意 有
有

其中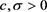 ,且
,且 。等号成立当且仅当存在正实数
。等号成立当且仅当存在正实数 和复数
和复数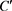 使得
使得
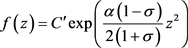
证明:由推论2可得
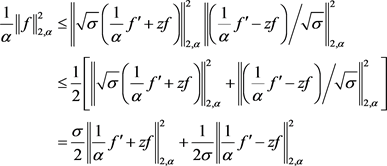
等号成立当且仅当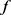 为形如(2.34)且
为形如(2.34)且

由(2.25)、(2.26)式及 知此等价于
知此等价于

证毕。
除了以上几种测不准原理的推论形式外,我们还可以给出一些关于角和距离的几何形式的测不准原理如下:
推论4:对任意的 ,令
,令 为
为 中任何非零函数,
中任何非零函数,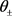 分别为
分别为 和
和 之间的夹角,则对所有
之间的夹角,则对所有 有
有

等式成立当且仅当

其中 为正实数,
为正实数,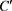 为任意非零复数。
为任意非零复数。
证明:由于

即
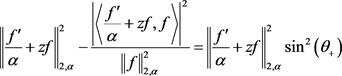 (2.35)
(2.35)
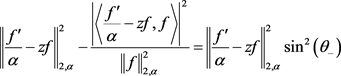 (2.36)
(2.36)
则由推论1知结论成立,证毕。
联立(2.35)、(2.36)、(2.23)、(2.24)、(2.27)、(2.28)式可分别计算得:
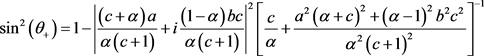

由此可求出此时两夹角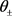 的大小。
的大小。
推论5:对任意的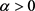 ,令
,令 为
为 中单位向量,则对任意
中单位向量,则对任意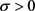 有
有
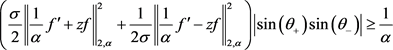
等号成立当且仅当 形如(2.31)且
形如(2.31)且 。
。
证明:由推论4得

再由推论3的证明方法有

等号成立当且仅当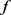 为形如(2.31)的函数且
为形如(2.31)的函数且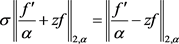
由(2.25)、(2.26)式知此等价于
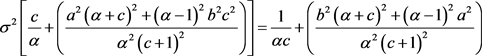
证毕。
推论6:对任意的 ,令
,令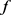 为
为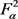 中单位向量,则
中单位向量,则
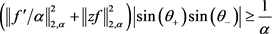
等成立当且仅当 形如(2.31)且
形如(2.31)且

证明:由推论5中取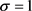 即得结论。证毕。
即得结论。证毕。
推论7:对任意的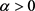 ,令
,令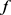 为
为 中的非零向量,则对所有
中的非零向量,则对所有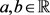 有
有
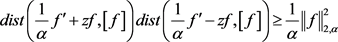
其中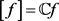 为
为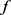 张成的一维子空间,
张成的一维子空间,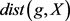 为
为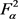 中
中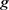 到
到 的距离。等式成立当且仅当
的距离。等式成立当且仅当
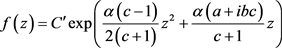
其中 为正实数,
为正实数,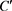 为非零复数。
为非零复数。
证明:因为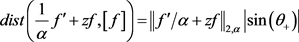 。
。
同理 ,则结论由推论4直接可得,证毕。
,则结论由推论4直接可得,证毕。
注:上述结论中的函数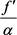 或
或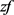 并不一定都属于
并不一定都属于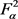 ,当
,当 或
或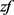 不属于
不属于 中时,上面所有结论中的每个不等式右边均为无穷大,综上,不等式总是成立的。
中时,上面所有结论中的每个不等式右边均为无穷大,综上,不等式总是成立的。
3. 复参变量下的测不准原理及其推广
注意到上面所讨论的测不准原理中 和
和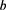 均为实参量,下面对
均为实参量,下面对 和
和 为复参量的情形做一个简单的讨论:
为复参量的情形做一个简单的讨论:
定理4:对任意的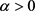 ,令
,令 ,则对所有
,则对所有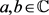 有
有
 (3.1)
(3.1)
等式成立当且仅当 和
和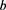 为实数且存在正实数
为实数且存在正实数 和复数
和复数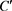 使得
使得

证明:记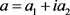 ,其中
,其中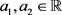 ,则
,则

同理记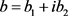 ,其中
,其中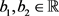 ,则
,则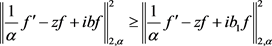 ,于是由定理3可知本定理成立,证毕。
,于是由定理3可知本定理成立,证毕。
以上所有结果均是对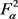 中的两个特殊的自伴算子
中的两个特殊的自伴算子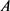 和
和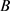 讨论的,事实上,将自伴算子
讨论的,事实上,将自伴算子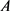 和
和 一般化,以上结论均可成立。
一般化,以上结论均可成立。
定理5:对任意的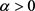 ,设
,设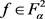 ,
, 为
为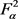 上的算子且满足
上的算子且满足 ,其中
,其中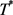 是
是 的对偶算子,
的对偶算子, 是任意正实参数。则对所有
是任意正实参数。则对所有 和
和 ,有
,有
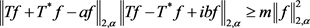
等号成立当且仅当 和
和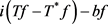 相差纯虚数倍。
相差纯虚数倍。
证明:同定理3的证法一致,证毕。
定理6:对任意的 ,设
,设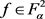 且
且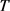 为
为 上的算子且满足
上的算子且满足 ,其中
,其中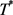 是
是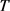 的对偶算子,
的对偶算子,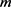 是任意正实参数。则对所有
是任意正实参数。则对所有 和
和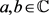 ,有
,有
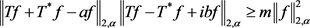
等号成立当且仅当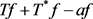 和
和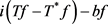 相差纯虚数倍。
相差纯虚数倍。
证明:同定理4的证法一致,证毕。
NOTES
*通讯作者。