1. 引言
在侧信道攻击中,针对于掩码实现的加密算法,其能量分析攻击在实现上一直是国内外硬件安全研究中的难点与重点。当加掩实现被证实不存在1阶泄漏之后,1998年,Kocher等人首先提出了针对于加掩实现的高阶攻击算法并定义了高阶DPA的概念,该方法的核心思想在于结合单条能量轨迹多个样本点 [1] 。2000年,Messerges从各方面完善了n阶DPA的定义,并系统介绍了2阶DPA的攻击方法,以加掩DES实现为范例对该方法进行了验证 [2] 。之后,以这些内容为基础,更多实用的方案和优化被提出。2006年,Oswald等人对2阶DPA的攻击方法进行了改进,并首次结合了模板攻击的方式,提出了基于模板的DPA攻击 [3] [4] 。但是,DPA作为无训练的攻击方式,在其算法存在的时间复杂度高,内存占用大,实际可用性难保证等问题上始终不能够得到实质性的解决。相对应的,模板攻击作为有训练的攻击方式,能够在一定程度上达到高阶DPA攻击所不能取得的效果。为此,我们采用高阶模板攻击的方式,提出了新的针对于掩码实施的攻击方式。
训练的概念,来自于数据分析中的有监督学习,属于数据分类问题中的一种类型,其所对应的是无监督学习。有监督学习指的是利用一组已知类别的样本,来调整分类器的参数,使其能够达到所要求的性能。该过程被称之为训练。经过训练后的分类器,可用于其它未知类别的样本,对其进行分类。模板攻击在统计学中属于分类算法,其攻击过程包括了对分类器参数的训练过程,即为有训练的攻击方式。而DPA攻击中不存在分类器,因此不需要对分类器参数进行训练,即为无训练的攻击方式。
本文的主要贡献在于,针对高阶DPA攻击中时间复杂度,效率,以及可行性方面存在的问题,对攻击方式进行了改进。并且,以新的思路提出了高阶模板攻击的算法,使得针对于掩码对策进行的能量分析攻击难题有了另一种解决方案。
文章结构如下:第1章对模板攻击原理及过程进行概述;第2章简要介绍加掩实现的思想和实现方式;第3章中分析高阶DPA攻击方式中存在的问题并尝试使用高阶模板攻击的方式对其进行改善;第4章以加掩AES实现为范例,使用高阶模板攻击的方式进行攻击测试,并分析实验结果;第5章全文总结并对今后研究进行展望。
2. 模板攻击
模板攻击利用了这样一个事实:能量消耗依赖于设备正在处理的数据。模板攻击使用多元正态分布对能量迹的特征进行刻画。与其他的能量分析攻击不同,模板攻击通常由两个阶段构成。第一个阶段对能量消耗特征进行刻画,第二阶段利用该特征实施攻击。即,模板攻击是一种有训练的攻击方式。
在模板攻击中假设,能量迹可以使用多元正态分布刻画,该多元正态分布由均值向量和协方差矩阵(m, C)来定义,并将(m, C)称为模板。
在模板攻击中,假设攻击者可以对被攻击设备的特征进行刻画,这意味着攻击者可以确定出某些指令序列的模板。攻击方式则是利用特征和从被攻击设备中获得的能量迹来确定密钥。将能量迹带入多元正态分布的概率密度函数中计算概率,概率值的大小反应了给定能量迹与模板的匹配程度。
直觉上,正确模板应该与最高概率相对应。因为每一个模板对应于一个密钥,故也可以由此给出关于正确密钥的信息。
模板攻击的本质是分类算法,其中的模板即为分类器。根据输入的能耗数据,使用模板将能迹识别为加密计算过程中的某个中间值(如轮密钥、S盒输出的汉明重量,高阶攻击中的掩码等)。在标准的模板攻击中,使用的是高斯识别算法作为分类算法。
3. 掩码对策
掩码技术的核心思想是使密码设备的功耗不依赖于设备所执行的密码算法的中间值。掩码技术通过随机化密码设备所处理的中间值来实现这个目标。掩码方案可以用下式来表示:
。
其中
表示密码运算过程中的中间值,m为掩码,通常是一个内部产生的随机数,
是经过掩码的掩码中间值,运算*通常根据密码算法所使用的操作进行定义,一般为布尔“异或”运算、模加运算或者模乘运算。在模加运算和模乘运算的情况下,模数根据密码算法进行选择。
在使用到掩码技术的加密过程(称之为加掩实现)中,可通过实验证明无法通过1阶DPA攻击得到正确的密钥。即,该实现不存在1阶泄漏。在次情况下,需使用到高阶能量分析攻击(高阶攻击在无说明的情况下特指2阶攻击)。
4. 高阶攻击
高阶攻击利用了掩码实现中的某种联合泄漏(2阶泄漏),该泄漏基于出现在加密过程中多个位置的中间值,如图1所示。出于性能,成本,及可行性等方面的考虑,掩码技术的典型实现是将同一个掩码应用于多个中间值之上。但是,即使在加密算法中使用多个掩码,这些掩码均在算法开始钱就已经生成完毕,之后才被应用于数据和密钥,并被算法操作所改变。因此,在一个高效实现中,总会发生如下的情况:一个掩码及相应的掩码型中间值均会出现在加密设备中。因此,研究利用两个中间值相关的联合泄漏的高阶DPA攻击就足够了,这类攻击被称为2阶DPA攻击。这两个中间值既可以是同一个掩码所对应的两个掩码型中间值,也可以是掩码型中间值及相应的掩码。
4.1. 二阶DPA攻击
高阶CPA攻击原理是,多个中间值的某种组合值与多个位置上能耗的某种组合值的相关系数不等于0。而具体的中间值组合方式则需要通过理论分析建模以及多次实验尝试来确定,待定目标则是能量泄漏模型及中间值联合泄漏位置。
实验中采用AES算法的加密能迹。我们选择
作为训练的目标中间组合值。其中,x为目标中间值,k为轮密钥。理论上该组合值与S盒输入输出能耗的乘积的相关系数为
,该值约等于0.06。其中,相关系数
的计算公式为:
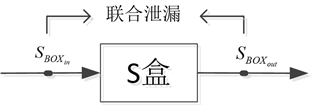
Figure 1. Joint leakage in energy trace diagram
图1. 能量迹中联合泄漏示意图
,
函数E为样本期望,函数D为样本方差。但由于实际的能耗中存在较强的噪音,该相关系数的实际值还会更小。且乘积运算易扩大能量迹中静态分量的差距,因此有必要使用到中心化来对能量迹进行预处理。
基于上述理论,一种较为简易的2阶DPA攻击的算法如下:
1) 假设一个P1与P2之间的间距,记为w,此时选择一个P1的起始位置A0,即可计算出相关系数P。
2) 不断向右移动P1的位置A,并将相关系数P记录下来。如图2所示。
3) 找到P的最大值,并将w减小,返回步骤1重复执行上述步骤。
4) 所有遍历结束后,挑选其中最大的相关系数P作为最终结果。
该方法基于提出高阶DPA方式的文献,在理论上确实能够适用于掩码实现的加密算法,且在实验中取得了部分效果。但其劣势则更加明显,算法在时间复杂度上呈指数形式,攻击成本过大,因为利用到的相关系数在理论上并不大,导致实际攻击中的成功率较低。
4.2. 二阶模板攻击
高阶DPA攻击的缺点来源于其无训练的攻击方式。因此,使用有训练的高阶模板攻击,则能在一定程度上弥补2阶DPA的不足。有训练的攻击,其优势在于训练集中已知掩码,从而可以找到明确的兴趣点,将兴趣点位置用于之后的攻击过程,能够达到无训练攻击所无法达到的攻击效率,在算法的时间复杂度上也得到了改善。
在训练阶段,需要将能量迹样本分为训练集和测试集两部分,目的是通过测试集验证来防止训练出现过拟合现象。在第1章中提到,模板攻击中的模板实质上为分类器,因此,在正式训练开始之前,还需确定分类目标。在8位的加密设备中,密钥和掩码均未知且都存在256种可能性取值。以次目标的全排列作为分类目标则会导致存在65,536个模板,换句话说,该分类算法不具有可行性。所以,需要通过加掩实现的部分理论来预测更加精简的能量泄漏模型。
目前对加掩密码算法的高阶模板攻击的主要方法是,根据训练数据中已知的各能迹的掩码,计算各掩码的模板。这样,就成功地将模板的数量降低到了256个。若以掩码的汉明重量为能量泄漏模型,则又能再次将模板的数量降低到9,大大提高了攻击的可行性。
攻击阶段中,首先采用模板攻击,计算攻击能迹的掩码,因为S盒所涉及的加掩特性,使得
,在掩码已知的情况下可以轻松的将加掩实现中的中间值全部还原为未加掩的中间值,之后就可以采用一阶DPA来对其进行攻击了。
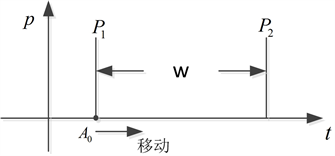
Figure 2. 2-order DPA attack algorithm diagram
图2. 2阶DPA攻击算法示意图
5. 实验过程及结果分析
我们采用加掩AES算法中得到的10,000条能量轨迹作为实验样本,并将其中8000条能量迹作为训练集,剩余2000条能迹作为测试集。
在训练阶段,我们的目标是通过训练集中的数据,求出各个模板中参数。模板共有9个,分别对应掩码汉明重量为0至8的能迹。利用到经典模板攻击模型,假设攻击目标符合多元正态分布。则,每个模板中需要的参数为均值向量m的协方差矩阵C。由于训练集中已知掩码,我们可以很轻松的根据掩码的汉明重量值,将训练集样本分为9个集合,分别对应于9个模板。然后,我们需要针对于每个模板和对应的样本进行参数m和C的计算。
当所有模板参数计算完毕,则训练阶段结束,并进入攻击阶段。从本质上来看,攻击阶段则是攻击者利用每个模板中的特征和从被攻击设备中获得的能量迹来确定该能迹对应于哪个模板,即分类问题。这意味着要使用到每个模板的(m, C)和测试集中的能量迹来计算多元正态分布的概率密度函数 [5] 。也就是说,从给定一个被攻击设备的能迹t和一个模板h = (m, C),计算如下概率:
.
该概率密度函数为统计学中的先验概率,即根据以往经验和分析得到的概率。使用到该公式可通过计算概率的方式用以预测能迹t与模板h的匹配程度,其使用前提为假定攻击目标满足多元正态分布。对应的理论依据为 [5] 中所提及的能量泄漏模型。
同理,使用该方法对一条能量迹在每一个模板中进行计算,将每个模板所对应的概率p进行比较,则正确的模板将与最大的概率相对应,即概率值的大小反应了模板与给定能量迹的匹配程度。将攻击结果与测试集中正确的掩码值进行对比,则能够验证该方案的可行性和成功率。
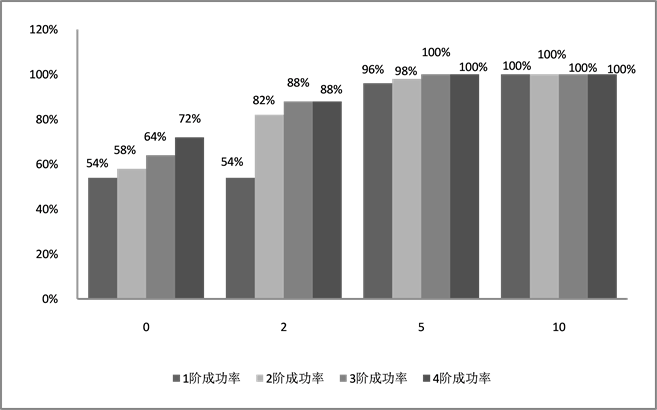
Figure 3. 2-order DPA and 2-order template attack success rate comparison schematic diagram
图3. 2阶DPA与2阶模板攻击成功率对比示意图
基于上述算法,编写Matlab程序对该掩码实现做训练及攻击测试。并统计在不同条件下的攻击成功率。同时,采用2阶DPA攻击方式在同等条件下对能量迹进行攻击,将其成功率与2阶模板攻击进行对比。实验结果如图1所示。其中,横轴为攻击中采用兴趣点的数量,兴趣点为0则代表无须寻找兴趣点的2阶DPA攻击方案,其余部分代表2阶模板攻击方案。每条柱状图中的4个系列则分别代表不同阶的攻击成功率,n阶攻击成功即为攻击目标的正确值处于攻击预测的前n位之内。我们将攻击测试次数记
为
,n阶攻击成功次数记为
,则n阶攻击成功率
为:
。
从图3中我们可以看出,随着兴趣点数数量的提升,有训练的2阶模板攻击在成功率方面已完全优于无训练的2阶DPA攻击。且当兴趣点数量增加到10之后,2阶模板攻击的1阶成功率已达到100%,证明了该攻击方案可以有效的攻破加掩实现的密码算法。
6. 结论
本文基于加掩实现和高阶DPA攻击的理论,着手于有训练的攻击相对于无训练攻击的优势所在,对高阶模板攻击的模型及算法进行了研究,并通过实验部分验证了其可行性。但是,模板攻击自身也存在缺陷,例如多元正态分布中的协方差矩阵经常为病态的,即不可求逆。而DPA攻击中同时也存在自身的优势。因此,今后的研究我们将致力于结合模板攻击的有训练性,以及DPA攻击的优势,探讨有训练的DPA攻击方式。
NOTES
*通讯作者。