镜面映像法确定FCC和BCC晶体始滑移系的原理及技巧

The Principle and Skill of Mirror Image Method for Determining Initial Slip System of FCC and BCC Crystals

摘要: 立方晶系标准投影图是镜面映像法确定面心立方和体心立方晶体始滑移系的必备工具。本文在简单介绍立方晶系标准投影图绘制的基础上，着重分析了镜面映像法的原理，以证实该法的科学性；还举例介绍了用镜面映像法确定晶体始滑移系的技巧。

Abstract: The standard projection of cubic crystal system is a necessary tool for determining the initial slip system of the face-centered cubic (FCC) crystal as well as the body-centered cubic (BCC) crystal by the mirror image method. In this paper, based on the brief introduction of drawing of the cubic crystal system (001) standard projection, the principle of the mirror image method was analyzed to prove the scientific nature of the method, in an addition, the skill for determining the initial slip system of FCC and BCC crystals by the mirror image method was introduced.

1. 引言

单晶体在某一方向受力时，不同取向的滑移系上的分切应力大小可能不同。具有最大分切应力的一个或几个滑移系最先开始滑移，称之为始滑移系。

对于最常见的面心立方和体心立方单晶体，确定其始滑移系的常用方法有两种 [1] [2] [3] ：计算比较法，镜面映像法。计算比较法需要计算可能的12个滑移系的分切应力，然后比较它们的大小，从而确定出始滑移系。由于该法计算量较大，常常也采用镜面映像法。镜面映像法是一种图解法，相对较为快捷。然而，目前尚未发现对其原理的阐述，故一般误以为它仅仅是一个经验规律，质疑其科学性。另外，在运用镜面映像法的过程中，很多读者会遇到一些困难，不知该如何解决。

针对存在的上述问题，本文尝试分析镜面映像法的原理，并结合举例，介绍镜面映像法运用中的一些技巧，以飨读者。

2. 立方晶系标准投影图的绘制

镜面映像法的含义是，在标准投影图中利用镜面映像来确定始滑移系。因此，立方晶系的标准投影图是必不可少的工具。所谓立方晶系的标准投影图，就是仅给出晶体的低指数晶向(<001>、<011>、<111>)和晶面({001}、{011}、{111})的极射赤面投影图。

按照下述方法可以绘制一幅精准的标准投影图：如图1所示，第一步“搭架子”，以o点为圆心、oa为半径画圆，作4条直径均分该圆；分别以图中a、b、c、d四点为圆心，ab为半径在圆内画四段弧线。第二步“填指数”，如将o点定为001，按照右手坐标系定a点为100，则b点为010；根据晶体对称性及晶带定理，图中其它各点指数可以确定，如e = a + b = 100 + 010 = 110，j = o + e = 001 + 110 = 111，依此类推。当然，如果只是供定性分析用，大可不必将“架子”搭得那么精准，徒手画出即可。标准投影图是以基圆圆心的指数命名的，如，图1称作立方晶系(001)标准投影图。

由图1可见，立方晶系标准投影图由24个三角形构成，称之为取向三角形。虽然每个取向三角形所代表的晶体取向范围不同，但它们的三个顶点的指数类型是相同的，分别是：001型、011型、111型。每个取向三角形都可以用它三个顶点的指数表示，如， $001-0\bar{1}1-1\bar{1}1$ 。

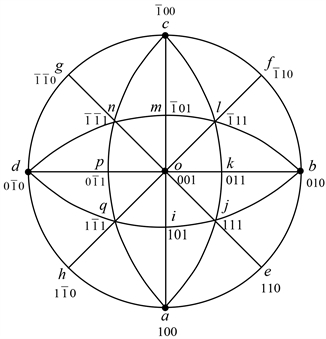
Figure 1. Drawing of the cubic crystal system (001) standard projection

图1. 立方晶系(001)标准投影图的绘制

3. 镜面映像法的原理

镜面映像法的要点是，在立方晶系标准投影图中，以力轴所在取向三角形的与晶体滑移面指数类型相同的那个顶点的对边为镜面，该顶点的镜面映像就是始滑移面；以力轴所在取向三角形的与晶体滑移方向指数类型相同的那个顶点的对边为镜面，该顶点的镜面映像就是始滑移方向。以力轴在[123]的面心立方单晶体拉伸为例，面心立方的滑移面为{111}，滑移方向为<110>。由图2可见，力轴123位于取向三角形001-011-111内(如何确定力轴的位置将在后面介绍)。以取向三角形的111顶点的对边001-011为镜面，111顶点的映像是 $\bar{1}\text{11}$ ，即始滑移面为 $\left(\bar{1}11\right)$ ；以三角形的001-111边为镜面，011顶点的映像是101，即始滑移方向为[101]。故该始滑移系为 $\left(\bar{1}\text{11}\right)\left[101\right]$ 。

对每个可能的滑移系，定义力轴与滑移面法线的夹角为 $\phi$ ，力轴与滑移方向的夹角为 $\lambda$ ，则作用在滑移系上的分切应力为：

$\tau =\sigma \cos \phi \cos \lambda$ (1)

式中， $\Omega =\cos \phi \cos \lambda$ 称作施密特因子或取向因子。施密特因子最大的滑移系就是始滑移系。

众所周知，和为定值的两个数，这两个数之差越小，则两数之积越大，当这两个数相等时，其乘积有最大值。例如，a + b = 10，1 × 9 = 9，2 × 8 = 16，3 × 7 = 21，4 × 6 = 24，5 × 5 = 25。

由于 $\phi +\lambda \ge {90}^{\circ }$ ， $0<\phi <{90}^{\circ }$ ， $0<\lambda <{90}^{\circ }$ ， $\phi$ 与 $\lambda$ 的值越是接近， $\Omega$ 值越大； $\phi$ 与 $\lambda$ 的值相差越大， $\Omega$ 值越小；当 $\phi =\lambda ={\text{45}}^{\circ }$ 时， $\Omega$ 得最大值0.5。

镜面映像法正是遵循了始滑移系的“ $\phi$ 与 $\lambda$ 同时接近中等值”的原理。

在投影图中， $\phi$ 角的大小就是图中表示力轴方向的点与表示滑移面法线方向的点之间的夹角， $\lambda$ 角的大小也类似。要精确测量图中两个点间的夹角，需要用到特定的测量工具——乌氏网，具体的测量方法参见资料 [1] [2] [3] [4] 。镜面映像法并不要求用 $\phi$ 或 $\lambda$ 的精确值进行比较，只需在图中通过定性比较选择出同时接近中等值的 $\phi$ 与 $\lambda$ ，所以姑且定性地用图中两个点之间的直线距离远近来近似代表它们之间夹角的大小。以图2中力轴在123点为例，定性地比较一下力轴[123]分别与四个可能的滑移面(111)、 $\left(\bar{1}11\right)$ 、 $\left(\bar{1}\bar{1}1\right)$ 、 $\left(1\bar{1}1\right)$ 之间的夹角 $\phi$ ：(111)与[123]的夹角太小，而 $\left(1\bar{1}1\right)$ 以及 $\left(\bar{1}\bar{1}1\right)$ 与[123]的夹角都太

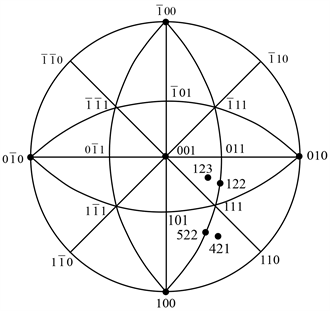
Figure 2. Determination of the initial slip system of the face-centered cubic crystal in the cubic crystal system (001) standard projection by the mirror image method

图2. 用镜面映像法在立方晶系(001)标准投影图中确定面心立方晶体的始滑移系

大， $\left(\bar{1}11\right)$ 与[123]的夹角比较适中。如果 $\left(\bar{1}11\right)$ 是始滑移面，则在 $\left[0\bar{1}1\right]$ 、[101]、[110] 三个可能的始滑移方向中，[101]与[123]的夹角与 $\left(\bar{1}11\right)$ 和[123]的夹角差不多相等。故始滑移系应当是 $\left(\bar{1}11\right)$ [101]，这与计算比较法所得结果相同。

4. 镜面映像法的运用技巧

正确确定力轴在标准投影图中的位置，是正确确定始滑移系的前提条件。对于每个取向三角形，力轴的位置无非三种：在顶点，在边上，在内部。当力轴位于取向三角形内部时，始滑移系只是晶体中的一个滑移系；当位于一条边上时，由于力轴为其两侧的两个三角形所共有，故始滑移系是晶体的两个等价的滑移系；同理，当位于三角形的一个顶点时，始滑移系是晶体的四个等价的滑移系(力轴位于011型顶点)，或六个等价的滑移系(力轴位于111型顶点)，或八个等价的滑移系(力轴位于001型顶点)。

可以用矢量分解的方法确定力轴的位置：以001型、011型、111型指数为单位矢量，将力轴的指数进行分解。从理论上讲，无论怎样分解，最终都能确定力轴的位置，但如果能注意到以下几个问题，将会使确定过程更加便捷：① 力轴指数中绝对值最大的数值就是力轴分解后所得分量的个数；② 每个类型的单位矢量中只能选取一种值，如001型只能选择其6个可取值(001、010、100、 $00\bar{1}$ 、 $0\bar{1}0$ 、 $\bar{1}00$ )中的一种，但所选的这个值可重复使用；③ 分解所得分量中不同指数分量的数目不能超过三个；④ 分解所得分量中不同指数分量就是力轴所在取向三角形的三个顶点，或三角形某条边的两个端点。例如，力轴指数123，可分解为111 + 011 + 001，则123位于111-011-001取向三角形内。理由是，力轴指数123这个矢量是由111、011、001三个单位矢量合成的，根据晶带定理，111 + 011 = 122，它位于111和011所在的晶带，即三角形111-011-001的111-011边上，且在111和011之间，见图2。又，122 + 001 = 123，它位于122和001所在的晶带，且在122和001之间，由图2可知，123位于三角形111-011-001内部。至于123在这个三角形内部的确切位置，对于确定始滑移系并不重要，因为无论力轴在取向三角形111-011-001内的哪一点，晶体的始滑移系都是相同的。如果将力轴123分解为010 + 001 + 011 + 101，这有悖于上述第①、②两点，虽然最终也可由此确定123的位置，但过程就要复杂一些。再如力轴421，

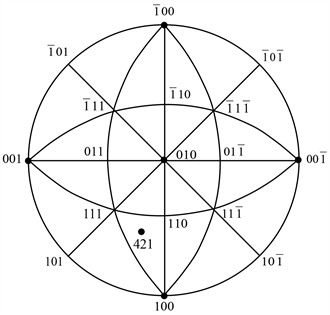
Figure 3. Determination of the initial slip system of the face-centered cubic crystal in the cubic crystal system (010) standard projection by the mirror image method

图3. 用镜面映像法在立方晶系(010)标准投影图中确定面心立方晶体的始滑移系

可分解成111 + 110 + 100 + 100，此处100被使用了两次，可以确定421在111-110-100三角形内，如图2。对力轴522，可分解成111 + 111 + 100 + 100 + 100，由此可以确定522在三角形的111-100边上，见图2。

当力轴位于以一条边与基圆相接的那8个取向三角形中时，如图2，力轴[421]位于取向三角形111-110-100之中，运用镜面映像法时就会遇到麻烦。若晶体为面心立方，根据镜面映像法，始滑移方向为[101]，但始滑移面似乎无法判断，因为111的镜面映像在基圆之外，或者说在基圆的背面，看不到。有三种方法可以解决这类问题。第一种方法，将投影图的基圆圆心指数从001变为010，即在(010)标准投影图中进行操作，如图3所示，就很容易得到始滑移系 $\left(\text{11}\bar{1}\right)\left[101\right]$ 。当然，在(100)标准投影图中进行操作也可以得到相同结果。第二种方法，给(111)的z分量即第三个数加一个负号，即得始滑移面 $\left(\text{11}\bar{1}\right)$ 。其原理是，在图2中，111与它的镜面映像具有相同的x分量和y分量，以及反向相等的z分量。第三种方法，找(111)的中心对称点，由图2可见，(111)的中心对称点是 $\left(\bar{1}\bar{1}\text{1}\right)$ ，即始滑移面为 $\left(\bar{1}\bar{1}\text{1}\right)$ 。其原理是，(111)的镜面映像与 $\left(\bar{1}\bar{1}\text{1}\right)$ 是同一个晶向的两个相反的方向，只不过(111)的镜面映像在投影图的背面，而 $\left(\bar{1}\bar{1}\text{1}\right)$ 在投影图的前面。相比之下，第三种方法最为便捷。当然，各人可以根据自己的具体情况选用其中任意一种方法。

5. 结论

和为定值的两个数，当这两个数相等时其乘积最大。正是基于这一原理，镜面映像法运用立方晶系标准投影图从BCC和FCC晶体多个可能的滑移系中，方便地图解出同时接近中等值的 $\phi$ 和 $\lambda$ ，使其施密特因子 $\cos \phi \cos \lambda$ 具有最大值，从而确定出始滑移系。可见，镜面映像法并非经验之谈。可以用矢量分解的方法确定力轴在投影图中的位置，本文所提的四条建议，可以使这一过程更加便捷。对于力轴所在取向三角形与基圆以一条边相接时，镜面映像法似乎无法运用，本文介绍了解决这一问题的三种方法。

NOTES

^*通讯作者。