环形涵道串列翼空气动力技术的研究

Study on Aerodynamic Technology of Ring Culvert Tandem Plumes

摘要: 本论文在旋翼空气动力原理基础上，提出截取旋翼升力翼尖效应部分桨叶扫掠圆环面、重新串列布置羽翼在涵道内做回转运动的改进思路，形成圆环形涵道内置串列翼空气动力技术方案。该方案涵道宽度接近或超过串列翼翼展，较小的翼尖间距最大限度抑制了串列翼翼尖环流，降低了诱导阻力，从而提升空气动力效率；该方案同时以较小的投影占地面积，解决了升力总面积问题，在较小的运动速度下获得较大的动力输出，提升了系统运输效率。通过重建圆环形涵道内置串列翼空气动力数学计算模型，对比计算分析相同参数孤立机翼、旋翼及圆环形涵道内置串列翼空气动力效率。通过环形涵道串列翼同时具备空气动力效率和运输效率高效、垂直起降性能和超低空安全性能、良好的雷达外形隐形和声学隐形等性能分析，做出环形涵道串列翼空气动力技术，是轴驱动旋翼空气动力的颠覆性技术的结论，同时做出是面向未来空中交通工具技术平台，以及与道路交通工具汽车展开全面竞争并能取得优势的前瞻性展望。

Abstract: On the basis of the aerodynamic principle of the rotor, this paper puts forward an improved idea to intercept the rotor lift wing tip effect part of the rotor blade to sweep round circle and to ar-range the wing in the culvert. The width of the scheme is close to or beyond the wing span of the tandem plumes, and the smaller tip spacing maximizes the suppression of the tandem plumes tip circulation, reducing the induced drag and improving the aerodynamic efficiency. The scheme also solves the problem of the total lift area with smaller projection area, which is larger at a smaller velocity. The power output of the system improves the efficiency of the system transportation. The aerodynamic efficiency of the tandem plume in the same plume, rotor and ring shaped culvert is calculated and analyzed by the reconstruction of the aerodynamic mathematical model of the tandem plumes in the circular culvert. Through the analysis of aerodynamic efficiency and efficient transport efficiency, vertical landing and landing performance and ultra low altitude safety performance, good radar profile stealth and acoustic stealth, the annular culvert tandem plumes is the conclusion of the annular culvert tandem plumes aerodynamic technology, which is the conclusion of the subversive technology of the air power of the shaft driven rotor. It is a forward-looking perspective for future air traffic vehicle technology platform, and comprehensive competition with road vehicles, vehicles and advantages.

1. 引言

固定翼通用航空器运输效率通常在6~18 kg/kw范围，像维珍大西洋环球飞行者号运输效率达到30 kg/kw左右，但翼展34.4米几乎是机身长度的三倍，起降停靠严重依靠机场和跑道，没有便捷性可言。

旋翼飞行器虽然可以不依赖于机场和跑道，具有一定的便捷性，但低下的运输效率，是以巨大的能源消耗为代价实现飞行，不可持续发展。目前锂电池能量密度在0.12~0.18 kw.h/kg，最能检验旋翼飞行器的应用效能。电动旋翼飞行器即使不计结构重量，所有电能全部推动电池重量，也难以超过25分钟滞空时间(旋翼运输效率与锂电池能量密度乘积)。若算上结构重量和载荷，电动旋翼飞行器的实际滞空时间缩短至10分钟左右，加上外置、高速旋转、锋利的桨叶，限制了电动旋翼飞行器的实际应用范围。

未来的空中交通工具，应具有环保、安全、高效、便捷、舒适、智能等性能特征。就像Uber Elevate愿景，飞行器自由停靠在天台、花园、水面，以及像汽车一样停靠在路边，或在城市的建筑物间和森林空间中自由穿行，道路、山川和海峡不再是阻隔。未来的空中交通工具，需要革命性空气动力装备技术来支撑，在未获得革命性空气动力装备技术与之前，这还只是一个梦。

以固定翼和旋翼为代表的通用航空技术，百年来在卡门–加布里埃尔运输效率图中，飞行器效率最高那片区域，留下一片空白。探寻环保、高效、便捷、未来的空气动力装备技术，面向未来，立足当下，具有重要的现实意义。

2. 研究方向

飞行器在功率W (kw)推动下水平匀速运动为v (m/s)，所受重量G (kg)与机翼升力L (N)，推力F (N)和阻力D (N)，大小相等方向相反。飞行器运输效率K (kg/kw)与空气动力效率k关系推导如下：

$K=\frac{G}{W}=\frac{\frac{L}{9.8}}{\frac{F\times v}{1000}}=\frac{\frac{L}{9.8}\times 1000}{\frac{L}{k}\times v}=\frac{102\times k}{v}$ (1)

飞行器运输效率K与空气动力效率k成正比，与运动速度v成反比，K.v为无量纲。

其中公式(1)，飞行器运动速度等于102 m/s (0.3 Ma)时，运输效率K数值等于空气动力效率k(单位为s/m)；飞行器运动速度大于102 m/s (0.3 Ma)时，运输效率K数值小于空气动力效率k，说明飞行器运输效率K最大值存在于机翼0.3 Ma运动速度范围内，这与卡门–加布里埃尔运输效率图中，飞行器效率最高区域那片空白是对应的，这是本项目研究和应用的范围和重点。

其中公式(1)中，飞行器升力L和推动功率W尤其是电功率易于检测，机翼运动速度v同样易于检测和计算，为计算空气动力效率k等不可直接测得的空气动力参数创造了条件。

3. 环形涵道串列翼空气动力原理

在理论上研究绕流物体的升力理论要比研究阻力问题容易得多，那是因为阻力理论必须考虑流体粘性。与此相反，升力却可极近似地用无粘性流理论得到 [1] 。飞行器的空气动力效率，实际上就是机翼升力与阻力的比值关系，阻力包括伴随升力的型阻阻力、诱导阻力和与升力无关的废阻力 [2] 。

水平直线飞行器机翼升力L的大小，与机翼翼型结构影响升力系数C_l相关；与升力面积S_l成正比关系；与运动速度v的平方成正比；低亚音速下，空气密度⍴视为常量。升力L计算公式如下： [1]

$L=\frac{1}{2}{C}_l\cdot \rho \cdot S_l\cdot v^2$ (2)

在速度0.3 Ma以下的低亚音速区域，机翼阻力主要由型阻阻力D_w、诱导阻力D_p组成。型阻阻力的大小与升力影响因素类似，C_d为型阻阻力系数。诱导阻力的大小，与机翼翼型结构、展弦比、升力面积及翼尖运动速度相关，C_p为诱导阻力系数。型阻阻力D_w、诱导阻力D_p计算公式如下： [1]

$D_w=\frac{1}{2}{C}_d\cdot \rho \cdot S_l\cdot v^2$ (3)

$D_p=\frac{1}{2}{C}_p\cdot \rho \cdot S_l\cdot v^2$ (4)

提高飞行器机翼空气动力效率k(升阻比)，实际上就是提高升力系数同时降低阻力阻力系数的过程。在低亚音速区域，忽略摩擦阻力影响，机翼空气动力效率k计算公式推导如下：

$k=\frac{L}{D}=\frac{\frac{1}{2}\cdot C_l\cdot \rho \cdot S_l\cdot v^2}{\frac{1}{2}\cdot C_d\cdot \rho \cdot S_l\cdot v^2+\frac{1}{2}{C}_p\cdot \rho \cdot S_l\cdot v^2}=\frac{C_l}{C_d+C_p}$ (5)

其中，诱导阻力系数C_p，与升力系数C_l的平方成正比，与展弦比λ，机翼修正系数ε (圆形翼0，梯形翼1~3，矩形翼2~5)组成的诱导因子相关。诱导阻力系数C_p计算公式如下： [1]

$C_p=\frac{C_l^2}{\pi \cdot \lambda }\left(1+\epsilon \right)$ (6)

提高飞行器运输效率，实际上就是提高空气动力效率同时降低机翼运动速度的过程。降低飞行器机翼运动速度，意味着升力的减小，需要通过增加机翼总升力面积来与载荷匹配。这个方案对现实固定翼和旋翼飞行器来说，是不可行的。

我们在旋翼的空气动力原理的基础上，尝试对其改进。截取旋翼翼尖圆环形扫掠面，并在扫掠环面中，按照等翼距排列布置小翼展、大展弦比机翼——羽翼，羽翼翼根部串列形成圆环形串列翼。串列翼由翼端和驱动端组成，驱动端作用是固定翼端、支撑和驱动串列翼 [3] ，如下图1。

串列翼空气动力原理实际上是截取了翼尖半径为R、翼根半径为r升力集中的环面，由于存在翼尖速度V_R和翼根速度Vr差，串列翼存在升力翼尖效应。但随着串列翼回转半径的增大，羽翼翼根速度趋近于翼尖速度，其比值趋近于1，串列翼翼尖效应降低。这一规律说明，相同翼尖速度下，串列翼随回转半径R的增加，升力增加趋近于水平直线运动孤立机翼。翼尖速度VR和翼根速度Vr关系推导如下：

$v_r=\frac{r}{R}\times v_R$ (7)

图1中，串列翼扫掠实度为0.26，翼根水平翼距为三倍左右弦长，翼尖水平翼距为4倍弦长以上(考虑到前后翼的影响，是否能进一步增加串列翼扫掠实度，需要实验室验证)；四旋翼扫掠实度0.08。相同半径的串列翼升力总面积达到四旋翼的2.5倍以上，翼尖效应区域面积达到四旋翼的5倍以上。相同投影占地面积下，串列翼总升力面积远远超过固定翼飞行器。较大的升力面积，为串列翼降低运动速度获得较高运输效率，创造了条件。

串列翼羽翼翼展小为内置环形涵道创造了条件，且涵道宽度易实现超过串列翼翼展。环形涵道和串列翼翼尖间距(0.02~0.05倍弦长)，抑制串列翼翼尖环流，为降低诱导阻力创造了条件，如图2。

Figure 1. Tandem plumes and four rotor

图1. 串列翼与四旋翼

Figure 2. Ring shaped culvert tandem plumes

图2. 圆环形涵道串列翼

圆环形涵道串列翼诱导阻力系数C_p与升力系数C_l的平方成正比，与ε (奥德瓦尔斯因子)和 (展弦比)成反比；其计算公式如下： [4]

$C_p=\frac{C_l^2}{\pi \cdot \lambda \cdot \epsilon }$ (8)

源自于对旋翼空气动力原理改进的圆形涵道串列翼空气动力技术方案，具有降低翼尖效应增加升力的性能，也具有抑制翼尖环流降低翼尖诱导阻力的性能，同时还具有较大的总升力面积来匹配较低的运动速度下的载荷。为提升空气动力效率和运输效率创造了技术条件。

串列翼做回转运动，串列翼扫掠过的平面形状可以是圆环形，也可以是胶囊环形，其区别在于串列翼连接的形式。刚性连接的串列翼只适用于圆环形，柔性连接的串列翼适用于各种回转形状，如图3。

同一环形涵道，也可以在垂直方向布置相同串列翼，反向运动。这样较小的涵道投影面积，具有较大的总升力面积，同时解决单组串列翼运动产生的自转。

4. 圆环形涵道内置串列翼空气动力效率计算模型

双翼串列翼相对单翼空气动力效率有增升作用 [5] ，其增升的机理来自于前翼翼尖环流，对后翼的影响。前后翼的翼距和后翼的安装角，对双翼串列翼空气动力效率显得特别重要。

如图2圆环形涵道串列翼，多羽翼数量达到20组。涵道壁的宽度接近甚至超过串列翼羽翼翼展，二者之间的翼尖间距也在0.02~0.05倍弦长范围，涵道壁对串列翼翼尖环流有强烈的抑制作用。串列翼前后翼、以及自身回转运动，在一定时间范围内互为前后翼，在0~0.3 Ma低亚音速速度范围，在涵道壁的影响下，水平前后翼的影响较小，前后翼水平翼距和安装角在圆环形涵道串列翼上并不重要。

在垂直方向的上下反向串列翼组，上串列翼运动产生的、沿涵道轴向旋转向下的气流，与下串列翼的运动结合后，形成一个类似串列翼羽翼前缘气流的下偏转角。垂直反向的下串列翼可以加大攻角，来克服涵道轴流气流的影响。

设定圆形涵道内置串列翼回转圆心0，羽翼翼展为x，羽翼翼根半径为r，翼尖半径为R，翼尖速度为v；羽翼前缘运动速度在羽翼翼展x方向上成线性分布，速度分布函数f(x)与翼尖速度v和翼展x的关系利用公式7推导如下， $x=\in [r,R]$ ；

$f\left(x\right)=\frac{v}{R}\cdot x$ (9)

设定串列翼羽翼平均弦长b，在羽翼展方向微分升力面积∆S；

Figure 3. Capsule ring culvert tandem plumes

图3. 胶囊环形涵道串列翼

$\Delta S_l=b\cdot \Delta x$ (10)

将公式9、10代入公式2，圆环涵道串列翼n个羽翼总升力积分L：

$L={\displaystyle {\sum }_{i=1}^n\left(\underset{r}{\overset{R}{{\displaystyle \int }}}\frac{1}{2}{C}_l\cdot \rho \cdot b\cdot {\left(\frac{v}{R}\right)}^2\cdot x^2\text{d}x\right)}$ (11)

同理，圆环涵道串列翼n个羽翼型阻阻力:

$D_w={\displaystyle {\sum }_{i=1}^n\left(\underset{r}{\overset{R}{{\displaystyle \int }}}\frac{1}{2}{C}_d\cdot \rho \cdot b\cdot {\left(\frac{v}{R}\right)}^2\cdot x^2\text{d}x\right)}$ (12)

圆环涵道串列翼总诱导阻力，在低亚音速下基于无粘计算，将公式8代入公式4，诱导阻力D_p：

$Dp=\frac{1}{2}\cdot \frac{C_l^2}{\pi \cdot \lambda .\epsilon }\cdot \rho \cdot S_l\cdot v^2$ (13)

将公式11、12、13代入公式5，圆环形涵道串列翼升阻比k计算推导如下：

$k=\frac{{\displaystyle {\sum }_{i=1}^n\left({{\displaystyle \int }}_r^R\left(\frac{1}{2}{C}_l\cdot \rho \cdot b\cdot {\left(\frac{v}{R}\right)}^2\cdot x^2\right)\text{d}x\right)}}{{\displaystyle {\sum }_{i=1}^n\left({{\displaystyle \int }}_r^R\left(\frac{1}{2}{C}_d\cdot \rho \cdot b\cdot {\left(\frac{v}{R}\right)}^2\cdot x^2\right)\text{d}x\right)+\frac{1}{2}\cdot \frac{C_l^2}{\pi \cdot \lambda \cdot \epsilon }\cdot \rho \cdot S_l\cdot v^2}}$ (14)

圆环涵道串列翼计算功率P计算推导如下，

$P=F\times v={\displaystyle {\sum }_{i=1}^n\left(\left({\displaystyle {\int }_r^R\frac{1}{2}{C}_d\cdot \rho \cdot b\cdot {\left(\frac{v}{R}\right)}^3\cdot x^{3}dx}\right)+\frac{1}{2}\cdot \frac{C_l^2}{\pi \cdot \lambda \cdot \epsilon }\cdot \rho \cdot S_l\cdot v^3\right)}$ (15)

上述公式计算推导过程，同样适用于旋翼空气动力特征。

5. 圆环形涵道串列翼、旋翼、孤立机翼空气动力对比计算

设定串列翼、旋翼、机翼选用相同翼型结构，展弦比、升力面积，采用NACA6409-li翼型 [6] 。

串列翼：R = 800 mm，r = 400 mm，展弦比λ = 8，平均弦长b = 50 mm，涵道宽度350 mm，翼尖间距3 mm，奥德瓦尔斯因子ε = 5，翼尖速度v = 102 m/s，羽翼20组；

旋翼半径：R = 400，展弦比λ = 8，b = 50 mm，机翼修正系数ε = 1，翼尖速度v = 102 m/s；

孤立机翼翼展：R = 400，展弦比λ = 8，b = 50 mm，机翼修正系数ε = 1，速度v = 102 m/s；

上述翼型在速度102 m/s (0.3 Ma)，10˚C下雷诺数：Re = 358978；在速度68 m/s (0.2 Ma)，10˚C下雷诺数：Re = 239319；在速度34 m/s (0.1 Ma)，10˚C下雷诺数：Re = 119659 (图4)。

圆环形涵道串列翼、旋翼、孤立机翼空气动力对比计算见表1。

6. 圆环形涵道串列翼、旋翼、孤立机翼空气动力数据对比分析

如表1，对圆环涵道串列翼和旋翼的对比计算，可以理解为串列翼截取了半径400 mm至800 mm扫掠圆环中的羽翼，与剩下半径400 mm旋翼扫掠圆环面桨叶，在空气动力上的比较，孤立机翼作为参照。

6.1. 升力数据对比分析

圆环涵道串列翼相对旋翼，翼型、翼展、升力面积和翼尖速度相同。表1，在0.3 Ma速度下，串列翼回转半径增加一倍，与旋翼升力比值增加至1.8。继续增加串列翼回转半径，串列翼升力趋近于孤立机翼，串列翼与旋翼升力比值趋近于3。

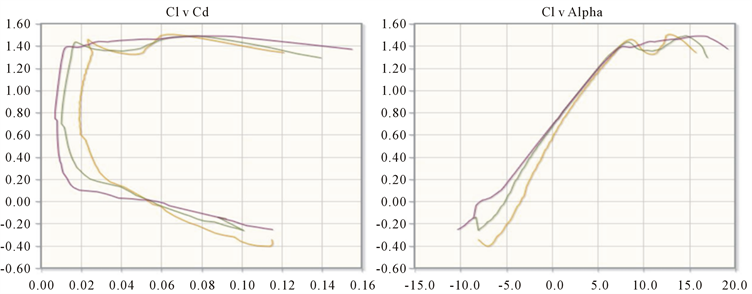注：Re: 100,000橙色，200,000兰色，500,000紫色

Figure 4. NACA6409-li C_dcurve, Cl curve

图4. NACA6409-li阻力、升力系数曲线

Table 1. Summary of aerodynamic comparison calculation

表1. 空气动力对比计算汇总表

注：迎角7°，标准大气压下

规律表明相同条件下，环形涵道串列翼可以通过增加回转半径的方式，降低升力翼尖效应。环形涵道串列翼升力，在不需要增加任何功率消耗的情况下，最高可以接近旋翼的三倍，同时空气动力效率最高接近至旋翼的三倍。

圆环形涵道串列翼，在0.3 Ma翼尖速度、1.6 m直径、0.29扫掠实度下，20组羽翼获得2200 N动力输出，是固定翼和旋翼飞行器无法比拟的。在涵道轴向叠加反桨的串列翼组，将成倍增加总动力输出。环形涵道串列翼在0.3 Ma低亚音速下，获得10 kN、100 kN甚至更高数量级载荷能力，并保持30 kg/kw以上的运输效率是可行的。

6.2. 阻力数据对比分析

表1中，在0.3Ma速度下，孤立机翼和旋翼的诱导阻力占据了重要份额，十倍于型阻阻力，直接影响到空气动力效率和运输效率。圆环涵道串列翼得益于宽度接近串列翼翼展的涵道对翼尖环流的抑制作用，诱导阻力仅为型阻阻力的两倍左右。

6.3. 空气动力效率数据对比分析

表1中，在0.3 Ma速度范围内，空气动力效率与速度的增减变化不大，这可能源自于系数取值的误差，实际上是存在较小的数值差。

圆环形涵道串列翼空气动力效率到达32.7 kg/kw，超过孤立机翼的四倍、旋翼的十倍。旋翼在低亚音速空气动力效率低下的原因，来自于轴驱动方式形成的升力翼尖效应对升力的影响，以及旋翼翼尖环流形成的诱导阻力的影响。

6.4. 运输效率数据对比分析

表1中，圆环形涵道串列翼的运输效率，在0.3 Ma翼尖速度时达到32.7 kg/kw，在0.2 Ma翼尖速度时达到51 kg/kw，分别超过孤立机翼的四倍、旋翼的十倍。

道路交通工具汽车在100 km时速下，运输效率通常在22 kg/kw。圆环形涵道串列翼技术，形成的飞行器在0.3 Ma翼尖速度范围内，在相同100 km运动时速下，其运输效率超过道路交通工具汽车。

将表1中的升力、升阻比、计算功率，带入公式1，计算得出串列翼、旋翼的运输效率和空气动力效率相对应的是翼尖速度。串列翼的翼尖速度可以通过转速计算，也可以用测速仪直接测得，串列翼输入电功率也可以用仪表直接测得，串列翼升力也可以用测力计直接测得，从而计算出该速度下串列翼的空气动力效率，以及串列翼阻力等重要参数。为进一步分析改进环形涵道串列翼空气动力效率，创造条件。

6.5. 数据误差分析

表1中圆环形涵道串列翼、旋翼、孤立机翼空气动力计算数据，其计算数据误差来自于空气动力数学计算模型本身和其中系数的取值精确性。

其中，圆环形涵道串列翼空气动力计算过程中，羽翼安装角趋于一致，水平翼距直接确定为前后翼翼尖距为4倍弦长 [5] ，形成1.6 m直径20组羽翼的串列翼，基本忽略前后翼的影响。

空气动力数学计算模型和其中系数的取值造成的数据误差，可以通过进一步理论计算数据和实验室数据来验证。

在理论计算上，通过欧拉公式来实现圆环形涵道串列翼空气动力特性三维建模仿真计算，能够减少表1中数据的计算误差，同时解决串列翼前后羽翼水平翼距及垂直翼距对空气动力效率的影响关系。

在实验室检测数据验证上，建立电磁驱动串列翼空气动力装置 [3] ，通过升力L、电功率W、羽翼翼尖速度v的实测数据，来计算验证表1中的空气动力效率k、总阻力D等各项空气动力数据；验证前后翼水平翼距，对空气动力效率k的影响，从而确定最佳串列翼扫掠实度范围；验证同涵道上下串列翼组，对空气动力效率k的影响，从而确定上下串列翼最佳安装角及扫掠实度。

7. 圆环形涵道串列翼飞行性能分析

圆环形涵道串列翼运输效率超过所有通用航空飞行器和道路交通工具汽车，相同条件下滞空和续航时间到达旋翼的10倍，滞空和续航能达到数小时，并具有旋翼一样的垂直起降飞行性能。圆环形涵道串列翼也适合电磁驱动，作为垂直起降的、纯电驱动的运输工具，具备实际应用价值。

圆环形涵道串列翼结构中空、外有涵道壁，与飞行器机体完全融合成扁平碟形，能大幅度降低飞行器高度，外形可视度及雷达隐身性能良好。

圆环形涵道串列翼0.3 Ma低速运行噪音，受涵道壁遮挡，声学隐身性能良好。

圆环形涵道串列翼运动部件串列翼内置于涵道中，免于周围物体对飞行安全性的致命影响，也避免对周围人和物体，造成旋翼那样的高速打击伤害。适合城市、森林等复杂空域，以及与人群零距离亲密接触，超低空安全性能良好。

圆环形涵道串列翼所具有的垂直起降、超低空安全等飞行性能，以及外形及声学物理特征，同样是便捷空中交通工具必须具备的基本特征。

8. 结论与展望

本论文通过飞行器运输效率和空气动力效率的公式推导，以及对圆环形涵道串列翼与旋翼和孤立机翼空气动力效率对比计算，得出以下结论：

1) 飞行器机翼在0~0.3 Ma速度范围内运行，是获得运输效率高效的关键。

2) 环形涵道串列翼空气动力效率和运输效率高效，投影占地面积小且输出动力强悍，具有垂直起降和良好超低空安全飞行性能，是轴驱动旋翼空气动力的颠覆性技术。

3) 环形涵道串列翼空气动力技术飞行器作为空中运输工具，在运输效率和运输便捷性上，全面超越道路交通工具汽车成为可能。

4) 其中空气动力模型公式推导计算以及系数取值，串列翼水平翼距及扫掠实度范围，串列翼组垂直翼距范围和对下串列翼组的影响，需要三维建模仿真计算和实验室数据进一步验证。

本论文就环形涵道串列翼高效的空气动力效率和运输效率、垂直起降性能，良好的超低空安全性能、雷达外形隐形和声学隐形性能分析，做出以下展望：

1) 未来的空中交通工具在环保、高效、安全、便捷、智能、舒适方面的性能要求，毋庸置疑需要革命性的空气动力技术平台来支撑和实现。而环形涵道串列翼空气动力飞行器技术平台，正是面向未来空中交通工具的理想选择。

2) 基于环形涵道内置串列翼空气动力技术的飞行器，有望在未来与道路交通工具汽车展开全面竞争并能取得优势。

致谢

本论文编写过程，在对涵道对旋翼空气动力效率的影响及计算中，参考杨超《新概念涵道旋翼飞行器总体设计技术研究》论文相关研究成果；在分析考虑串列翼前后翼的影响，参考程浩《串列翼布局巡飞器气动特性及最优气动布局研究》论文相关研究成果；以及所有对本论文的建议和帮助，特此感谢！