高强螺栓钢管柱端板节点在循环荷载作用下的F-δ曲线函数模型研究

Performance Investigation on F-δ Curve Function Model of End Plate Connection with High-Strength Bolts under Cyclic Loading

摘要: 为了建立高强螺栓钢管端板节点在循环荷载作用下的F-δ曲线函数模型，采用四种常用的函数模型结合实测数据进行了计算，分析了各函数曲线的拟合程度。结果表明：采用多项式函数模型能较好的还原试件实际的F-δ曲线，对数函数模型对试件弹塑性阶段的曲线拟合要优于其他函数。

Abstract: In order to establish the F-δ curve function model of end plate connection with high-strength bolts under cyclic loading, four conventional function models were used to compute based on measured data and the fitting degree of all function curves was analyzed. The results showed that the poly-nomial function model can fit the actual curve better and the logarithmic function model shows its performance is more effective than other function models at elastoplastic stage.

1. 引言

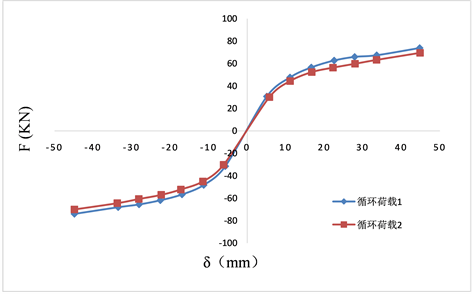
高强螺栓钢管柱端板节点在循环荷载作用下会呈现出非线性和非弹性性质，这也导致其F-δ曲线或是M-θ曲线关系较复杂，因此通过理论得出曲线模型，并以此来描述端板节点的行为显得十分困难。目前，M-θ曲线与F-δ曲线有相通性，国内外学者针对节点性能的研究多基于框架结构连接件试验测试数据，换算得M-θ曲线关系。本文为方便对比，取试验实测数据F-δ曲线来进行对比分析，采用位移控制对三组方钢管进行循环加载，同一位移量级下循环加载两次，加载模型见图1，各试件详细参数见表1，实测F-δ曲线见图2。

2. 常见M-θ曲线模型函数

2.1. 线性函数模型

线性函数模型是最简单，但同时也是最不精确的一种近似模拟曲线模型，实际操作中使用较少。目前常见的线性函数模型有单刚度线性函数模型、双线函数模型、折线函数模型三种 [1] ，具体特点如下：1) 单刚度线性函数模型的主要特点是通过计算求得连接件的初始刚度K₀，以此来代表完整循环加载下连接件的连接特性，优点是计算简单，容易模拟曲线，缺点是循环加载过程中，弯矩一旦超过连接件的使

Figure 1. Test set-up

图1. 加载示意图

Table 1. Detailed parameters of specimen

表1. 试件详细参数

注：G代表高强螺栓试件；t为钢管柱壁厚，mm；g为螺栓孔横向间距，cm；b为钢管柱截面尺寸，mm。

(a) 试件G-8-6-15 (b) 试件G-8-6-20(M12) (c) 试件G-8-6-20(M16)

Figure 2. Load displacement curve of all specimens

图2. 各试件荷载-位移曲线

用极限，该函数模型便失效；2) 双线函数模型的特点是当M-θ曲线中弯矩出现明显转折时，该函数模型可用一条直线代替M-θ曲线的初始斜率。其优点是使得模拟曲线更简洁，便于后续研究，缺点是该函数模型趋于理想化，对于初始斜率较为复杂的连接件而已，该函数模型不能完全反映M-θ曲线真实情况，难以用于实践；3)折线函数模型的特点是用多段(通常为3段或3段以上)直线组合而成的折线近似模拟出连接件的M-θ曲线，优点是操作简单，可以清楚的反映出M-θ曲线的实际走向，但缺点是精确度极低，同时直接与直线的交点突出，使得模拟曲线与实际情况差别较大。

2.2. 多项式函数模型

多项式函数模型由Frye和Morris在1976年首次提出，核心思想是用一个齐次的多项式函数来模拟M-θ曲线，其基本形式如下 [2] ：

$\theta =C_1{\left(KM\right)}^1+C_2{\left(KM\right)}^3+C_3{\left(KM\right)}^5$ (1)

式中，K是标准化参数，取值与连接件类型、几何尺寸，螺栓孔径大小等因素有关；C₁、C₂、C₃是无量纲的曲线拟合常数，取值与连接件类型有关。

该模型的优点是可以较好的模拟出M-θ曲线的特性，但缺点是在某一个范围内，多项式的性质决定该函数会达到并通过峰值点，曲线的走向将发生改变，如果用曲线的斜率来代表连接件的刚度，那么多项式函数模型模拟出的曲线的斜率就有可能出现负数，也意味着刚度为负数，而这在并不符合实际情况。

2.3. 幂函数模型

幂函数模型是经典的M-θ曲线模型之一，根据参数个数不同，可分为二参数幂函数模型和三参数幂函数模型。

1) 二参数幂函数模型 [3] ：

$\theta =C_1{M}^{C_2}$ (2)

式中，C₁ > 0，C₂ > 1。

该函数模型的优点是可以模拟出较好的曲线，同时也可以克服多项式函数模型中出现负刚度的情况，但缺点是：因为表达式中要求系数C₂ > 1，那么该函数模型不能正确反映连接件节点的初始刚度。

2) 三参数幂函数模型 [3] ：

$\theta =\frac{M}{K_t}\frac{1}{\left[1-{\left(M/M_u\right)}^n\right]}$ (3)

式中，K_t是连接件初始刚度；M_u是连接件的极限抗弯承载力；n是曲线的形状参数，数值通过试验数据取值。

该函数模型由Colson和Louvean [3] 提出，它的优点在于其模拟曲线由三个参数K_t、M_u、n共同确定，使得该模拟曲线更加精确，缺点则是该函数模型需要的数据较少，势必导致模拟曲线存在一定的误差，不能完整表达出M-θ曲线的特性。

2.4. 指数函数模型

指数函数模型是另一个经典的M-θ曲线模型，与幂函数模型类似，可根据参数个数不同，可分为三参数指数函数模型和四参数指数函数模型。

1) 三参数指数函数模型：

该函数模型由W.F. Chen [4] 提出，主要用于顶底角钢连接件和带双腹板角钢连接件的M-θ曲线模拟，作者通过试验验证，该函数模型可以较好的模拟出上述两种连接的M-θ曲线特性。其表达式为：

$\frac{M}{M_U}=n\left[\ln \left(1+\frac{\theta }{n{\theta }_0}\right)\right]$ (4)

式中，M_u为理想的弹塑性机构弯矩；R_ti为初始转动刚度；n为曲线的形状参数，数值通过试验数据调整求得；θ为梁对柱的相对转角；θ₀为初始相对转角，其公式为： ${\theta }_0=M_u/R_{ki}$ 。

2) 四参数指数函数模型：

Yoke Leong Yee和Robert E [5] 共同提出了该函数模型，他们研究发现之前提出的指数函数模型表达式多用回归分析得到，并不具备实际的物理意义，因此在试验数据的基础上，用数学方法建立了一种更为全面的指数函数模型，其表达式如下：

$M=M_u\left\{1-\exp \left[\frac{-\left(K_i-K_p+C\theta \right)\theta }{M_u}\right]\right\}+K_p\theta$ (5)

式中，M为梁端真实弯矩；M_u为节点最大弯矩承载力；θ为节点的转角；K_p为应变强化刚度；M_p为节点塑性弯矩承载力；K_i为节点的初始刚度；C为无量纲系数，是一个经验常数目的是控制曲线斜率退化率，其数值需通过试验数据反复调整得到。

该指数函数模型能很好的模拟节点M-θ曲线特性，因为它具有以下优点：

1) 当θ = 0时，M = 0，即曲线通过原点；

2) 当θ = 0时， $\frac{\text{d}M}{\text{d}\theta }=K_i$ ，即曲线在原点的斜率等于节点的初始刚度；

3) 当θ → ∞时， $\frac{\text{d}M}{\text{d}\theta }=K_p$ ，即当θ趋近于无穷大时，曲线斜率等于节点应变强度；

4) 对于任何θ值而言，曲线上该店的斜率都对应相应的节点刚度；

5) 函数模型中的参数均具有明确的物理意义；

6) 函数模型中的参数能够被简单确定，减小了换算过程中误差的产生，使得模拟的曲线更贴近真实情况；

7) 函数模型的表达式简单，便于计算。

3. 曲线的试验研究

本小节对F-δ曲线的研究基于第二章各试件模型的循环荷载试验所得实际的F-δ曲线。通过对各试件模型F-δ曲线使用多项式函数模型、对数函数模型、幂函数模型，以及指数函数模型，总结每一种函数模型的表达式，并对照各个试件模型的曲线函数，从钢管柱壁厚、钢管柱界面尺寸、螺栓规格、螺栓个数，以及螺栓孔横向间距五个方面分析试件模型参量对函数模型表达式中各项系数的影响，最后，比较四种函数模型曲线，根据其对实际F-δ曲线的还原程度，对该四种函数模型进行评价。

3.1. 多项式函数

循环试验的加载方案是同一位移量级加载两次，因此各试件均得到两条F-δ曲线，现对各试件模型的两条F-δ曲线从正向和负向分别使用多项式函数模型进行模拟，得到一个类似的齐次的多项式函数，其表达式为：

$F=C_1{\delta }^2+C_2\delta +C_3$ (6)

式中，F为各位移量级下的真实承载力；δ为试验加载方案的位移量级；C₁、C₂、C₃均为无量纲的系数，表2为各试件模型的多项式函数C₁、C₂、C₃系数表。

从钢管柱截面尺寸和螺栓规格两个方面对各试件模型的多项式函数系数表进行比较可知：

1) 螺栓规格是试件G-8-6-20(M12)和G-8-6-20(M16)之间的唯一变量，前者螺栓规格为M12，后者螺栓规格是M16，从二者系数表可以看出，当提高螺栓规格，系数C₁、C₂和C₃值均增加，其中C₃增加更突出。

2) 钢管柱截面面积是试件G-8-6-25和G-8-6-15之间的唯一变量，前者为钢管柱截面面积是250 × 250 mm，后者钢管柱截面面积是150 × 150 mm，从二者系数表可知，当钢管柱截面面积减小，系数C₁的值减小，C₂和C₃值增加。

3.2. 指数函数

现对各试件模型两条F-δ曲线从正向和负向分别使用指数函数模型，得到一个类似的指数函数，其表达式为：

$F=C_1{\text{e}}^{C_2\delta }$ (7)

式中，F为各位移量级下的真实承载力；δ为试验加载方案的位移量级；C₁、C₂均为无量纲的系数，表3为各试件模型的指数函数C₁、C₂系数表。

从钢管柱壁厚和钢管柱截面尺寸两个方面对各试件模型的指数函数系数表进行比较可知：

1) 螺栓规格与端板节点的指数函数系数有关。从试件指数函数系数表可以看出，当提高螺栓规格，系数C₁的值增大，C₂的值则呈现一定程度的减小；

Table 2. Polynomial coefficient

表2. 多项式系数

Table 3. Polynomial coefficient

表3. 多项式系数

2) 钢管柱截面面积与端板节点的指数函数系数有关。从试件指数函数系数表可知，当钢管柱截面面积减小，系数C₁、C₂的值均增大。

3.3. 对数函数

现对各试件模型两条F-δ曲线从正向和负向分别使用对数函数模型，得到一个类似的指数函数，其表达式为：

$F=C_1\ln \left(\delta \right)-C_2$ (8)

式中，F为各位移量级下的真实承载力；δ为试验加载方案的位移量级；C₁、C₂均为无量纲的系数，表4为各试件模型的对数函数C₁、C₂系数表。

从钢管柱壁厚和钢管柱截面尺寸两个方面对各试件模型的指数函数系数表进行比较可知：

1) 螺栓规格与端板节点的指数函数系数有关。从试件对数函数系数表可以看出，当提高螺栓规格，系数C₁的值增大，C₂的值则呈现一定程度的减小；

2) 钢管柱截面面积与端板节点的指数函数系数有关。从试件指数函数系数表可知，当钢管柱截面面积减小，系数C₁、C₂的值均增大。

3.4. 幂函数

现对各试件模型两条F-δ曲线从正向和负向分别使用幂函数，均得到一个类似的幂函数，其通式为：

$F=C_1{\delta }^{C_2}$ (9)

式中，F为各位移量级下的真实承载力；δ为试验加载方案的位移量级；C₁、C₂均为无量纲的系数，表5为各试件模型的幂函数C₁、C₂系数表。

从钢管柱壁厚和钢管柱截面尺寸两个方面对各试件模型的指数函数系数表进行比较可知：

1) 螺栓规格与端板节点的幂函数系数C₁有关，与系数C₂无关。从试件G-8-6-20(M12)和G-8-6-20(M16)系数表可以看出，当提高螺栓规格，系数C₁的值一定程度地增大，而C₂的值并无明显增大或减小的规律可循；

2) 钢管柱截面面积与端板节点的幂函数系数有关。从试件幂函数系数表可知，当钢管柱截面面积减小，系数C₁和C₂的值增大。

4. 函数模型曲线分析

以试件G-8-6-15为例，图3~图6分别是对该试件的F-δ曲线使用多项式函数模型、指数函数模型、

Table 4. Polynomial coefficient

表4. 多项式系数

Table 5. Polynomial coefficient

表5. 多项式系数

(a) 正向加载 (b) 负向加载

Figure 3. Polynomial function simulation curve of speciment G-8-6-15 (first cyclic loading)

图3. 试件G-8-6-15多项式函数模拟曲线(第1次循环加载)

(a) 正向加载 (b) 负向加载

Figure 4. Exponential function simulation curve of speciment G-8-6-15 (first cyclic loading)

图4. 试件G-8-6-15指数函数模拟曲线(第1次循环加载)

对数函数模型和幂函数模型后得到的相应的函数曲线及表达式。

从图可以看出：

1) 指数函数模型和幂函数模型的函数曲线与试件实际的F-δ曲线差别极大，而多项式函数模型和对数函数模型的函数曲线更加贴近试件实际的F-δ曲线；

2) 在循环加载的作用下，高强螺栓钢管柱端板连接件钢管壁厚或螺栓会经历弹性阶段、弹塑性阶段和塑性阶段，因此实际的F-δ曲线的初始部分可以看作近似的线性关系，此时的斜率为初始刚度，而随着荷载的增加，曲线不能再看成近似线性，此时刚度为变值，故承载力极限状态设计时不能用初始刚度，这是高强螺栓钢管柱端板节点的F-δ曲线重要的特性之一，从四种函数模型的函数曲线比较来看，只有

(a) 正向加载 (b) 负向加载

Figure 5. Logarithmic function simulation curve of speciment G-8-6-15 (first cyclic loading)

图5. 试件G-8-6-15对数函数模拟曲线(第1次循环加载)

(a) 正向加载 (b) 负向加载

Figure 6. Power function simulation curve of speciment G-8-6-15 (first cyclic loading)

图6. 试件G-8-6-15幂函数模拟曲线(第1次循环加载)

对数函数模型的函数曲线将此过程一定程度的还原，即曲线出现明显的线性和非线性区分 [6] ，对于任何δ值而言，函数曲线上该点的斜率都对应相应的节点刚度；

3) 四种函数模型的表达式中，只有多项式函数模型和对数函数模型的表达式较为简单，方便计算，减小了换算过程中误差的产生。

5. 结论

1) 多项式函数模型、指数函数模型、对数函数模型和幂函数模型均能在一定程度上模拟试件实际的荷载—位移曲线，当试件的模型参数发生变化时，各函数模型的无量纲系数呈现规律性的增大或减小。

2) 指数函数模型和幂函数模型计算复杂且不能模拟试件在弹性阶段发生较小位移时的荷载—位移曲线，对于需要计算初始刚度的试件模型建议不采用这两种函数模型。

3) 多项式函数模型能最大程度的还原试件实际的荷载—位移曲线，但弹塑性阶段拟合较差，采用对数函数模型可弥补这一缺陷。