荒漠草原地区典型高速公路平曲线半径对驾驶员瞳孔直径影响分析

Analysis of Influence of Radius of Flat Curve on Driver’s Pupil Diameter in Typical Desert of Desert Steppe

摘要: 相关研究表明驾驶员行车过程中的视觉信息是影响驾驶行车安全的主要因素，而荒漠草原公路由于道路周围环境单调很容易引起驾驶员视觉疲劳，一旦出现公路线形指标突变处极易发生交通事故。为了研究荒漠草原公路长直线段后接平曲线段对驾驶员视觉信息读取及心理负荷的影响，本文选取驾驶员瞳孔直径指标，通过定量描述驾驶员瞳孔直径变化与高速公路平面线形的关系，确定驾驶员心理可容忍的平曲线半径值。首先通过现场试验获得驾驶员在荒漠草原地区典型高速公路下不同平曲线半径下的眼动指标；其次，分析驾驶员瞳孔直径与平曲线半径的相关性；最后，建立自由流下在荒漠草原地区典型高速公路平曲线上行车时，车速、半径和瞳孔直径之间的回归模型。结果表明：平曲线半径与驾驶员瞳孔直径有明显的相关性。应用拉格朗日中值定理发现，当平曲线半径R > 3354 m时驾驶员瞳孔直径变化显著，即为驾驶员瞳孔直径变化的关键点。

Abstract: Relevant studies have shown that visual information during driver’s driving is the main factor af-fecting driving safety, and desert road due to the monotony of the surrounding environment of the road can easily lead to visual fatigue of the driver. Once there is sudden change of the road linear in-dex, it is prone to traffic accidents. In order to quantitatively describe the correlation between pupil diameter changes of the driver and the plane line shape of the highway, the influence of the radius of the freeway flat curve on pupil diameter of the driver is studied based on the eye movement test. Firstly, the eye movement index of the driver under different level curve radius under the typical expressway in the desert steppe is obtained through experiments; secondly, the correlation between pupil diameter and level curve radius of the driver is analyzed; finally, the typical high speed under the free flow in the desert grassland region is established. The regression model is between vehicle speed, radius, and pupil diameter when the road is on a flat curve. The results show that there is a clear correlation between the radius of the flat curve and the pupil diameter of the driver. Using Lagrange’s mean value theorem, we found that when the radius of the flat curve R > 3354 m, the driver’s pupil diameter changes significantly, which is the key point of pupil diameter change.

1. 引言

驾驶员在高速公路上行车，会受到沿线各种来自道路条件、交通条件等方面的刺激。如遇到半径偏小的平曲线时、超越道路前方的车辆时，驾驶员都会感觉心理紧张。从心理学、生理学等研究成果中得知 [1] [2] ：人在从事某项工作时，身心适当的紧张有助于精力、注意力等的集中，从而使工作的效率和可靠度提高。但如果紧张过度，或紧张达到一定程度后持续较长时间，则人或者会因紧张超过生理极限而出现动作失误，或者会因疲劳而使动作出现偏差。引申到驾驶员在道路上行车，在上述两种情况下就较容易出现安全问题。

本文依据人在外界刺激下心理紧张影响瞳孔直径变化 [3] [4] [5] ，所以使用眼动仪来获取驾驶员的瞳孔直径变化，并结合GPS等仪器获得行车速度，定量地研究驾驶员在高速公路上行车时的瞳孔直径变化与平曲线半径、车速等之间的关系，研究与设计车速相对应的高速公路最小平曲线半径。

2. 试验方案

2.1. 试验仪器

如图1所示，试验仪器采用瑞典生产的Tobii Pro Glasses 2眼动仪，记录各驾驶员的眼动指标及行车录像。实时计算出眼珠的水平和垂直运动的时间、位移距离、速度、注视位置及瞳孔直径，眼动仪每秒采集50帧图像，特殊应用时可以有更高的采样率。

2.2. 被试人员

根据试验目的，在行车试验的驾驶员方面选择健康、驾车反应正常、技术较熟练的驾驶员，且行车试验的驾驶员数应达到一定的样本量。本次行车试验中共随机挑选6名不同驾龄驾驶员做试验对象进行

室外试验，他们均为试验路段现场随机取定，且视力均正常或矫正正常，被试者无腰腿病史，也没有心血管病史，驾驶时休息良好。具体受试者信息如表1所示。

2.3. 试验路段

如图2所示，试验路段要选择有丰富线形，路面平整坚实、视距良好、路面、路肩满足规范要求且全路段一致、交通安全状况不乐观的高等级公路路段。考虑到试验目的，选择交通量较小的时段，尽可能保证试验路段交通流状态是自由流，以减小其他车辆及其他环境因素对试验车驾驶员的干扰。根据上述要求，选择了5条宁夏境内典型试验路：京藏高速公路、定武高速公路、青银高速、银川绕城高速公路和国道110线(银川段)。

2.4. 试验流程

在试验前，对驾驶员基本信息和安全性倾向进行问卷调查。根据仪器操作规范，让驾驶员正确佩戴眼动仪并固定好在驾驶员身上，调试正常。试验过程中眼动仪自动记录相应眼动参数数据，同时测量驾驶员行车过程中的生心理数据；试验人员随车记录里程桩号和时间。

根据预先设定好的命名规律，输入文件名号、驾驶员编号及试验道路名称，保存该驾驶员的试验数据。

2.5. 样本数据采集

在自由流下，让6名驾驶员通过一段设计车速为100 km/h、纵坡较平缓、包含有各种半径平曲线的379 km长的路段。在行车途中，分别应用手持GPS检测行车速度、用眼动仪检测驾驶员行车瞳孔直径，

Figure 1. Experimental instruments and subjects

图1. 实验仪器和被试人员

Table 1. Basic information of test personnel

表1. 试验人员基本资料

并用秒表(与GPS时间一致)记录开始时间、车辆行驶起终点时间、车辆经过沿线里程桩时间。在上述行车试验数据中，提取自由流下车辆行驶到各种半径平曲线上时的平均车速和平均瞳孔直径，最终得表2所示的自由流下6名驾驶员驾车在各种半径平曲线上行驶时的平均车速、平均瞳孔直径与平曲线半径间的对应样本数据。

3. 自由流下行车时瞳孔直径、车速和平曲线半径间的关系分析

3.1. 相关性分析

为研究驾驶员在曲线段行车时，瞳孔直径与平曲线半径、行驶车速的相关性，结果如表3所示，通过SPSS软件对曲线路段的驾驶员的眼动指标与曲线段行车的各因素进行相关性检验，如表3所示，通过观察瞳孔直径(D)、行驶速度(V)与平曲线半径(R)之间的相关关系，发现瞳孔直径(D)与平曲线半径(R)、行驶速度(V)的pearson的相关系数分别为0.407、0.248。

Figure 2. Test section site map

图2. 试验路段现场图

Table 2. Sample data of pupil diameter-flat curve radius-vehicle speed while the vehicle is driving

表2. 车辆行驶时瞳孔直径–平曲线半径–车速的样本数据

Table 3. Curve section of the parameters of the correlation test table

表3. 曲线段行车各参数的相关性检验表

3.2. 模型假设

根据前人研究，定性分析可知 [6] [7] [8] [9] ，当车辆在平曲线上行驶时，半径越小，驾驶员心理越紧张，瞳孔直径越大，即瞳孔直径D与平曲线半径R间成反比关系；同理，车辆在行驶过程中，车速越大，驾驶员心理越紧张，瞳孔直径越大，即瞳孔直径D与车速V间成正比关系。本文假设瞳孔直径与车速的b₁次方成正比、与平曲线半径的b₂次方成反比。

再次，据表2的样本数据，可得瞳孔直径与平曲线半径、车速之间各自的散点图。如图3、图4所示，两图能大致反映R-D、V-D之间的关系。根据图3可见，当车辆分别以80 km/h和以100 km/h通过一个半径为800 m的平曲线时，驾驶员的瞳孔直径值显然是不一样的。所以图3、图4中的散点趋势并不能准确反映D和R、D和V的关系，而只能大致反映它们之间的关系。

根据上述分析，同时也考虑到利于用回归方法拟合样本数据，所以最终假设三参数的关系模型为：

$D=b_0\frac{V^{b_1}}{R^{b_2}}$ (1)

式中，D为车辆通过平曲线时驾驶员平均瞳孔直径，mm；V为车辆通过平曲线时的平均车速，km/h；R为平曲线半径，m；b₀、b₁、b₂为回归系数。

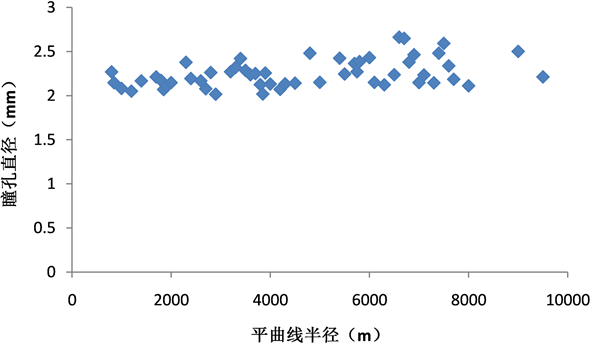
Figure 3. Flat Curve Radius and Pupil Diameter Scatterplot

图3. 平曲线半径与瞳孔直径散点图

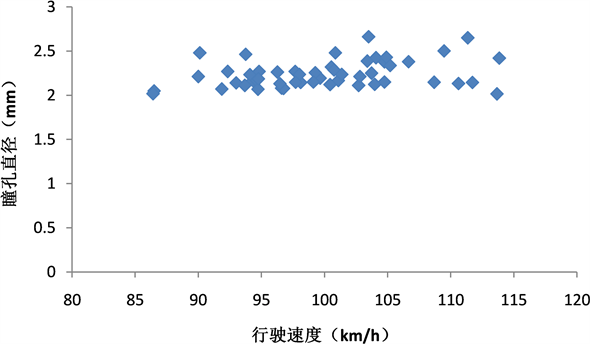
Figure 4. Speed and pupil diameter scatter plot

图4. 车速与瞳孔直径散点图

3.3. 模型建立

据表2中的样本数据，应用多元非线性回归方法，可确定式(1)中的系数b₀、b₁、b₂，最终得三参数的回归模型为：

$D=1.763\frac{V^{-0.028}}{R^{-0.044}}$ (2)

如表4、表5所示：F统计量的相伴概率p₁ = 0.005，小于显著水平a₁ = 0.05，在0.05的显著水平下，回归模型具有一定的统计学意义，可以用此回归模型描述驾驶员行驶速度和曲线半径与瞳孔直径之间的关系。通过检验可以发现b₀，b₁，b₂的参数均符合sig < 0.05的显著性检验，曲线段瞳孔直径的模型的相关系数为R² = 0.957。模型拟合良好，适用于宁夏高速公路驾驶员瞳孔直径变化模型研究。

4. 瞳孔直径分界点确定

在式(2)中，将设计车速100 km/h带入公式得出公式(3)：

$D=1.55R^{0.044}$ (3)

式(3)中R、D的关系曲线如图5所示。

据拉格朗日中值定理，即：

$\frac{f\left(b\right)-f\left(a\right)}{b-a}=f^{\prime }(\xi )$

算得曲线上斜率与平均斜率相同的点的坐标为：(3354, 2.22)，即R₀ = 3354、D₀ = 2.22。在图5曲线中，当R < R₀时，瞳孔直径增加激烈，而当R > R₀时，瞳孔直径则增加缓慢。这意味着，对行车试验的驾驶员来说，R₀ = 3354是一个临界点，当其驾车通过平曲线时的半径超过此值时，他的心理紧张性明显减小。而且，随着R的不断增大，心理紧张性将急剧减小。

5. 结论

综上，通过本文研究得出以下结论：

Table 4. F-test of the model

表4. 模型的F检验

Table 5. Curve segment model parameter values

表5. 曲线段模型参数值

Figure 5. The radius and pupil diameter curve of a car with a flat curve at the design speed

图5. 在设计车速下于平曲线上行车时半径与瞳孔直径曲线

1) 瞳孔直径可用于定量衡量驾驶员行车时的视觉特性反应状况，从而可用于定量研究车辆沿不同半径平曲线上行驶时心理紧张与半径和车速之间的关系。

2) 当车辆以设计车速100 km/h通过不同半径的平曲线时，与R-D曲线陡缓分界点相对应的平曲线半径为R = 3354 m。这个结果，能为从用路者的心生理特性出发，对宁夏典型高速公路设计中平曲线半径最小值的控制提供理论参考。

基金项目

本论文受助于国家自然科学基金“基于驾驶员视觉特性的沙漠公路长直线段对行车安全影响研究”(51468051)和宁夏交通厅科研项目“以人为本”理念下宁夏典型公路安全评价及安全保障研究资助。