基于堆栈降噪自编码器和LBP的人脸识别算法

Face Recognition Algorithm Based on Stack Denoising Autoencoders and LBP

摘要: 针对传统的人脸识别算法的鲁棒性弱，分类准确率不高，运算速率较慢的缺点，基于局部二值模式(Local Binary Pattern)和堆栈式降噪自编码器(Stack Denoising Autoencoders)模型，提出了一种LBP + SDAE新的人脸表情识别算法。首先，先对图像进行直方图均衡化处理，用LBP提取特征，接着进行尺度归一化处理后用SDAE二次提取特征并且去噪，降维，最后用SVM分类。该方法不仅提高了分类的准确率，而且加快了运算的速率。在数据集Yale上进行验证，表明相对于以前传统的人脸识别算法，它具有更高的准确率和较强的鲁棒性。

Abstract: In view of the weak robustness of the traditional face recognition algorithm, the low accuracy of classification and the slow operation rate, this paper proposes a new LBP + SDAE facial expression recognition algorithm, which is based on Local Binary Pattern and Stack Denoising Autoencoders. First, the image is processed by histogram equalization and the feature is extracted with LBP. Then, the scale normalization is followed by using SDA to extract the feature again, to reduce image denoising and dimensionality. Finally, the SVM algorithm was selected as classifier for the recognition of images. This method not only improves the accuracy of classification, but also accelerates the computation speed. The YALE face database was used to test the proposed method. The experiment results show that it has higher accuracy and robustness compared with the traditional face recognition algorithm.

1. 引言

人脸识别 [1] 技术于20世纪50年代开始研究，就是利用计算机对人脸特征进行学习提取有效个人信息的识别技术，它被广泛应用在实际生活当中，如监控系统，智能支付系统，公安系统，银行安全，个人身份验证等。人脸识别技术的研究，一直被广大学者所关注，也是最热门的研究方向。过去的几十年里，众多学者提出人脸识别的方法有：基于模板匹配的方法 [2] [3] ，基于奇异值特征方法 [4] ，子空间分析法 [5] ，主成分分析(PCA) [6] ，支持向量机(SVM) [7] ，隐形马尔科夫模型 [8] 以及近几年兴起的深度学习(Deep Learning)等等 [9] 。深度学习 [10] 有几大重要模型，如：自动编码器(AE)，受限波尔兹曼机(RBM)，深度置信网络(DBN)，卷积神经网络(CNN)等。近几年，国际上很多项目都将深度学习应用到人脸识别中，例如：Deep Face、Deep ID、Face Net等，都取得了相当高的准确率。但是，对于实际应用中的光照，角度，抖动，模糊，遮挡，分辨率，或者年龄变化，化妆整容等影响，还没有得到根本的解决，仍需继续做更深入的研究。

本文利用LBP和SDAE相结合，提出了一种基于深度学习的人脸识别算法。该算法融合了LBP [11] 算法可消除光照和角度等因素影响以及计算简单，效率高的优点和SDAE [12] 算法快速提取特征，有效去除噪声的优点，既提高了算法分类的准确率，又加快了运算的速率和模型的鲁棒性。

2. 局部二值模式

2.1. 原始LBP算子

局部二值模式(Local Binary Pattern)，简称LBP，是一种用来描述图像局部特征的算子，它具有灰度不变性，旋转不变性，计算简易性等优点以及能够去除光照，角度等的影响，捕捉人脸的容貌和纹理细节的特点，使得其被广泛研究和使用，在人脸识别中至关重要。

LBP的算法思想就是利用局部的结构提取窗口特征，再利用统计直方图取得整体特征。如图1所示，LBP是定义在一个3 * 3的领域内，以中心像素的灰度值为阈值，与其相邻的其余8个像素灰度值作比较，若相邻的像素灰度值比中心的像素灰度值大，则标记为1，否则为0。接着按顺序依次排列，转化成一个8位数的二进制数，相对应的十进制就是中心像素的LBP值。那么，这里的二进制数为01101001，对应的十进制数为105，也就是说这个中心像素的LBP值为105。这个LBP值就表示了图像的局部纹理特征。

2.2. 圆形LBP算子

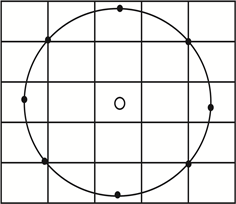
为了使LBP保持灰度不变性和旋转不变性的优点以及适应不同尺寸的区域纹理特征，将正方形邻域替换成圆形邻域，即将3 × 3邻域拓展到任意邻域。改进后的LBP算子允许在半径为R的圆形邻域内有任意多个像素点，符号 $LB{P}_P^R$ 表示在半径为R的圆形邻域内有P个像素点，如图2所示。

通过将图片读取，可以将原始的图像转化为LBP图像。值得注意的是，我们要先将原始的图像划分为若干个子区域，这样每个LBP特征相对应于每个子区域内的每个像素点，然后在每个子区域内建立LBP特征的统计直方图，最后由所有子区域的统计直方图组成整个图像的统计直方图，从而获得图像的所有特征，里面包含了图像的纹理信息。

3. 自编码器的基本模型

3.1. 自编码器

像单隐层这类的浅层神经网络训练能力是有限的，需要消耗大量的时间来获取特征。因此，为了减少训练时间，提出了深度神经网络。其中，自编码器(Autoencoder)就是一种无监督的深度学习方法，它可以从原始的训练数据X里学习得到的特征。

自编码器的基本结构是：输入层，隐层，输出层，如图3所示。输入层的每一个样本 $x_i$ 都来自训练样本 $D=\left\{x_1,x_2,\cdots ,x_{n-1},x_n\right\}$ ，这里的i和n分别是训练样本D中的第i个样本和训练样本D的维数为n。我们把从输入层X过渡到隐层H的这部分叫做编码层，定义为：

$Z=f\left(W_{1}X+b_1\right)$ (1)

其中， $W_1$ 是权重， $b_1$ 是偏置，f是激活函数，Z是获取的特征。

同样的，我们把从隐层H过渡到输出层Y的这部分叫做解码层，定义为：

$Y=g\left(W_{2}Z+b_2\right)$ (2)

其中， $W_2$ 是权重， $b_2$ 是偏置，g是激活函数。

Figure 1. A field of 3 * 3 in LBP

图1. LBP的一个3 * 3的领域

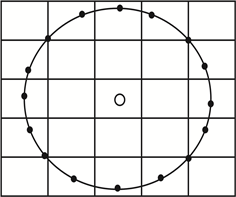LBP₁₆² LBP₈²

Figure 2. A circular field of LBP

图2. LBP的一个圆形领域

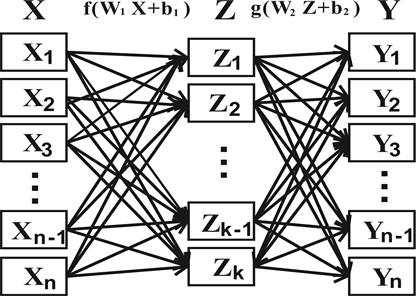
Figure 3. An autoencoder with 1 layer of hidden layers

图3. 隐层数为1层的自动编码器

在自动编码器中，当输入层的结点个数大于隐层的结点个数，这就起到了降维的作用；当输入层的结点个数小于隐层的结点个数，这一般用于稀疏自动编码。编码层的目的是获取特征，解码层的目的就是重构输入层，使输出的Y尽可能的与输入的X对等(即 $X\approx Y$ )。因此，自编码器的主要问题就是找到一组参数 $\theta =\left\{W_1,b_1,W_2,b_2\right\}$ ，使Y (即重构后的X)与原始的X之间的误差足够小。这个参数 $\theta$ 是由反向传播进行调整的，与标准的多层感知机的神经网络训练类似。由于训练样本的不同，我们有很多种计算误差的方法。对于二值神经网络，也就是输入层的每个结点只能取0或1，那么使用交叉熵(Cross Entropy)来定义损失函数，即：

$L\left(x,y\right)=-{\displaystyle {\sum }_{i=1}^n\left[x_i\log y_i+\left(1-x_i\right)\log \left(1-y_i\right)\right]}$ (3)

如果输入的结点是一个任意的实数，则采用平方误差(squared error)来定义损失函数，即：

$L\left(x,y\right)={\Vert x-y\Vert }^2$ (4)

本文采用的是平方误差来定义损失函数，因此自编码器的主要问题可以表示为：

$\min L\left(x,y\right)={\Vert x-y\Vert }^2$ (5)

很多时候，为了防止过拟合，我们一般会在权重添加惩罚因子 $\lambda$ 来控制权重的大小，因此，自编码器的主要问题还可以表示为：

$\min L\left(x,y\right)={\Vert x-y\Vert }^2+\frac{\lambda }{2}{\Vert W\Vert }^2$ (6)

其中，W是 $W_1$ 和 $W_2$ 的组合， $\lambda$ 是正则化系数。

3.2. 降噪自动编码器

由于训练样本的数据量和模型的复杂度等问题，初始的自动编码模型很容易会出现过拟合现象，因此，为了增强自动编码器的鲁棒性，提高模型的泛化能力，Bengio在2008年提出了降噪自动编码器(Denoising Autoencoder)。降噪自动编码器的关键就是在输入层与隐层之间添加噪声处理，具体的网络结构，如图4所示。

在降噪自动编码器中，我们将原始的输入数据X添加噪声变成 $\bar{X}$ ，然后将带有噪声的 $\bar{X}$ 进行自动编码器常规的变换工作。值得注意的是，降噪自动编码仍然是尽量的还原的X，因此它的误差计算是：

$\min L\left(x,y\right)={\Vert x-y\Vert }^2$ (而不是 $\min L\left(\bar{x},y\right)={\Vert \bar{x}-y\Vert }^2$ ) (7)

Figure 4. Denoising autoencoder

图4. 降噪自动编码器

其中，从输入层X到噪声层 $\bar{X}$ 的处理方式有很多，最常用的有两种：mask noise，首先设置一个噪声阈值p ( $0<p<1$ )，每次生成一个浮点数r ( $0<r<1$ )，若满足 $r<p$ ，令 $\overline{x_i}$ 为0，否则令 $\overline{x_i}$ 为 $x_i$ ；Gaussian noise，它满足：

$\overline{x_i}=x_i+Normal\left(0,1\right)$ (8)

与自动编码器对比，经降噪自动编码器训练后的训练数据噪声权重较小，而且在一定程度上训练数据更接近测试数据了。从而，提高了模型的鲁棒性。

3.3. 堆栈自编码器

堆栈自编码器(Stack Autoencoder) [13] [14] 就是将多个自编码器进行叠加，利用上一层的隐层作为下一层的输入层，通过逐层非监督学习的预训练来初始化深度网络的参数，从而提升收敛速度和获取更高级的特征。简单来说，每一个自编码对应于一个隐层。深度网络的第一层就是将原始训练数据作为输入转化成隐层，通过自编码器的训练重构误差最小化来确定其参数；接着将隐层作为下一层的输入，继续通过自编码器的训练重构误差最小化来确定这层参数。以此类推，上一层的隐层都是下一层的输入，并且通过重构误差最小化来确定好每层的参数，这就是堆栈自编码器一个很重要的应用。

如图5所示，利用两个自动编码器构建一个二层的堆栈自编码。首先，第一个自动编码器对应的就是第一层隐层Z，以原始的训练数据作为输入层X，输出层Y为输入层X的重构，通过重构误差最小化，即求最小损失函数获得参数：

$\theta =\left\{W_{11},b_{11},W_{12},b_{12}\right\}$ (9)

接着，第二个自动编码器对应的就是第二层隐层T，以上一层的隐层Z作为输入层，输出层S为输入层 的重构，通过重构误差最小化获得参数 $\theta =\left\{W_{21},b_{21},W_{22},b_{22}\right\}$ 。最后，舍去输出层S，在隐层T后接上SVM分类器，达到分类效果，输出O。堆栈自编码就是从左往右逐层训练每一个自编码器，用训练后的最优参数作为神经网络的初始化参数，完成预训练后还可以通过反向传播算法来调整所有层的参数，这个我们把它叫做“微调”。

考虑到模型的鲁棒性和泛化能力，本文将多个降噪自编码器叠加起来，也就是栈式降噪自编码器(Stack Denoising Autoencoders)。

4. 支持向量机

支持向量机(Support Vector Machine) [15] 是由统计学习理论发展起来的一种机器学习算法，在1995年被Corinna Cortes和Vapnik等人首次提出的，接着在国际上迅速发展并且得到重视。跟以往的算法相比，SVM凸显出许多特有的优势，如：在解决小样本、非线性及高维模式识别中，它能够在很大程度上

Figure 5. Stack autoencoder

图5. 栈式降噪自编码器

解决“维数灾难”和“过拟合”等问题。人脸识别是典型的小样本问题和非线性分类问题，故 SVM在人脸识别中被广泛应用。

SVM的算法思想就是找到一个最优分类超平面，在满足分类要求和分类精度的条件下，使得训练样本和超平面的距离最大化。以两类数据分类为例，假定有训练样本集 $\left(x_1,y_1\right),\left(x_2,y_2\right),\cdots ,\left(x_n,y_n\right)$ ， $x_i\in R^d$ ， $y_i\in \left\{+1,-1\right\}$ ，其中每个样本是d维向量，y是类别标号， $w_1$ 类用+1表示， $w_2$ 类用-1表示。若这些样本是线性可分的，则存在超平面：

$g\left(x\right)=\left(w\cdot x\right)+b=w^{\text{T}}+b=0$ (10)

其中，这里的 $w\in R^d$ 是线性判别函数的权值，b是其中的常数项。

为了使所有 个样本都可以被超平面正确的分开，那么就要满足：

$y_i\left[\left(w\cdot x_i\right)+b\right]\ge 1,i=1,2,\cdots ,N$ (11)

其中， $g\left(x\right)=1$ 和 $g\left(x\right)=-1$ 就是过两类中各自离分类面最近的样本且与分类面平行的两个边界超平面。

因为要限制两类分类面最近的样本 $g\left(x\right)=1$ 和 $g\left(x\right)=-1$ ，所以分类间隔就是 $M=\frac{2}{\Vert w\Vert }$ 。于是，引入一个拉格朗日系数 ${\alpha }_i\ge 0,i=1,2,\cdots ,N$ ，求解最优超平面的问题就转化为：

${\min }_{w,b}{\max }_{\alpha }L\left(w,b,\alpha \right)=\frac{1}{2}\left(w\cdot w\right)-{\displaystyle {\sum }_{i=1}^N{\alpha }_i\left\{y_i\left[\left(w\cdot x_i\right)+b\right]-1\right\}}$ (12)

其中， $L\left(w,b,\alpha \right)$ 是拉格朗日泛函。

最优超平面问题的解在 $L\left(w,b,\alpha \right)$ 的鞍点上取得，满足对w和b的偏导数为零，通过求对偶问题的解可得：

$f\left(x\right)=\mathrm{sgn}\left\{g\left(x\right)\right\}=\mathrm{sgn}\left\{\left(w^{*}\cdot x\right)+b\right\}=\mathrm{sgn}\left\{{\displaystyle {\sum }_{i=1}^N{\alpha }_i^{\ast }{y}_i\left(x_i\cdot x\right)}+b^{*}\right\}$ (13)

其中， $w^{\ast }={\displaystyle {\sum }_{i=1}^N{\alpha }_i^{\ast }{y}_i{x}_i}$ 。

若样本集是非线性可分，就是说：

$y_i\left[\left(w\cdot x_i\right)+b\right]-1\ge 0,i=1,2,\cdots ,N$ (14)

式子(14)不可能被所有样本同时满足，因此引入松弛因子 ${\xi }_i$ 后约束条件变为：

$y_i\left[\left(w\cdot x_i\right)+b\right]-1+{\xi }_i\ge 0,i=1,2,\cdots ,N$ (15)

如果样本 $x_i$ 分类正确，则 ${\xi }_i=0$ ，否则 ${\xi }_i>0$ 。那么最优分类面的目标函数是：

$\underset{w,b}{\min }\frac{1}{2}\left(w\cdot w\right)+C\left({\displaystyle {\sum }_{i=1}^N{\xi }_i}\right)$ (16)

求解最优分类面的问题就转化为：

$\begin{array}{l}{\min }_{w,b,{\xi }_i}{\max }_{\alpha }L\left(w,b,\alpha \right)\\ =\frac{1}{2}\left(w\cdot w\right)+C{\displaystyle {\sum }_{i=1}^N{\xi }_i}-{\displaystyle {\sum }_{i=1}^N{\alpha }_i\left\{y_i\left[\left(w\cdot x_i\right)+b\right]-1+{\xi }_i\right\}}-{\displaystyle {\sum }_{i=1}^N{\gamma }_i{\xi }_i}\end{array}$ (17)

其中， ${\alpha }_i\ge 0$ ， ${\xi }_i\ge 0$ 是拉格朗日乘子，C是惩罚因子。

同样地，通过求对偶问题的解可得：

$f\left(x\right)=\mathrm{sgn}\left\{g\left(x\right)\right\}=\mathrm{sgn}\left\{\left(w^{*}\cdot x\right)+b\right\}=\mathrm{sgn}\left\{{\displaystyle {\sum }_{i=1}^N{\alpha }_i^{\ast }{y}_i\left(x_i\cdot x\right)}+b^{*}\right\}$ (18)

其中，这里的内积运算 $\left(x_i\cdot x\right)$ 等价于核函数 $K\left(x_i\cdot x_j\right)$ 。

常用的核函数有：

多项式核函数： $K\left(x,x^{\prime }\right)={\left(\left(x,x^{\prime }\right)+1\right)}^q$ ，采用这种核函数的SVM实现的是q阶的多项式判别函数。

径向基核函数： $K\left(x,x^{\prime }\right)=\exp \left(-\frac{{\Vert x-x^{\prime }\Vert }^2}{{\sigma }^2}\right)$ ，采用这种核函数的SVM实现的是与径向基网络形式相同的决策函数。

Sigmoid函数： $K\left(x,x^{\prime }\right)=\tanh \left(v\left(x\cdot x^{\prime }\right)+c\right)$ ，采用这种核函数的SVM实现的是在 和 满足一定取值条件下等价与包含一个隐层的多层感知机神经网络。

5. 仿真和算法过程

5.1. 在Yale Face Database上的实验

本实验使用YALE人脸库作为数据集，Yale Face Database是由10组图片，每组图片包含64张图片，一共640张图所组成的，大小是192像素 * 168像素。其中，图像的光照角度和强度有着不同程度的变化。我们将数据集中每组图的64张图，采取随机抽样，选取48张作为训练集，另外的16张作为测试集。所以，训练集一共有480张人脸图像样本，测试集一共有160张人脸图像样本。

5.2. 算法过程

5.2.1. 图像预处理

本文采用的预处理办法是LBP和直方图均衡。因为使用LBP和直方图均衡后，可以去除光照对灰度的影响，增强对比度以及锐化图像，使人脸的特征更加鲜明，提高人脸的辨识度。图6为原图和预处理后的图。使用圆形LBP算子，其中半径R为3，采样点数目为 $\text{3}*\text{8}=\text{24}$ 。

5.2.2. 栈式降噪自编码器提取人脸特征

经过SDA处理的训练集，先编码再解码，使得误差最小化，并且去除噪声对训练集的影响。实验使用3层的堆栈降噪自动编码机，第一层1024个神经元，第二层128个神经元，第三层16个神经元，这样每个人脸样本的特征向量由32,256维降到16维，那么这16维特征向量就可以代表该人脸的样本。

5.2.3. 构建多类SVM及核函数的选择

我们采用多类SVM分类器，用 $n=10$ 类样本构建 $\frac{n\left(n-1\right)}{2}$ 个分类器，核函数选择的是径向基核函数(RBF)，因此得到的支持向量机是一种径向基核函数分类器。

5.2.4. 实验结果

从表1中，我们可以明确得知，仅仅使用LBP模型对图片进行处理，识别的正确率只有57.1%；如果仅使用SDA模型对图片进行处理，识别的准确率也只有80.67%；如果使用LBP + PCA模型对图片进行处理，识别的准确率已经有87.6%；如果使用本文模型(LBP + SDA)对图片进行处理，识别的准确率高达92.56%。因此，通过与上述几种模型的对比，本文提出的LBP + SDA算法相对更优。

5.3. 实验分析

1) 用LBP算法，可以去除光照和角度的影响，增强了图像的特征，提高了识别率；

2) 使用SDA算法，可以快速降维，把特征向量从32,256维降到16维，这样提高了运算率和识别率。

Figure 5. Face contrast after preprocessing

图5. 预处理后的人脸对比

Table 1. Comparison of the recognition rate of the model

表1. 模型的识别率对比

6. 结论

本文结合LBP，SDA算法与SVM的特点，提出了基于SDA和LBP的人脸识别算法，并在YALE人脸库上做了仿真实验，结果表明提高了人脸的识别率，加快了运算的速率以及增强模型的鲁棒性。在进一步的学习过程中，我们可以在抖动，遮挡，分辨率等的影响下，探讨如何提高人脸的识别率。

基金项目

广州市科技计划资助项目(201707010435)。