亚纯函数及其差分乘积的零点分布

Meromorphic Function and Their Distribution of Zeros

摘要: 本文主要研究f(z) 为有限级超越亚纯函数时，差分乘积 的零点情况以及 的值分布情况，此处 ，c为任意非零常数满足 。

Abstract: In this paper, we study zeros of difference product and the value distribution of difference product under the condition of f(z) is a transcendental meromorphic function of finite order, where , c is a Non-zero constant such that .

1. 引言与定理

本文使用了Nevanlinna值分布论中常用记号及其基本结论 [1] 。本文出现的“亚纯函数”表示在整个复平面上亚纯。另外本文使用 $\sigma \left(f\right)$ 表示亚纯函数f的增长级，

$\lambda \left(f\right)$ 表示亚纯函数f的零点收敛指数， $\lambda \left(1/f\right)$ 表示亚纯函数f的极点收敛指数，记 $\Delta f\left(z\right)=f\left(z+c\right)-f\left(z\right)$，c为任意非零常数使得 $f\left(z+c\right)\cancel{\equiv }f\left(z\right)$ 。

Hayman在 [2] 中证明了下面定理。

定理A 若f为一个超越整函数且 $n\ge 2$，则 $f^n{f}^{\prime }$ 可取所有非零复常数无限多次。

2007年Laine和Yang在 [3] 中研究Hayman定理的差分形式的时候得出以下定理。

定理B 设 $f\left(z\right)$ 为有限级超越整函数，c为一非零复常数，则对于所有的 $n\ge 2$， $f^{n}f\left(z+c\right)$ 可取所有非零值a无限多次。

我们知道 $\Delta f\left(z\right)$ 能够看成 $f^{\prime }\left(z\right)$ 的差分形式，因此 $f^n\left(z\right)f^{\prime }\left(z\right)$ 的差分形式也可以看成 $f^n\left(z\right)\Delta f\left(z\right)$，因此 $f^n\left(z\right)\Delta f\left(z\right)$ 这一类差分乘积得到了数学家们的关注，其中Chen在 [4] 研究差分乘积 $f^n\left(z\right)\Delta f\left(z\right)$ 的零点情况时得到以下定理。

定理C 设 $f\left(z\right)$ 为有限级超越整函数，c为任意非零复常数使得 $f\left(z+c\right)\cancel{\equiv }f\left(z\right)$ 。

令 $H_n\left(z\right)=f^n\left(z\right)\Delta f\left(z\right)$， $n\ge 2$ 为整数。则以下结论成立

1) 若 $f\left(z\right)$ 具有无数多个零点，或者满足 $\sigma \left(f\right)\ne 1$，则 $H_n\left(z\right)$ 有无数多个零点。

2) 若 $f\left(z\right)$ 仅有有限多个零点并且满足 $\sigma \left(f\right)=1$，则 $H_n\left(z\right)$ 仅有有限多个零点。

本文将上述定理的“整函数”条件推广到“亚纯函数”，得到以下定理。

定理1 设 $f\left(z\right)$ 为极点收敛指数 $\lambda \left(1/f\right)<\sigma \left(f\right)<+\infty$ 的超越亚纯函数，c为任意非零复常数使得 $f\left(z+c\right)\cancel{\equiv }f\left(z\right)$ 。 $H_n\left(z\right)=f^n\left(z\right)\Delta f\left(z\right)$， $n\ge 2$ 为整数。则以下结论成立

1) 若 $f\left(z\right)$ 具有无数多个零点，或者满足 $\sigma \left(f\right)\ne 1$，则 $H_n\left(z\right)$ 有无数多个零点。

2) 若 $f\left(z\right)$ 仅有有限多个零点并且满足 $\sigma \left(f\right)=1$，则 $H_n\left(z\right)$ 仅有有限多个零点。

同时Chen在[4]中也考虑到差分乘积 $f{\left(z\right)}^n\Delta f\left(z\right)$ 当 $n=1$ 即 $f\left(z\right)\Delta f\left(z\right)$ 的值分布情况，并得到以下定理。

定理D $f\left(z\right)$ 为有限级超越整函数，且具有Borel例外值d，c为任意非零复常数使得 $f\left(z+c\right)\cancel{\equiv }f\left(z\right)$ 。函数集 $H\left(z\right)=f\left(z\right)\Delta f\left(z\right)$，则以下结论成立

1) $H\left(z\right)$ 可取任何非零复常数a无穷多次且满足 $\lambda \left(H-a\right)=\sigma \left(f\right)$ 。

2) 若 $d\ne 0$，则 $H\left(z\right)$ 无有限的Borel例外值。

3) 若 $d=0$，则0也是 $H\left(z\right)$ 的Borel例外值，从而 $H\left(z\right)$ 无有限非零的Borel例外值。

定理E $f\left(z\right)$ 为有限级超越整函数，c为任意非零复常数使得 $f\left(z+c\right)\cancel{\equiv }f\left(z\right)$ 。令 $H\left(z\right)=f\left(z\right)\Delta f\left(z\right)$，则以下结论成立

1) 若 $f\left(z\right)$ 仅有有限多个零点且满足 $\sigma \left(f\right)\ne 1$，或者 $f\left(z\right)$ 具有无穷多个零点，则 $H\left(z\right)$ 有无数多个零点。

2) 若 $f\left(z\right)$ 仅有有限多个零点并且满足 $\sigma \left(f\right)=1$，则 $H\left(z\right)$ 仅有有限多个零点。

本文将定理D、E中的整函数推广到亚纯函数得到如下定理。

定理2 设 $f\left(z\right)$ 为具有两个Borel例外值 $d,\infty$ 的有限级超越亚纯函数，c为任意非零复常数使得 $f\left(z+c\right)\cancel{\equiv }f\left(z\right)$ 。令 $H\left(z\right)=f\left(z\right)\Delta f\left(z\right)$，则以下结论成立

1) $H\left(z\right)$ 可取任何非零复常数a无穷多次且满足 $\lambda \left(H-a\right)=\sigma \left(f\right)$ 。

2) 若 $d\ne 0$，则 $H\left(z\right)$ 无有限的Borel例外值。

3) 若 $d=0$，则0也是 $H\left(z\right)$ 的Borel例外值，从而 $H\left(z\right)$ 无有限非零的Borel例外值。

定理3 设 $f\left(z\right)$ 为极点收敛指数 $\lambda \left(1/f\right)<\sigma \left(f\right)<+\infty$ 的超越亚纯函数，c为任意非零复常数使得 $f\left(z+c\right)\cancel{\equiv }f\left(z\right)$ 。令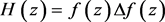，则以下结论成立

1) 若 $f\left(z\right)$ 仅有有限多个零点且满足 $\sigma \left(f\right)\ne 1$，或者 $f\left(z\right)$ 具有无穷多个零点，则 $H\left(z\right)$ 有无数多个零点。

2) 若 $f\left(z\right)$ 仅有有限多个零点并且满足 $\sigma \left(f\right)=1$，则 $H\left(z\right)$ 仅有有限多个零点。

最后，根据Borel例外值的定义，“ $f\left(z\right)$ 为具有两个Borel例外值 $d,\infty$ 的有限级超越亚纯函数”等价于 $\lambda \left(f\right)<\sigma \left(f\right)$， $$ 。

2. 引理

本文定理的证明需要用到下述引理。

引理1 [5] 设 $f\left(z\right)$ 为差分方程 $f^{n}P\left(z,f\right)=Q\left(z,f\right)$，的一个非常数有限级亚纯解，此处 $P\left(z,f\right),Q\left(z,f\right)$ 为f的差分多项式，其系数 $a_j\left(z\right)\left(j=1,\cdots ,s\right)$ 为亚纯函数，令 $\delta <1$，若关于f及其平移的差分多项式 $Q\left(z,f\right)$ 的次数至多是n，则有

$m\left(r,P\left(z,f\right)\right)=o\left(\frac{T\left(r+\left|c\right|,f\right)}{r^{\delta }}\right)+o\left(T\left(r,f\right)\right)+O\left({\displaystyle \underset{j=1}{\overset{s}{\sum }}m\left(r,a_j\right)}\right).$

对所有的r除去一个关于r的可能存在的具有有限对数测度的例外集成立。

引理2 [6] 设 $f_j\left(z\right)\left(j=1,\cdots ,n\right)\left(n\ge 2\right)$ 为亚纯函数， $g_j\left(z\right)\left(j=1,\cdots ,n\right)\left(n\ge 2\right)$ 为整函数且满足

1) ${\displaystyle {\sum }_{j=1}^n{f}_j\left(z\right){\text{e}}^{g_j\left(z\right)}}\equiv 0$ ；

2) 当 $1\le j<k\le n$ 时， $g_j\left(z\right)-g_k\left(z\right)$ 不是常数；

3) 当 $1\le j\le n,1\le h<k\le n$ 时， $T\left(r,f_j\right)=o\left\{T\left(r,{\text{e}}^{g_h-g_k}\right)\right\}\left(r\to \infty ,r\notin E\right)$， $E\subset \left(1,\infty \right)$ 为具有有限线性测度或有限对数测度的集合。则有 $f_j\left(z\right)\equiv 0\left(j=1,\cdots ,n\right)$ 。

引理3 [7] 设 $f\left(z\right)$ 为非常数有限级亚纯函数，对 $c\in C\backslash \left(0\right)$，有

$m\left(r,\frac{f\left(z+c\right)}{f\left(z\right)}\right)=S\left(r,f\right).$

引理4 [7] 设 $f\left(z\right)$ 为极点收敛指数 $\lambda \left(1/f\right)=\lambda <+\infty$ 的超越亚纯函数，c为任意非零复常数，则对 $\forall \epsilon >0$ 有

$N\left(r,f\left(z+c\right)\right)=N\left(r,f\right)+O\left(r^{\lambda -1+\epsilon }\right)+O\left(\log r\right).$

引理5 设 $f\left(z\right)$ 为极点收敛指数 $\lambda \left(1/f\right)<\sigma \left(f\right)<+\infty$ 的超越亚纯函数，c为任意非零复常数，令 $H_n\left(z\right)=f^n\left(z\right)\Delta f\left(z\right)\left(n\ge 1\right)$，则 $\sigma \left(H_n\right)=\sigma \left(f\right)$ 。

证明： $H_n\left(z\right)=f^n\left(z\right)\Delta f\left(z\right)=f{\left(z\right)}^{n+1}\frac{\Delta f\left(z\right)}{f\left(z\right)}.$ (2.1)

由(2.1)以及引理3、4可得

$m\left(r,H_n\right)\le \left(n+1\right)m\left(r,f\right)+m\left(r,\frac{\Delta f\left(z\right)}{f\left(z\right)}\right)=\left(n+1\right)m\left(r,f\right)+O\left(r^{\sigma -1+\epsilon }\right).$

$N\left(r,H_n\right)\le nN\left(r,f\right)+N\left(r,\Delta f\left(z\right)\right)\le \left(n+2\right)N\left(r,f\right)+O\left(r^{\lambda -1+\epsilon }\right)+O\left(\log r\right).$

于是

$T\left(r,H_n\right)\le \left(n+2\right)T\left(r,f\right)+O\left(r^{\sigma -1+\epsilon }\right)+O\left(\log r\right).$

这意味着 $\sigma \left(H_n\right)\le \sigma \left(f\right)$ 。接下来证明 $\sigma \left(H_n\right)\ge \sigma \left(f\right)$ 。

由(2.1)以及引理3、4也可得

$\left(n+1\right)m\left(r,f\right)=m\left(r,f^{n+1}\right)\le m\left(r,H_n\right)+m\left(r,\frac{f\left(z\right)}{\Delta f\left(z\right)}\right)=m\left(r,H_n\right)+O\left(r^{\sigma -1+\epsilon }\right).$

由 $\lambda \left(1/f\right)<\sigma \left(f\right)$ 得， $N\left(r,f\right)=O\left(r^{\sigma -1+\epsilon }\right)$ 。

因此 $T\left(r,f\right)\le m\left(r,H_n\right)+O\left(r^{\sigma -1+\epsilon }\right)$ 。从而， $\sigma \left(H_n\right)\ge \sigma \left(f\right)$ 结论成立。

3. 定理1的证明

证明：1) 因为 $f\left(z\right)$ 为超越亚纯函数且 $\Delta f\left(z\right)\cancel{\equiv }0$，从而当 $f\left(z\right)$ 有无穷多个零点时， $H_n\left(z\right)$ 具有无穷多个零点。

现假设 $f\left(z\right)$ 仅有有限多个零点且 $\sigma \left(f\right)\ne 1$ 。又因为 $f\left(z\right)$ 为超越亚纯函数，故 $f\left(z\right)$ 能写成以下形式

$f\left(z\right)=\frac{p_1\left(z\right)}{p_2\left(z\right)}{\text{e}}^{q\left(z\right)}:=r\left(z\right){\text{e}}^{q\left(z\right)}.$ (3.1)

此处 $q\left(z\right)$ 为多项式， $p_1\left(z\right)$ 为整函数满足 $\sigma \left(p_1\right)<\sigma \left(f\right)$， $p_2\left(z\right)$ 为 $f\left(z\right)$ 极点的典型乘积，因此 $\sigma \left(p_2\right)=\lambda \left(p_2\right)=\lambda \left(1/r\right)=\lambda \left(1/f\right)<\sigma \left(f\right)$ 。显然 $\sigma \left(r\right)<\sigma \left(f\right)$ 。

由(3.1)可得 $f\left(z+c\right)=r\left(z+c\right){\text{e}}^{q\left(z+c\right)}$ 。因此

$H_n\left(z\right)=r{\left(z\right)}^{n}r\left(z+c\right){\text{e}}^{nq\left(z\right)+q\left(z+c\right)}-r{\left(z\right)}^{n+1}{\text{e}}^{\left(n+1\right)q\left(z\right)}.$ (3.2)

由引理5及 $f\left(z\right)$ 为超越函数，可得 $H_n\left(z\right)$ 为超越函数，故 $H_n\left(z\right)$ 能表示成如下形式

$H_n\left(z\right)=\frac{g\left(z\right)}{p\left(z\right)}{\text{e}}^{q_1\left(z\right)}:=r_1\left(z\right){\text{e}}^{q_1\left(z\right)}.$ (3.3)

此处 $q_1\left(z\right)$ 为多项式， $g\left(z\right)$ 为整函数满足 $\sigma \left(g\right)<\sigma \left(H_n\right)$， $p\left(z\right)$ 为 $H_n\left(z\right)$ 极点的典型乘积，因此 $\sigma \left(p\right)=\lambda \left(p\right)=\lambda \left(1/r_1\right)=\lambda \left(1/H_n\right)<\sigma \left(H_n\right)$ 。显然 $\sigma \left(r_1\right)<\sigma \left(H_n\right)$ 。

由(3.2) (3.3)可得

$r{\left(z\right)}^{n}r\left(z+c\right){\text{e}}^{nq\left(z\right)+q\left(z+c\right)}-r{\left(z\right)}^{n+1}{\text{e}}^{\left(n+1\right)q\left(z\right)}=r_1\left(z\right){\text{e}}^{q_1\left(z\right)}.$ (3.4)

假设 $q\left(z\right)=a_k{z}^k+a_{k-1}{z}^{k-1}+\cdots +a_0,a_k\ne 0$，此处 $a_k,\cdots ,a_0$ 为常数，由 $\sigma \left(f\right)\ne 1$ 可知 $k\ge 2$ 。因此 $q\left(z+c\right)=a_k{z}^k+\left(kc{a}_k+a_{k-1}\right)z^{k-1}+{a^{\prime }}_{k-2}{z}^{k-2}+\cdots +{a^{\prime }}_0$，此处 ${a^{\prime }}_{k-2},\cdots ,{a^{\prime }}_0$ 为常数。

由 $a_k\ne 0$ 可知 $\left(n+1\right)a_{k-1}\ne kc{a}_k+\left(n+1\right)a_{k-1}$，故 $\left(n+1\right)q\left(z\right)-\left(nq\left(z\right)+q\left(z+c\right)\right)$ 不为常数。

若 $nq\left(z\right)+q\left(z+c\right)-q_1\left(z\right)$ 和 $\left(n+1\right)q\left(z\right)-q_1\left(z\right)$ 都不为常数，则由引理2及(3.4)可得 $r{\left(z\right)}^{n}r\left(z+c\right)\equiv 0,r{\left(z\right)}^{n+1}\equiv 0,r\left(z\right)\equiv 0$ 。这是矛盾的。

若 $nq\left(z\right)+q\left(z+c\right)-q_1\left(z\right)=b$，b为非零常数。即 $nq\left(z\right)+q\left(z+c\right)-b=q_1\left(z\right)$，因此(3.4)可变为

$\left[r{\left(z\right)}^{n}r\left(z+c\right)-{\text{e}}^{-b}{r}_1\left(z\right)\right]{\text{e}}^{nq\left(z\right)+q\left(z+c\right)}-r{\left(z\right)}^{n+1}{\text{e}}^{\left(n+1\right)q\left(z\right)}\text{=}0.$ (3.5)

由(3.5)及引理2可得 $r{\left(z\right)}^{n}r\left(z+c\right)-{\text{e}}^{-b}{r}_1\left(z\right)\equiv 0,r{\left(z\right)}^{n+1}\equiv 0$ 。这也是矛盾的。

若 $\left(n+1\right)q\left(z\right)-q_1\left(z\right)$ 为常数，则可由同样的方法得到矛盾。因此可得 $H_n\left(z\right)$ 有无穷多个零点。

2) 假设 $f\left(z\right)$ 仅有有限多个零点且 $\sigma \left(f\right)=1$ 。则 $$ 可写成如下形式

$f\left(z\right)=\frac{p_1^{\ast }\left(z\right)}{p_2^{\ast }\left(z\right)}{\text{e}}^{az+d}:=r^{\ast }\left(z\right){\text{e}}^{az+d}.$ (3.6)

此处 $$ 为常数， $p_1^{\ast }\left(z\right)$ 为多项式， $p_2^{\ast }\left(z\right)$ 为 $f\left(z\right)$ 极点的典型乘积，因此 $\sigma \left(p_2^{\ast }\right)=\lambda \left(p_2^{\ast }\right)=\lambda \left(1/r^{\ast }\right)=\lambda \left(1/f\right)<\sigma \left(f\right)$ 。显然 $\sigma \left(r^{\ast }\right)<\sigma \left(f\right)$ 。

由(3.6)可得

$f\left(z+c\right)=r^{\ast }\left(z+c\right){\text{e}}^{ac}{\text{e}}^{az+d},H_n\left(z\right)=\left\{r^{\ast }{\left(z\right)}^n\left(r^{\ast }\left(z+c\right){\text{e}}^{ac}-r^{\ast }\left(z\right)\right)\right\}{\text{e}}^{\left(n+1\right)\left(az+d\right)}.$

因为 $f\left(z+c\right)\cancel{\equiv }f\left(z\right)$，所以 $r^{\ast }\left(z+c\right){\text{e}}^{ac}-r^{\ast }\left(z\right)\cancel{\equiv }0$ 。又因为 $r^{\ast }\left(z\right)\cancel{\equiv }0$，故 $H_n\left(z\right)$ 仅有有限多个零点。

4. 定理2的证明

我们先证明第2)和3)。

2) 假设 $d\ne 0$，则 $f\left(z\right)$ 能写成如下形式。

$f\left(z\right)=d+\frac{p_1\left(z\right)}{p_2\left(z\right)}{\text{e}}^{a{z}^m}:=d+r\left(z\right){\text{e}}^{a{z}^m}.$ (4.1)

此处a为非零常数，m为正整数， $p_1\left(z\right)$ 为整函数满足 $\sigma \left(p_1\right)<\sigma \left(f\right)$， $p_2\left(z\right)$ 为 $f\left(z\right)$ 极点的典型乘积，因此 $\sigma \left(p_2\right)=\lambda \left(p_2\right)=\lambda \left(1/r\right)=\lambda \left(1/f\right)<\sigma \left(f\right)$ 。显然 $\sigma \left(r\right)<\sigma \left(f\right)$ 。因此

$f\left(z+c\right)=d+r\left(z+c\right)r^{\prime }\left(z\right){\text{e}}^{a{z}^m}.$ (4.2)

此处 $r^{\prime }\left(z\right)$ 为整函数，且满足 $\sigma \left(f\right)=m-1$ 。由(4.1) (4.2)得

$H\left(z\right)=r\left(z\right)\left[r\left(z+c\right)r^{\prime }\left(z\right)-r\left(z\right)\right]{\text{e}}^{2a{z}^m}+d\left[r\left(z+c\right)r^{\prime }\left(z\right)-r\left(z\right)\right]{\text{e}}^{a{z}^m}.$ (4.3)

由 $f\left(z+c\right)\cancel{\equiv }f\left(z\right)$，可得 $r\left(z+c\right)r^{\prime }\left(z\right)-r\left(z\right)\cancel{\equiv }0$ (4.4)

由(4.3) (4.4)可得 $H\left(z\right)$ 为有限级超越亚纯函数，且满足 $\sigma \left(H\right)=\sigma \left(f\right)=m$ 。

若 $H\left(z\right)$ 有Borel例外值 $d^{\ast }$，则 $H\left(z\right)$ 可表示成如下形式。

$H\left(z\right)=d^{\ast }+\frac{g\left(z\right)}{p\left(z\right)}{\text{e}}^{b{z}^m}:=d^{\ast }+r^{\ast }\left(z\right){\text{e}}^{b{z}^m}.$ (4.5)

此处b为非零常数，m为正整数， $g\left(z\right)$ 为整函数满足 $\sigma \left(g\right)<\sigma \left(H\right)$， $p\left(z\right)$ 为 $H\left(z\right)$ 极点的典型乘积，因此 $\sigma \left(p\right)=\lambda \left(p\right)=\lambda \left(1/r^{\ast }\right)=\lambda \left(1/H\right)<\sigma \left(H\right)$ 。 $\sigma \left(r^{\ast }\right)<\sigma \left(H\right)=m$ 。

由(4.3) (4.5)可得

$r\left(z\right)\left[r\left(z+c\right)r^{\prime }\left(z\right)-r\left(z\right)\right]{\text{e}}^{2a{z}^m}+d\left[r\left(z+c\right)r^{\prime }\left(z\right)-r\left(z\right)\right]{\text{e}}^{a{z}^m}-d^{\ast }-r^{\ast }\left(z\right){\text{e}}^{b{z}^m}=0.$ (4.6)

若 $b\ne a$ 且 $b\ne 2a$，则由引理2和(4.6)可得

$r\left(z+c\right)r^{\prime }\left(z\right)-r\left(z\right)\equiv 0,$

这是矛盾的。

若 $b=a$ 或 $b=2a$，则利用定理1中得出(3.5)式的方法也可以推出矛盾。因此， $H\left(z\right)$ 无有限的Borel例外值，(2)证明完毕。

下证(3)，若 $d=0$ 为 $f\left(z\right)$ 的Borel例外值，利用同样的方法由(4.3)可得

$H\left(z\right)=r\left(z\right)\left[r\left(z+c\right)r^{\prime }\left(z\right)-r\left(z\right)\right]{\text{e}}^{2a{z}^m}.$ (4.7)

因为 $r\left(z\right)\left[r\left(z+c\right)r^{\prime }\left(z\right)-r\left(z\right)\right]\cancel{\equiv }0$ 且 $\sigma \left(r\left(z\right)\left[r\left(z+c\right)r^{\prime }\left(z\right)-r\left(z\right)\right]\right)<m$，所以0为 $H\left(z\right)$ 的Borel例外值，从而 $H\left(z\right)$ 再无非零有限的Borel例外值。

最后证明1)，由2) 3)可知若 $f\left(z\right)$ 有有限的Borel例外值，则任何非零有限值a必不为 $H\left(z\right)$ 的Borel例外值。因此 $H\left(z\right)$ 可取a无穷多次，因此可得 $\lambda \left(H-a\right)=\sigma \left(H\right)=\sigma \left(f\right)$ 。

5. 定理3的证明

1) 因为 $f\left(z\right)$ 为亚纯函数且 $\Delta f\left(z\right)\cancel{\equiv }0$，所以当 $f\left(z\right)$ 有无穷多个零点时 $H\left(z\right)$ 也有无穷多个零点。

现假设 $f\left(z\right)$ 有有限多个零点且 $\sigma \left(f\right)\ne 1$，因此 $f\left(z\right)$ 能写成如下形式

$f\left(z\right)=\frac{p_1\left(z\right)}{p_2\left(z\right)}{\text{e}}^{h\left(z\right)}:=r\left(z\right){\text{e}}^{h\left(z\right)}.$ (5.1)

此处 $h\left(z\right)$ 为多项式， $\mathrm{deg}h\left(z\right)\ge 2$， $p_1\left(z\right)$ 为多项式， $p_2\left(z\right)$ 为 $f\left(z\right)$ 极点的典型乘积，因此 $\sigma \left(p_2\right)=\lambda \left(p_2\right)=\lambda \left(1/r\right)=\lambda \left(1/f\right)<\sigma \left(f\right)$ 。显然 $\sigma \left(r\right)<\sigma \left(f\right)$ 。

由(5.1)可得 $f\left(z+c\right)=r\left(z+c\right){\text{e}}^{h\left(z+c\right)}$ 。因此

$H\left(z\right)=r\left(z\right)r\left(z+c\right){\text{e}}^{h\left(z\right)+h\left(z+c\right)}-r{\left(z\right)}^2{\text{e}}^{2h\left(z\right)}.$ (5.2)

由引理5及 $f\left(z\right)$ 为超越函数，可得 $H\left(z\right)$ 为超越函数，故 $H\left(z\right)$ 能表示成如下形式

$H\left(z\right)=\frac{g\left(z\right)}{p\left(z\right)}{\text{e}}^{h^{\ast }\left(z\right)}:=r^{\ast }\left(z\right){\text{e}}^{h^{\ast }\left(z\right)}.$ (5.3)

此处 $h^{\ast }\left(z\right)$ 为多项式， $g\left(z\right)$ 为整函数满足 $\sigma \left(g\right)<\sigma \left(H\right)$， $p\left(z\right)$ 为 $H\left(z\right)$ 极点的典型乘积，因此 $\sigma \left(p\right)=\lambda \left(p\right)=\lambda \left(1/r^{\ast }\right)=\lambda \left(1/H\right)<\sigma \left(H\right)$ 。显然 $\sigma \left(r^{\ast }\right)<\sigma \left(H\right)$ 。

由(5.2) (5.3)可得

$r\left(z\right)r\left(z+c\right){\text{e}}^{h\left(z\right)+h\left(z+c\right)}-r{\left(z\right)}^2{\text{e}}^{2h\left(z\right)}=r^{\ast }\left(z\right){\text{e}}^{h^{\ast }\left(z\right)}.$ (5.4)

若 $h\left(z\right)+h\left(z+c\right)-h^{\ast }\left(z\right)$ 和 $2h\left(z\right)-h^{\ast }\left(z\right)$ 都不为常数，则由引理2及(5.4)可得 $r\left(z\right)r\left(z+c\right)\equiv 0$， $r{\left(z\right)}^2\equiv 0$， $r^{\ast }\left(z\right)\equiv 0$ 。这是矛盾的。

若 $h\left(z\right)+h\left(z+c\right)-h^{\ast }\left(z\right)$ 或 $2h\left(z\right)-h^{\ast }\left(z\right)$ 为常数，则用证明定理1的方法也可以得到矛盾结论。因此 $H\left(z\right)$ 有无穷多个零点。

2) 假设 $f\left(z\right)$ 仅有有限多个零点且 $\sigma \left(f\right)=1$ 。则用证明定理1中证明2)的方法也可以得出结论。因此定理3证明完毕。

基金项目

广东省自然科学基金资助项目(2016A030313002)，广东高校特色创新项目(2016KTSCX145)。