特征多项式理论在布尔控制网络中的应用

doi:10.12677/DSC.2018.73023

期刊菜单

特征多项式理论在布尔控制网络中的应用
The Application of Characteristic Polynomial Theory in Boolean Control Network

DOI: 10.12677/DSC.2018.73023, PDF, HTML, XML, 下载: 1,092 浏览: 2,231
作者: 郭向东, 陈芳跃：杭州电子科技大学，浙江杭州
关键词: 布尔控制网络；特征多项式方法；单节点扰动；布尔网络的同步；Boolean Control Network； Characteristic Polynomial Method； Single Node Perturbation； Synchronization of Boolean Networks

摘要: 首先，本文介绍了布尔控制网络的基本概念。然后，我们利用特征多项式方法研究布尔控制网络的动力学性质，包括极限环、吸引子与暂态，并以哺乳动物细胞周期调节网络为例进行说明。其次，本文利用一个布尔逻辑方程模拟网络演化过程中的状态突变，研究了单个节点扰动对布尔控制网络动力学性质的影响。接着，本文从特征多项式的角度研究了主从动布尔控制网络的动力学性质，得到其同步关系。该方法可以简便有效地得到布尔控制网络的动力学性质。

Abstract: First, this paper introduces the basic concepts of Boolean Control Networks. Second, we use the method of characteristic polynomial to study the dynamics of the Boolean Control Network, including limit cycles, attractors and transients, and use a mammalian cell cycle regulation network as an example. Next, this paper uses a Boolean logical expression to simulate the state mutation in the network evolution process, and studies the influence of individual node disturbance on the dynamics of the Boolean control network. Then, from the perspective of characteristic polynomials, this paper studies the dynamic properties of the master-slave Boolean control network and obtains its synchronization relationship. This method can easily and effectively get the dynamics of Boolean control network.

文章引用：郭向东, 陈芳跃. 特征多项式理论在布尔控制网络中的应用[J]. 动力系统与控制, 2018, 7(3): 214-225. https://doi.org/10.12677/DSC.2018.73023

1. 引言

1969年Kauffman首次提出了布尔网络 [1] 的概念，用来描述细胞与基因调控网络 [2] 。假设基因的表达只有表达和不表达两种状态，不同基因的调控关系用布尔函数来模拟，那么布尔网络就可以用来模拟基因调控网络。它既可以模拟许多网络控制中的非线性动力学行为，也能描述复杂网络的动态行为，所以布尔网络己成为研究基因调控网络以及细胞网络的重要模型。布尔网络是一种离散动力系统，其状态演化采用同步更新机制，并且某一布尔变量在t + 1时刻的状态由与某些布尔变量在t时刻的状态所决定，其状态演化过程具有一定的逻辑规则。某一时刻网络中由所有布尔变量的状态构成的向量称为系统的状态。这些变量一般分布在不同的吸引子区域或区域之外，区域外变量的状态定义为暂态。随着时间的演化，系统会从初始状态出发，按照特定的逻辑规则由暂态逐渐向吸引子演化。

布尔网络是一个逻辑演化的动力系统，具有复杂的动力学行为。逻辑准则和初始状态的不同以及扰动都可能改变布尔网络的动力学性质，使系统的状态在不同吸引子区域之间动态跃迁。Albert和Barabasi研究了布尔网络中的不动点，环及暂态问题 [3] [4] ，Akutsu研究了布尔网络的实现问题 [5] 。

近年来布尔控制网络正逐渐成为控制论领域的热点问题。有些不受自身或其他物质影响的物质，比如对生物学系统起到调控作用的药物，被描述为“控制”。这种包括控制的网络被称为布尔控制网络。由于控制理论的迅速发展，从控制理论的角度来研究布尔网络，可以更好地刻画其拓扑结构。程代展提出了矩阵的半张量积 [6] ，将布尔网络转化为逻辑系统的代数形式，逻辑方程可以用矩阵表达 [7] 。这种方法可以将布尔控制网络从逻辑动态系统转化为离散动力系统。目前，矩阵的半张量积已成为研究逻辑动态系统的重要工具之一，在布尔网络的分析与控制上已取得一系列具有突破意义的成果 [8] 。文献 [9] 给出了计算布尔网络不同长度极限环个数等拓扑性质的显式公式。另外，文献 [10] 提出了一种表征布尔网络拓扑结构的替代方法—特征多项式方法：根据给定的布尔网络的线性表达式，建立了其动力学与特征多项式之间的相关线性化矩阵，以此研究布尔网络的极限环、吸引子与暂态等动力学性质。文献 [11] 建立了布尔网络的线性化矩阵的特征多项式与非线性丢番图方程的对应关系，对布尔网络进行了动力学分类。因此，特征多项式方法是可行且有效的。本文利用特征多项方法 [10] 对几类布尔控制网络的动力学性质进行研究，计算出了布尔控制网络的极限环、吸引子及暂态个数，并用该方法研究了单节点扰动及布尔网络的同步问题，说明该方法是准确高效的。本文提出了一种描述布尔控制网络拓扑结构的新方法，对复杂控制网络的研究具有重要意义。

2. 布尔控制网络及其动力学性质

2.1. 布尔控制网络的基本概念

在布尔控制网络中，一个节点的状态可以用一个二元变量来描述，即“0”或“1”。不同节点之间的相互影响可以由布尔逻辑函数来描述。所以，布尔控制网络的动态方程 [11] 为：

(1.1)

其中 $x_{a} (t) \in P, a = 1, 2, \dots, m$ 是状态变量， $u_{b} (t) \in P, b = 1, 2, \dots, n$ 为控制变量， $f_{a}$ 为 $P^{m + n} \to P$ 的逻辑函数， $t = 0, 1, 2, \dots$ 是时间序列。

2.2. 布尔网络的特征多项式

1) 一个较复杂的N节点布尔控制网络的一般形式不方便储存和传输，可以用布尔矩阵对其进行描述(每行只有一个元素为“1”并且其余元素均为“0”的 $2^{N} \times 2^{N}$ -阶矩阵被称作布尔矩阵)。我们利用布尔网络线性化矩阵 [12] 的概念对布尔控制网络进行编码及线性化，得到相应的线性化矩阵，就称作该布尔控制网络对应的布尔矩阵。式(1.1)中的布尔控制网络对应一个 $(2^{m + n} \times 2^{m + n})$ -阶布尔矩阵B：

$B = [\begin{matrix} 1 & 2 & 3 & \dots & 2^{m + n} - 1 & 2^{m + n} \\ i_{1} & i_{2} & i_{3} & \dots & i_{2^{m + n} - 1} & i_{2^{m + n}} \end{matrix}] \begin{matrix} k \\ i_{k} \end{matrix}$ (1.2)

其中，i_k代表B的第k个行向量的第i_k个元素为1。矩阵中的元素(k,i_k)表示布尔控制网络的第k个节点下一时刻的状态为i_k。

2) 根据代数学的基本知识，任一个 $2 m + n$ -阶的布尔矩阵B存在一个非退化的矩阵W，使得 $\tilde{B} = W B W^{- 1}$ ，其中 $\tilde{B}$ 是如下形式 [13] ：

$\tilde{B} = (\begin{matrix} A_{0} & A_{1} & A_{2} & \dots & A_{n} \\ O & B_{i_{1}} & 0 & \dots & 0 \\ O & O & B_{i_{2}} & \dots & O \\ ⋮ & ⋮ & ⋮ & ⋱ & ⋮ \\ O & O & O & \dots & B_{i_{n}} \end{matrix})$ ， $B_{i_{j}} = (\begin{matrix} C_{j} & O & O & \dots & O \\ O & C_{j} & O & \dots & O \\ O & O & C_{j} & \dots & O \\ ⋮ & ⋮ & ⋮ & ⋱ & O \\ O & O & O & O & C_{j} \end{matrix})$

$C_{j} = (\begin{matrix} 0 & 1 & 0 & \dots & 0 \\ 0 & 0 & 1 & \dots & 0 \\ ⋮ & ⋮ & ⋮ & ⋱ & ⋮ \\ 0 & 0 & 0 & \dots & 1 \\ 1 & 0 & 0 & \dots & 0 \end{matrix})$ (1.3)

其中，A₀是 $s_{0} \times s_{0}$ 阶矩阵，A_j是 $s_{0} \times i_{j} s_{i_{j}}$ 阶矩阵 $(j = 1, 2, \dots, r)$ ，C_j是 $i_{j} \times i_{j}$ 阶矩阵 $(j = 1, 2, \dots, r)$ ， ${i_{1}, i_{2}, \dots, i_{r}} \subseteq {1, 2, \dots, 2^{n}}$ ， $i_{1} < i_{2} < \dots < i_{r}$ ， $s_{i_{j}} (j = 1, 2, \dots, r)$ 是正整数，并且有：

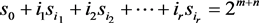(1.4)

在布尔矩阵B中，可以求得B的特征多项式：

$Φ (λ) = λ^{s_{0}} {(λ - 1)}^{s_{1}} {(λ^{2} - 1)}^{s_{2}} \dots {(λ^{i_{r}} - 1)}^{s_{i_{r}}}$ (1.5)

其中 $s_{0} \neq 2^{m + n}, s_{i} (i = 1, 2, \dots, 2^{m + n})$ 是非负整数。

3) 布尔控制网络的状态转移过程可以用有向图的拓扑结构 [13] 来描述，从而得到其环结构和暂态等动力学性质。一般地，周期环分为两类：一是吸引子，二是伊甸园孤岛。因此，我们可以利用线性化矩阵的特征多项式与动力学性质的关系，对布尔控制网络进行分析和研究。

2.3. 布尔网络的动力学性质与特征多项式的关系

定理 [14] 对任意一个布尔网络，其对应的布尔矩阵为B，B所对应的特征多项式为 $Φ (λ) = λ^{s_{0}} {(λ - 1)}^{s_{1}} {(λ^{2} - 1)}^{s_{2}} \dots {(λ^{i_{r}} - 1)}^{s_{i_{r}}}$ ，那么有：

1) 如果 $s_{0} = 0$ ，那么存在 $(s_{i_{1}} + s_{i_{2}} + \dots + s_{i_{r}})$ 个周期环，并且他们都是伊甸园孤岛，它们的周期分别是 $i_{j}$ ，并且满足，其中 $s_{i_{j}}$ 是 $i_{j}$ -周期环的数量；

2) 如果 $s_{0} \neq 0$ ，那么存在 $s_{0}$ 个暂态和 $(s_{i_{1}} + s_{i_{2}} + \dots + s_{i_{r}})$ 个周期环，并且这些周期环的周期分别是 $i_{j}$ ，进一步地满足 $s_{0} + i_{1} s_{i}_{_{1}} + i_{2} s_{i_{2}} + \dots + i_{r} s_{i_{r}} = 2^{m + n}$ ，其中 $s_{i_{j}}$ 是 $i_{j}$ -周期环的数量；另外，如果存在正整数 $q (1 \leq q \leq r)$ ，使得矩阵中的A_q是一个零矩阵，那么块矩阵 $B_{i_{j}}$ 所对应的 $i_{j}$ -周期环是伊甸园孤岛。

2.4. 系统稳定性与吸引盆的关系

系统稳定性是指系统在某些子系统行为失调时恢复到原来状态的能力或性质。布尔网络的动力学性质模型不依赖于参数，因此可以定性描述布尔控制网络的系统稳定性。

通向吸引子的状态集称为吸引子盆 [15] ，并且吸引子盆内的各种状态最终都通向吸引子的状态集。吸引子盆能使系统经过适当干扰后仍重复原来的状态循环，所以吸引子可以保持系统的稳定性。在布尔控制网络中，变量经过局部的突变重复原来的状态循环，就称该状态稳定。如果一个布尔控制网络受到干扰后恢复到原来状态的能力越强，系统稳定性就越高，反之系统稳定性越低。另外，吸引盆区域越大说明吸引子的影响力也越大，从而系统的稳定性就越强。

2.5. 哺乳动物细胞周期调节网络

考虑一个布尔控制网络：哺乳动物细胞周期调节的核心网络 [16] 。该网络包含一个输入CycD和九个状态(蛋白质Rb，E2，CycE，CycA，p27，Cdc20，Cdh1，UbcH10和CycB)，依次取u，x₁，x₂，x₃，x₄，x₅，x₆，x₇，x₈，和x₉，分别表示这十个变量激活(activation)与抑制(inactivation)两个状态，得到相应的布尔逻辑方程：

${\begin{cases} x_{1} (t + 1) = [u (t) \cap {\bar{x}}_{3} (t) \cap {\bar{x}}_{4} (t) \cap {\bar{x}}_{9} (t)] \cup [{\bar{x}}_{5} (t) \cap \bar{u} (t) \cap {\bar{x}}_{9} (t)] \\ x_{2} (t + 1) = [{\bar{x}}_{1} (t) \cap {\bar{x}}_{4} (t) \cap {\bar{x}}_{9} (t)] \cup [{\bar{x}}_{5} (t) \cap x_{1} (t) \cap {\bar{x}}_{9} (t)] \\ x_{3} (t + 1) = x_{2} (t) \cap {\bar{x}}_{1} (t) \\ x_{4} (t + 1) = [(x_{2} (t) \cap {\bar{x}}_{1} (t)) \cap {\bar{x}}_{6} (t) \cap \bar{[x_{7} (t) \cap x_{8} (t)]}] \\ \cup [(x_{4} (t) \cap {\bar{x}}_{1} (t)) \cap {\bar{x}}_{6} (t) \cap \bar{(x_{7} (t) \cap x_{8} (t))}] \\ x_{5} (t + 1) = [u (t) \cap {\bar{x}}_{3} (t) \cap {\bar{x}}_{4} (t) \cap {\bar{x}}_{9} (t)] \\ \cup [x_{5} (t) \cap \bar{(x_{3} (t) \cap x_{4} (t))} \cap \bar{u} (t) \cap {\bar{x}}_{9} (t)] \\ x_{6} (t + 1) = x_{9} (t) \\ x_{7} (t + 1) = [{\bar{x}}_{4} (t) \cap {\bar{x}}_{9} (t)] \cup x_{6} (t) \cup [x_{5} (t) \cap {\bar{x}}_{9} (t)] \\ x_{8} (t + 1) = {\bar{x}}_{7} (t) \cup [x_{7} (t) \cap x_{8} (t) \cap (x_{6} (t) \cap x_{4} (t) \cap x_{9} (t))] \\ x_{9} (t + 1) = {\bar{x}}_{6} (t) \cap {\bar{x}}_{7} (t) \end{cases}$ (1.6)

该网络对应的布尔矩阵(部分矩阵)如下：

$[\begin{matrix} 1 & 2 & 3 & 4 & \dots & 1021 & 1022 & 1023 & 1024 \\ 408 & 136 & 12 & 12 & \dots & 263 & 7 & 15 & 15 \end{matrix}] \begin{matrix} k \\ i_{k} \end{matrix}$ (1.7)

所对应布尔矩阵的特征多项式为：

$Φ (λ) = λ^{1020} (λ^{4} - 1)$ (1.8)

可以得到，该布尔控制网络共有1024个状态，只有1个吸引盆，其中1020个暂态，一个4-周期环。该细胞周期调节网络有1020个状态都收敛到44，9，405，199共四个吸引子上。该吸引盆覆盖网络的全部区域，表明该网络稳定程度很高。该网络对应的有向拓扑图(部分)如图1所示。

在该网络中，Rb，E2F，CycE，CycA，p27，Cdc20，Cdh1，UbcH10和CycB九个蛋白质可以组成512个状态。由于输入CycD的控制作用，当输入CycD为0或1时，这512个状态分别对应两种状态转移结果，两种结果可能相同，也可能不同。我们发现当输入CycD从0切换到1时，该调控网络277，279，280，405，407，408，437，440，469，471，501，504这12种状态都降低了272，分别对应5，7，8，133，135，136，165，168，197，199，229，232；这12种状态总共包含128个状态节点。输入CycD从0切换到1时，该调控网络261，263，26，389，391，421，424，453，455，485，488这11种状态都降低了256，分别对应5，7，8，133，135，165，168，197，199，229，232；这11种状态共包含32个状态节点。另外，有352个状态不受输入CycD的影响。可以得到，输入CycD能有规律地控制部分节点的状态转移方式，从而对该网络进行控制。这种情况对于哺乳动物细胞周期调节网络的稳定性来说是有利的，可以保证细胞周期调节功能的稳定性。另外，如果布尔控制逻辑方程中只有某一节点变化，会导致吸引子和周期环会发生较大变化，该网络将会出现新的动力学关系，吸引喷也会呈现新的控制区域。例如，将方程(1.3)中 $x_{1} (t + 1)$ 进行如下变化(将 $u (t)$ 与 ${\bar{x}}_{3} (t)$ 之间的关系由逻辑“并”变为逻辑“或”)：

$x_{1} (t + 1) = [u (t) | {\bar{x}}_{3} (t) \cap {\bar{x}}_{4} (t) \cap {\bar{x}}_{9} (t)] \cup [{\bar{x}}_{5} (t) \cap \bar{u} (t) \cap {\bar{x}}_{9} (t)]$ (1.9)

所对应布尔矩阵的特征多项式为 $Φ (λ) = λ^{1015} (λ^{9} - 1)$ ，形成1015个暂态和一个9-周期环。这说明细

胞周期调节网络某一部分发生变异很容易引起细胞周期调解网络的动力学关系。网络内部结构的改变容易引起内部秩序发生变化，从而引发变异。因此，该细胞周期调节网络是稳定的，但是内部结构的细微变化很可能引起整个网络结构的变化，这不利于该哺乳动物细胞的稳定性。不过，在某种程度上，它容易扩大局部变异的影响，再通过自然选择而发生进化。

Figure 1. The state transition diagram of the cycle regulatory network in mammalian cells

图1. 哺乳动物细胞周期调节网络状态转移图

3. 布尔控制网络的扰动

3.1. 单个节点扰动的布尔控制网络

在真实世界里，网络内部中子系统之间关系的突变、环境的瞬间改变容易使网络的演化过程在某些时刻发生状态突变。本文只考虑单个节点的状态发生扰动的情形，并利用另一个布尔控制网络对扰动进行模拟，从而分析新生成网络的动力学性质及稳定性。单个节点发生扰动的布尔逻辑方程：

${\begin{cases} x_{1} (t + 1) = g_{1} (x_{1} (t), x_{2} (t), \dots, x_{m} (t), u_{1} (t), u_{2} (t), \dots, u_{n} (t)) \\ x_{2} (t + 1) = g_{2} (x_{1} (t), x_{2} (t), \dots, x_{m} (t), u_{1} (t), u_{2} (t), \dots, u_{n} (t)) \\ ⋮ \\ x_{m} (t + 1) = g_{m} (x_{1} (t), x_{2} (t), \dots, x_{m} (t), u_{1} (t), u_{2} (t), \dots, u_{n} (t)) \end{cases}$ (2.1)

3.2. 两个例子

例1：布尔控制网络I

布尔控制网络逻辑方程：

${\begin{cases} x_{1} (t + 1) = x_{2} (t) \\ x_{2} (t + 1) = x_{3} (t) \\ x_{3} (t + 1) = u (t) \cup [x_{2} (t) \cap x_{3} (t)] \end{cases}$ (2.2)

扰动布尔逻辑方程：

${\begin{cases} x_{1} (t + 1) = {\bar{x}}_{2} (t) \\ x_{2} (t + 1) = {\bar{x}}_{3} (t) \\ x_{3} (t + 1) = x_{1} (t) \cap x_{3} (t) \end{cases}$ (2.3)

1) 若不考虑节点扰动的影响，该布尔控制网络对应的布尔矩阵：

$[\begin{matrix} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16 \\ 1 & 2 & 3 & 4 & 5 & 6 & 8 & 8 & 1 & 2 & 3 & 4 & 5 & 6 & 8 & 8 \end{matrix}] \begin{matrix} k \\ i_{k} \end{matrix}$ (2.4)

其所对应布尔矩阵的特征多项式为：

$Φ (λ) = λ^{9} {(λ - 1)}^{7}$ (2.5)

可以得到，该布尔控制网络有7个不动点和9个暂态。该网络对应的有向拓扑图如图2所示。

2) 若对16个节点k分别进行扰动，得到结果如表1所示。

在该布尔控制网络中，对于任一节点扰动所对应布尔矩阵的特征值都为1，对应特征多项式的形式为：

$Φ (λ) = λ^{16 - n} {(λ - 1)}^{n}, n = 6, 7$ (2.6)

不过，不同节点扰动对应的布尔矩阵不一定相同。

例2：布尔控制网络II

布尔控制网络逻辑方程：

${\begin{cases} x_{1} (t + 1) = [x_{2} (t) \cap x_{3} (t)] \leftrightarrow x_{5} (t) \\ x_{2} (t + 1) = [{\bar{x}}_{1} (t)] \cup x_{3} (t) \\ x_{3} (t + 1)) = {\bar{x}}_{4} (t) \\ x_{4} (t + 1) = [x_{1} (t) \cap x_{2} (t)] \cup x_{3} (t) \\ x_{5} (t + 1) = x_{1} (t) \leftrightarrow [x_{3} (t) \cup x_{4} (t)] \end{cases}$ (2.7)

Figure 2. The state transition diagram of nodeless disturbance of Boolean control network I

图2. 布尔控制网络I无节点扰动的状态转移图

Table 1. Number of Attractors with Different Perturbations in Boolean Control Network I

表1. 布尔控制网络I不同扰动的吸引子数量

扰动布尔逻辑方程：

${\begin{cases} x_{1} (t + 1) = {\bar{x}}_{2} (t) \cap x_{5} (t) \\ x_{2} (t + 1) = {\bar{x}}_{2} (t) \cap [x_{2} (t) \cup x_{3} (t)] \\ x_{3} (t + 1) = {\bar{x}}_{2} (t) \cap u (t) \cap [x_{1} (t) \cup x_{4} (t)] \\ x_{4} (t + 1) = {\bar{x}}_{2} (t) \cap u (t) \cap x_{1} (t) \\ x_{5} (t + 1) = {\bar{x}}_{2} (t) \cap {\bar{x}}_{3} (t) \end{cases}$ (2.8)

1) 若不考虑节点扰动的影响，该布尔控制网络对应的布尔矩阵(部分矩阵)：

$[\begin{matrix} 1 & 2 & 3 & 4 & \dots & 61 & 62 & 63 & 64 \\ 30 & 30 & 14 & 14 & \dots & 11 & 11 & 27 & 27 \end{matrix}] \begin{matrix} k \\ i_{k} \end{matrix}$ (2.9)

该网络对应的有向拓扑图(部分)如图3所示。

其所对应布尔矩阵的特征多项式为：

$Φ (λ) = λ^{62} (λ^{2} - 1)$ (2.10)

可以得到，该布尔控制网络有一个2-周期环和62个暂态。若对64个节点k分别进行扰动，得到结果如表2所示。

每一节点扰动对应布尔矩阵的特征多项式如表3所示。

3.3. 单个节点扰动的稳定性

上述两个例子说明不同节点的扰动所对应的布尔控制网络特征多项式有较大差异，并且改变了原网络的动力学性质，系统的稳定性也随之发生变化。在例2.2中，节点6的扰动使原网络产生了一个2-周期环和一个不动点；对节点15进行扰动，产生了一个2-周期环和一个3-周期环，出现了两个吸引盆；两

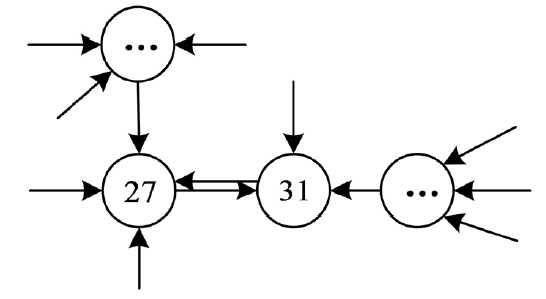
Figure 3. The state transition diagram of nodeless disturbance of Boolean control network II

图3. 布尔控制网络II无节点扰动的状态转移图

Table 2. Number of Attractors with Different Perturbations in Boolean Control Network II

表2. 布尔控制网络II不同扰动的吸引子数量

Table 3. Different perturbation characteristic polynomials of Boolean Control Network II

表3. 布尔控制网络II的不同扰动的特征多项式

注：若特征多项式相同，对应的布尔矩阵不一定相同。

者所对应布尔控制网络的系统稳定性都发生了较大变化。因此，在布尔控制网络中，单个节点发生扰动将对网络的演化方式有较大影响，从而影响对应布尔控制网络的动力学性质，改变系统的稳定性。

4. 布尔网络的同步

4.1. 布尔网络同步的基本概念

若性质全同或相近的两个或多个动力系统从不同的初始条件出发，因系统间的相互作用使动力系统各自的演化状态逐步接近，并且最终演化到全同的状态，那么就称这些动力系统同步。在两个确定布尔网络的同步问题中，产生命令的布尔网络称作主动布尔网络；带有控制输入及通过状态反馈 [17] 接收命令的布尔网络称作从动布尔网络 [18] 。

主动布尔网络动态方程：

${\begin{cases} x_{1} (t + 1) = f_{1} (x_{1} (t), x_{2} (t), \dots, x_{m} (t)) \\ x_{2} (t + 1) = f_{2} (x_{1} (t), x_{2} (t), \dots, x_{m} (t)) \\ ⋮ \\ x_{m} (t + 1) = f_{m} (x_{1} (t), x_{2} (t), \dots, x_{m} (t)) \end{cases}$ (2.11)

其中 $x_{a} (t) \in P (a = 1, 2, \dots, m)$ 是状态变量， $f_{a} : P^{m} \to P (a = 1, 2, \dots, m)$ 为逻辑函数， $t = 0, 1, 2, \dots$ 是时间序列。

从动布尔网络的动态方程：

${\begin{cases} s_{1} (t + 1) = g_{1} (s_{1} (t), s_{2} (t), \dots, s_{m} (t), u_{1} (t), u_{2} (t), \dots, u_{n} (t)) \\ s_{2} (t + 1) = g_{2} (s_{1} (t), s_{2} (t), \dots, s_{m} (t), u_{1} (t), u_{2} (t), \dots, u_{n} (t)) \\ ⋮ \\ s_{m} (t + 1) = g_{m} (s_{1} (t), s_{2} (t), \dots, s_{m} (t), u_{1} (t), u_{2} (t), \dots, u_{n} (t)) \end{cases}$ (2.12)

$s_{a} (t) \in P (a = 1, 2, \dots, m)$ 是状态变量， $u_{b} (t) \in P (b = 1, 2, \dots, n)$ 是控制变量， $g_{a} : P^{m + n} \to P (a = 1, 2, \dots, m)$ 为逻辑函数， $t = 0, 1, 2, \dots$ 是时间序列。

状态反馈控制的动态方程为：

${\begin{cases} u_{1} (t) = h_{1} (x_{1} (t), x_{2} (t), \dots, x_{m} (t), s_{1} (t), s_{2} (t), \dots, s_{m} (t)) \\ u_{2} (t) = h_{2} (x_{1} (t), x_{2} (t), \dots, x_{m} (t), s_{1} (t), s_{2} (t), \dots, s_{m} (t)) \\ ⋮ \\ u_{m} (t) = h_{m} (x_{1} (t), x_{2} (t), \dots, x_{m} (t), s_{1} (t), s_{2} (t), \dots, s_{m} (t)) \end{cases}$ (2.13)

$h_{a} : P^{2 m} \to P (a = 1, 2, \dots, m)$ 为逻辑函数， $t = 0, 1, 2, \dots$ 是时间序列。

4.2. 无状态反馈布尔网络的同步

例1：考虑下面两个布尔网络，其中布尔网络(2.14)称为主动布尔网络I，布尔网络(2.15)称为从动布尔网络I。

${\begin{cases} x_{1} (t + 1) = x_{2} (t) \cap x_{3} (t) \\ x_{2} (t + 1) = x_{1} (t) \cap {\bar{x}}_{2} (t) \end{cases}$ (2.14)

${\begin{cases} s_{1} (t + 1) = s_{1} (t) \bar{\cup} s_{2} (t) \cap u_{1} (t) \\ s_{2} (t + 1) = s_{1} (t) \bar{\cup} u_{2} (t) \end{cases}$ (2.15)

主动布尔网络对应的布尔矩阵：

$[\begin{matrix} 1 & 2 & 3 & 4 \\ 2 & 1 & 2 & 4 \end{matrix}] \begin{matrix} k \\ i_{k} \end{matrix}$ (2.16)

对应的有向拓扑图如图4所示。

对应布尔矩阵的特征多项式为：

$Φ (λ) = λ (λ^{2} - 1) (λ - 1)$ (2.17)

主动布尔网络有一个暂态、一个不动点和一个2-周期环。

从动布尔网络对应的布尔矩阵：

$[\begin{matrix} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16 \\ 2 & 1 & 2 & 1 & 2 & 1 & 4 & 3 & 1 & 2 & 3 & 4 & 1 & 2 & 1 & 2 \end{matrix}] \begin{matrix} k \\ i_{k} \end{matrix}$ (2.18)

对应的有向拓扑图如图5所示。

所对应布尔矩阵的特征多项式为：

$Φ (λ) = λ^{14} (λ^{2} - 1)$ (2.19)

可以得到，该布尔控制网络有一个2-周期环和14个暂态，主从动布尔网络对应的布尔矩阵中有三个相同的元素：节点1、节点2和节点3。主从布尔网络都包含由节点1和节点2构成的2-周期环。所以该主从动布尔网络实现了部分同步。

4.3. 含状态反馈布尔网络的同步

例2：再考虑下面两个布尔网络，其中布尔网络(2.20)称为主动布尔网络II，布尔网络(2.21)称为从动布尔网络II。

${\begin{cases} x_{1} (t + 1) = x_{2} (t) \cap x_{3} (t) \\ x_{2} (t + 1) = {\bar{x}}_{1} (t) \\ x_{3} (t + 1) = x_{2} (t) \cup x_{3} (t) \end{cases}$ (2.20)

${\begin{cases} s_{1} (t + 1) = s_{2} (t) \cap s_{3} (t) \\ s_{2} (t + 1) = {\bar{s}}_{1} (t) \cup u (t) \\ s_{3} (t + 1) = s_{2} (t) \cup s_{3} (t) \end{cases}$ (2.21)

Figure 4. The state transition diagram of Master Boolean Network I

图4. 主动布尔网络I的状态转移图

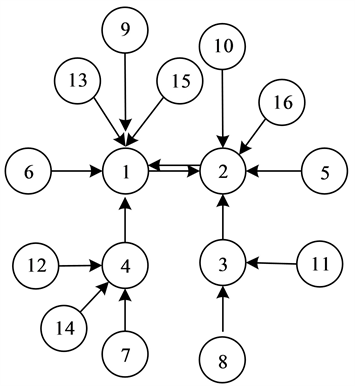
Figure 5. The state transition diagram of Slave Boolean Network I

图5. 从动布尔网络I的状态转移图

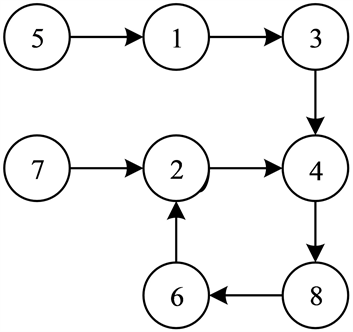
Figure 6. The state transition diagram of Boolean Network II

图6. 布尔网络II的状态转移图

状态反馈控制： $u (t) = [x_{1} (t) \bar{\cup} s_{1} (t)] \cup [x_{2} (t) \bar{\cup} s_{2} (t)]$

主动布尔网络II对应的布尔矩阵：

$[\begin{matrix} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ 3 & 4 & 4 & 8 & 1 & 2 & 2 & 6 \end{matrix}] \begin{matrix} k \\ i_{k} \end{matrix}$ (2.22)

所对应布尔矩阵的特征多项式为：

(2.23)

从动布尔网络II对应的布尔矩阵：

$[\begin{matrix} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ 3 & 4 & 4 & 8 & 1 & 2 & 2 & 6 \end{matrix}] \begin{matrix} k \\ i_{k} \end{matrix}$ (2.24)

所对应布尔矩阵的特征多项式为：

$Φ (λ) = λ^{4} (λ^{4} - 1)$ (2.25)

可以得到，主动布尔网络II和从动布尔控制网络II都有四个暂态和一个4-周期环。主从动布尔网络的布尔简化矩阵完全相同，其有向拓扑图也完全相同，如图6所示。即，二者有相同的动力学行为，实现完全同步。

5. 结论

本文利用特征多项式方法对布尔控制网络的动力学性质进行研究，得到了单个节点扰动对布尔控制网络动力学行为的影响，并且用该方法分析了主从动布尔网络的同步关系。从计算结果来看，特征多项式方法可以准确描述布尔控制网络的动力学行为，为布尔控制网络的研究提供了一定的参考。含较多节点的布尔控制网络需要通过更有效的算法来降低计算复杂度。

参考文献

[1]	Waldrop, M.M., 著. 复杂[M]. 陈玲, 译. 北京: 三联书店, 1997.
[2]	Kauffman, S.A. (1969) Metabolic Stability and Epigenesis in Randomly Constructed Genetic Nets. Journal of Theoretical Biology, 22, 437-467. https://doi.org/10.1016/0022-5193(69)90015-0
[3]	Albert, R. and Barabasi, A. (2000) Dynamics of Complex Systems: Scaling Laws for the Period of Boolean Networks. Physical Review Letters, 84, 5660-5663. https://doi.org/10.1103/PhysRevLett.84.5660
[4]	Aldana, M. (2003) Boolean Dynamics of Networks with Scale-Free Topology. Physica D: Nonlinear Phenomena, 185, 45-66. https://doi.org/10.1016/S0167-2789(03)00174-X
[5]	Akutsu, T., Hayashida, M., Ching, W.K., et al. (2007) Control of Boolean Networks: Hardness Results and Algorithms for Tree Structured Networks. Journal of Theoretical Biology, 244, 670-679. https://doi.org/10.1016/j.jtbi.2006.09.023
[6]	程代展, 齐洪胜, 矩阵的半张量积: 理论与应用[M]. 北京: 科学出版社, 2007.
[7]	Cheng, D.Z. and Qi, H.S. (2005) Matrix Expression of Logic and Fuzzy Control. Proceedings of the 44th IEEE Conference on Decision and Control, Seville, 15 December 2005, 3273-3278. https://doi.org/10.1109/CDC.2005.1582666
[8]	卢剑权, 李海涛, 刘洋, 等. 矩阵半张量积方法在逻辑网络和相关系统中的应用综述[J]. 南京信息工程大学学报, 2017, 9(4): 347-364.
[9]	Cheng, D.Z. and Qi, H.S. (2010) A Linear Representation of Dynamics of Boolean Networks. IEEE Transactions on Automatic Control, 55, 2251-2258. https://doi.org/10.1109/TAC.2010.2043294
[10]	He, Q.B., Chen, F.Y. and Liu, Z.R. (2010) Boolean Networks: Coding, Linearizing and Dynamics. International Workshop on Chaos-Fractal Theory and its Application, Kunming, 29-31 October 2010, 216-220.
[11]	Chen, F., Zhao, G., He, Q. and Jin, W. (2014) Dynamics Classification of Boolean Networks and Solutions of Diophantine Equation. Theoretical Mathematics and Applications, 4, 109-126.
[12]	Cheng, D., Qi, H. and Li, Z. (2011) Analysis and Control of Boolean Networks: A Semi-Tensor Product Approach. Spring-er-Verlag, New York. https://doi.org/10.1007/978-0-85729-097-7
[13]	Chua, L.O., Guan, J., Sbitnev, V.I. and Jinwook, S. (2007) A Nonlinear Dynamics Perspective of Wolfram’s New Kind of Science. Part VII: Isles of Eden. International Journal of Bifurcation and Chaos, 17, 2839-3012. https://doi.org/10.1142/S0218127407019068
[14]	Chen, F., Jin, W. and Wang, G. (2017) Characteristic Poly-nomial Method for Analyzing Dynamics of Boolean Networks. PHYSCON 2017.
[15]	李谋勋. 复杂系统布尔网络模型及应用[J]. 系统科学学报, 2006, 14(4): 35.
[16]	Faure, A., Naldi, A., Chaouiya, C., et al. (2006) Dynamical Anal-ysis of a Generic Boolean Model for the Control of the Mammalian Cell Cycle. Bioinformatics, 22, 124-131. https://doi.org/10.1093/bioinformatics/btl210
[17]	Li, R. and Chu, T. (2012) Complete Synchronization of Boolean Networks. IEEE Transactions on Neural Network and Learning Systems, 23, 840-846. https://doi.org/10.1109/TNNLS.2012.2190094
[18]	陈红委. 布尔网络的控制理论相关问题研究[D]: [硕士学位论文]. 金华: 浙江师范大学, 2014.

为你推荐

友情链接