1. 引言
常微分方程是数学中的一门重要学科。对于平面系统,我们在分析它的结构时首先要求解出奇点,对于奇点的类型大致分为以下几类:结点、焦点、中心、鞍点、高阶奇点等等。众所周知,奇点的线性化系数矩阵的特征值在奇点的初等分类中起着关键的作用。在有零特征值、纯虚数特征值和全零特征值的情况下有许多判断奇点的类型及稳定性的方法,本文对一类二次系统(II)类方程的奇点性态进行了分析。关于平面二次系统,有下述叶彦谦分类:
(I)类方程:
。
(II)类方程:
。
(III)类方程:
。
对于上述三类方程,当
时,以
为粗焦点,
时O为稳定,
时O为不稳定。
时,O为细焦点。
2. 预备知识
考虑平面二次系统
(2.1)
首先给出关于周期函数积分的一个引理。
引理1 ( [1] ):设
是以l为周期的连续周期函数,则
(2.2)
其中
仍以l为周期,
。
引理2 ( [2] ):设系统(2.1)右端解析,以
为平衡点,如果存在
的一个邻域U和U上的一个连续、可微函数
,且满足
1) F正定:
;
,当
。
2)
,当
。
则系统(2.1)的平衡点
渐近稳定(不稳定)。
引理3 ( [1] ):关于焦点量叶彦谦给出了如下公式:
有如下结论:
1) 当
,
,则点
为一阶细焦点,
时点
为稳定,
时点
为不稳定;
2) 当
,
,则点
为二阶细焦点,
时点
为稳定,
时点
为不稳定;
3) 当
,
,则点
为三阶细焦点,
时点
为稳定,
时点
为不稳定;
4) 当
时,点
为中心。
3. 主要结果
本文考虑了一类二次系统(II)类方程在奇点的性态。
当
,
,
时,(II)类方程化为
,
。
解:令
,
。得到下列4个奇点,分别为
1) 由于
是对应线性系统的中心,对其非线性系统在原点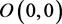 的性态分析,本文给出三种不同的方法判断原系统在原点
的性态分析,本文给出三种不同的方法判断原系统在原点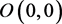 的性态,对于在点
的性态,对于在点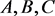 处的奇点性态,要作一线性变换,把它先移到原点进而再判断其稳定性态。
处的奇点性态,要作一线性变换,把它先移到原点进而再判断其稳定性态。
方法一(后继函数法):令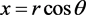 ,
, 。易计算得
。易计算得
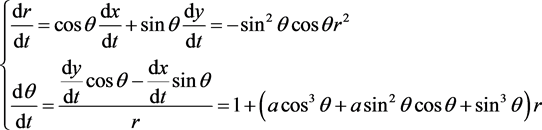
消去dt,利用泰勒公式展开,得到

对充分小的c,求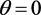 时
时 的解
的解

其中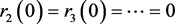 ,将
,将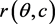 代入上述方程,比较c的同次幂系数,得
代入上述方程,比较c的同次幂系数,得
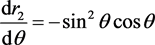


解得
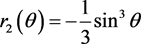
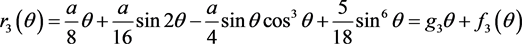
故而可知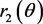 为周期函数,由引理1知
为周期函数,由引理1知 不是周期函数,其中
不是周期函数,其中 是周期函数,而
是周期函数,而
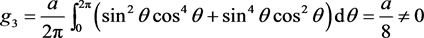 ,至此便可判定原点为原系统的一阶细焦点,当
,至此便可判定原点为原系统的一阶细焦点,当 时为不稳定,
时为不稳定, 时为稳定。
时为稳定。
方法二(形式级数判别法):假设原系统具有下列级数形式的解
令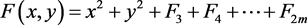
则
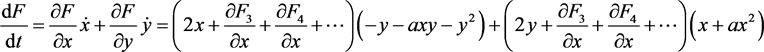
令三次项为0,则

取极坐标,令

上述化为

消去 ,得
,得
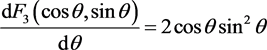
因为
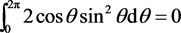
故
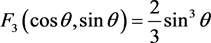
所以对应的三次齐次函数为

四次项显然为0,则

从而有

所以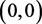 是一阶细焦点,由引理2知,
是一阶细焦点,由引理2知,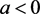 时原系统在原点稳定,
时原系统在原点稳定, 时原系统在原点不稳定。
时原系统在原点不稳定。
方法三(焦点量判别法):利用焦点量公式,由于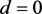 ,焦点量
,焦点量 ,所以
,所以 为一阶细焦点,当
为一阶细焦点,当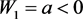 时
时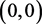 为稳定,当
为稳定,当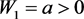 时
时 为不稳定。
为不稳定。
2) 接下来我们对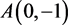 进行分析,首先作一线性变换 [3] [4] [5] [6]
进行分析,首先作一线性变换 [3] [4] [5] [6]
令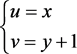 ,得
,得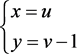 。
。
代入原系统,得到在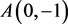 处的线性化方程
处的线性化方程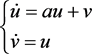 。
。
特征方程为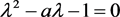 ,对应的特征根为
,对应的特征根为 ,两特征根为一正一负,故而
,两特征根为一正一负,故而
 是鞍点,此解是不稳定的。
是鞍点,此解是不稳定的。
3) 同理,对于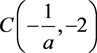 ,作一线性变换,令
,作一线性变换,令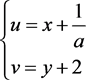 ,得
,得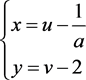 。
。
代入原系统,得到在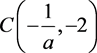 处的线性化方程
处的线性化方程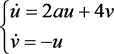 。
。
特征方程为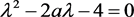 ,对应的特征根为
,对应的特征根为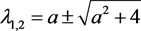 ,两特征根为一正一负,故
,两特征根为一正一负,故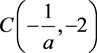
是鞍点,此解是不稳定的。
4) 对于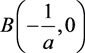 ,作一线性变换,令
,作一线性变换,令 ,得
,得 。
。
代入原系统,得到在 处的线性化方程
处的线性化方程 。
。
由于特征根为0,故而 是高阶奇点,经过线性变换得到的非线性系统为
是高阶奇点,经过线性变换得到的非线性系统为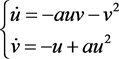
接下来判断其在原点的性态。
解:由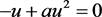 求函数
求函数 ,
,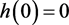 ,令
,令
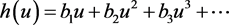
代入比较系数,易得: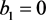 ,
, ,
,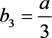 。于是
。于是

即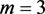 ,
, 。故而当
。故而当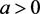 时原点为不稳定结点;当
时原点为不稳定结点;当 时原点为鞍点。
时原点为鞍点。
所以对于 ,当
,当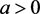 时为不稳定结点;当
时为不稳定结点;当 时为鞍点。
时为鞍点。
基金项目
山东省自然科学基金(ZR2018MA016)和国家自然科学基金(11601212)资助。