西江流域卫星遥感与水文模型模拟的两种土壤湿度对比研究

doi:10.12677/JWRR.2018.74038

期刊菜单

西江流域卫星遥感与水文模型模拟的两种土壤湿度对比研究
Comparison of Soil Moisture Sensed Remotely and Simulated by Hydrological Model in the Xijiang Basin

DOI: 10.12677/JWRR.2018.74038, PDF, HTML, XML, 被引量国家自然科学基金支持
作者: 曾凌, 熊立华, 杨涵：武汉大学水资源与水电工程科学国家重点实验室，湖北武汉
关键词: 水文模型；土壤湿度；卫星遥感；湿度指数；西江流域；Hydrologic Model； Soil Moisture； Satellite Remote Sensing； Soil Wetness Index； Xijiang Basin

摘要: 随着遥感技术的迅速发展，获取全球范围长时段卫星遥感土壤湿度产品成为可能，而目前卫星土壤湿度数据在水文建模领域的应用仍较少。本文采用DDRM (DEM-based distributed rainfall-runoff model)流域水文模型模拟了西江流域的土壤湿度的时空分布，同时采用ASCAT卫星遥感反演土壤湿度产品，推求了西江流域土壤湿度指数SWI (soil moisture index)的时空分布，在此基础上对比分析了这两种土壤湿度信息。结果表明：在流域面尺度和栅格点尺度上，水文模型模拟土壤湿度与卫星遥感土壤湿度指数的时间一致性均较好，在汛期二者的相关性要强于非汛期；水文模型模拟土壤湿度与卫星遥感土壤湿度指数在空间分布上较为一致。

Abstract: With the rapid development of remote sensing technology, a growing number of satellite-retrieved soil moisture products are available worldwide. However, there are few recent studies that focus on incor-porating these soil moisture products into hydrological modeling practice. In this study, the soil mois-ture simulated by the DEM-based distributed rainfall-runoff model (DDRM) was compared with the soil wetness index (SWI) derived from the ASCAT soil moisture product in the Xijiang basin in the southern China. The results indicate that the SWI series shows a close agreement with the simulated soil moisture series at both basin and cell scale. The correlation between the simulated soil moisture and the SWI series during the flood season (from April to September) is better when compared to that of the non-flood season. Besides, both soil moisture series show similar spatial distribution across the basin. These findings may serve as theoretical basis for further application of remotely sensed soil moisture product in hydrological modeling.

文章引用：曾凌, 熊立华, 杨涵. 西江流域卫星遥感与水文模型模拟的两种土壤湿度对比研究[J]. 水资源研究, 2018, 7(4): 339-350. https://doi.org/10.12677/JWRR.2018.74038

1. 引言

土壤水是自然界水循环与能量循环的重要组成部分，在下渗、蒸散发和径流等水文过程中起着重要作用。由于观测资料的极度缺乏，土壤湿度数据在水文领域的实际应用受到了限制。传统的土壤湿度信息获取主要依赖地面站网进行监测，该方式获取的土壤湿度信息具有较高精度，但其观测覆盖面小，代表性差，无法满足高时空分辨率的应用需求。与传统观测手段相比，遥感技术在覆盖范围和时效性等方面具备较大优势 [1] 。随着卫星遥感技术的快速发展以及相关土壤湿度数据产品的相继发布，分析区域乃至全球尺度土壤湿度的时空分布特征成为可能。同时，国内外不少研究致力于验证卫星遥感土壤湿度产品的精度和探究不同卫星产品在不同地区的适用性 [2] [3] [4] [5] 。

对于大部分具有物理机制的水文模型而言，土壤湿度作为一个重要中间过程变量，与模型产流计算密切相关。水文模型模拟的土壤湿度准确与否直接关系着模型的径流预测能力。目前，针对水文模型模拟土壤湿度与卫星遥感土壤湿度产品的对比分析较为缺乏，尤其是针对能模拟土壤湿度空间分布的分布式水文模型 [6] [7] 。基于上述问题，本文利用DDRM (DEM-based distributed rainfall-runoff model)模型模拟得到的西江流域土壤湿度，与欧洲航天局卫星遥感土壤湿度数据ASCAT进行验证，对比分析这两种土壤湿度数据的时空分布，为遥感土壤湿度数据在水文领域的应用提供理论依据。

2. 研究区域与数据

2.1. 研究区域概况

西江为珠江流域的主干流，位于东经102˚14'~114˚50'、北纬21˚31'~26˚49'之间，流经云南、贵州、广西与广东四省自治区。干流河长2075 km，集水面积为35.31万km²。流域内部多为丘陵和山地，平原面积小而分散。流域地形是自西北向东南倾斜，西北为云贵高原，东南为丘陵盆地，支流众多而且多为扇形流域，暴雨洪水产流集中，汇流速度快，各河流的上中游河床切割较深，下游逐渐平缓，致使西江中下游洪水一般都具有峰高量大、历时长、变幅大的特点 [8] 。西江流域属于热带、亚热带季风气候，雨季长但降水量年内分配极不均匀 [9] 。多年平均降水量在1000~2200 mm之间，年内降水量主要集中在汛期(4月~9月)，汛期降水量一般占全年的70%~80%左右，非汛期(10月~次年3月)降水量较少。

2.2. 土壤湿度数据

气象业务卫星MetOp (Meteorological Operational Satellite Program)，是欧洲第一颗致力于气象业务的极轨卫星。它提供了一系列连续、长期的数据集，用于监测全球气候以及提高天气预报精度 [10] 。MetOp系列卫星由三颗卫星组成，其中MetOp-A和MetOp-B已分别于2006年和2012年发射成功，MetOp-C预计将于2018年发射。ASCAT (Advanced SCATterometer)是MetOp系列卫星搭载的主动微波散射计，其本质为工作在5.255 GHz (C波段)频段上的真实孔径雷达，可测量地表后向散射系数。由后向散射系数反演得到土壤表层(<2 cm)水分饱和度，其取值范围为0%~100%。本文研究所用土壤湿度资料来源于欧洲气象业务化卫星MetOp-A，起止时间为2010年1月1日~2014年12月31日，资料空间分辨率为12.5 km。

2.3. 水文气象数据

本文采用的气象数据来源于西江梧州水文站控制区域内的35个中国地面气象站(如图1所示)的逐日观测资料(http://data.cma.cn/data/cdcdetail/dataCode/SURF_CLI_CHN_MUL_DAY_V3.0.html)，包括降水(mm)、气温(℃)、风速(m/s)和相对湿度(%)等，并由Penman-Monteith公式 [11] 推求逐日潜在蒸散发能力。逐日流量时间序列来源于梧州水文站实测资料。所有水文气象数据的起止时间均为2010年1月1日~2014年12月31日。

3. DDRM流域水文模型

熊立华等 [12] [13] 于2004年提出的DDRM流域水文模型，是一个基于栅格单元产流计算和栅格流向进行逐栅格分级汇流演算的分布式水文模型。构建DDRM模型时，须将整个流域划分为数个子流域，并在此基础上将各子流域进一步划分为大小相同的栅格单元 [12] [13] [14] [15] (如图2中所示)。该模型分布式汇流演算包括两个

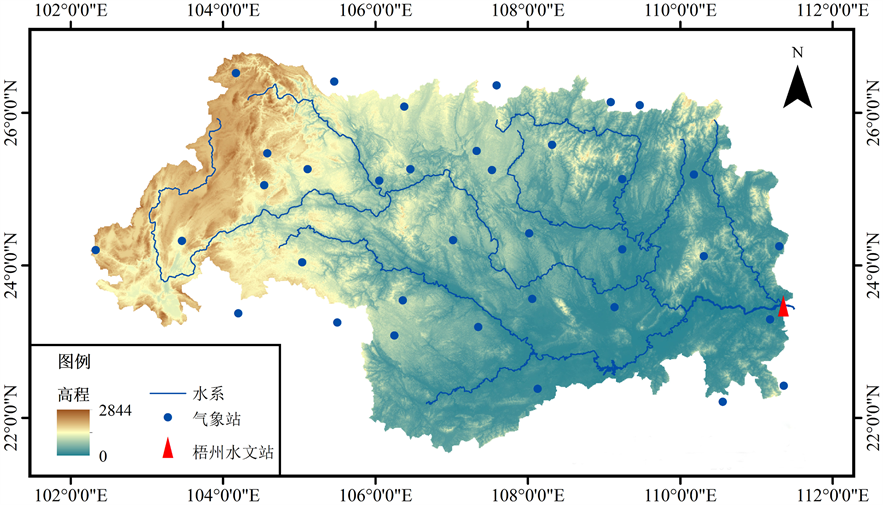
Figure 1. Location of the Xijiang basin and the gauges with hydrological and meteorological measurements

图1. 西江流域与水文气象观测站点

Figure 2. Discretization of basin into sub-basins and cells within DDRM model

图2. DDRM模型子流域和栅格划分示意图

阶段：首先基于DEM高程数据确定各子流域内栅格单元的汇流演算顺序，各栅格单元产流量按照栅格单元汇流演算顺序依次向下游栅格演算，直至子流域出口处；然后，各子流域出口节点处(节点d和e)流量再根据河网拓扑结构关系依次演算至流域出口处(节点f)。

DDRM模型的主体结构可分为三部分：栅格产流模块、栅格汇流模块和河网汇流模块。该模型假设对于流域内每一个栅格上存在3种不同的蓄水单元：河道、地下土壤和地表。为充分考虑流域内土壤蓄水能力的空间分布不均，模型假设栅格i处的土壤蓄水能力 $S M C_{i}$ 与对应的地形指数 [16] $T I_{i}$ 相关，采用如下的非线性关系式来表示：

$S M C_{i} = S 0 + {[\frac{T I_{i} - T I_{\min}}{T I_{\max} - T I_{\min}}]}^{n} \cdot S M$ (1)

式中：S0表示全流域最小蓄水能力，可取常数；SM表示全流域蓄水能力变化幅度； $T I_{\max}$ 和 $T I_{\min}$ 分别为流域最大和最小地形指数值；n为经验指数，需优选。当n取0时， $S M C_{i}$ 与地形指数无关，从而变成全流域均匀分布。

3.1. 栅格产流模块

模型栅格产流计算模块基于蓄满产流机制。对于栅格i，降水 $P_{i}$ 将直接进入土壤层，扣除蒸散发 $E T_{i}$ 后将补充地下水蓄水量 $S_{i}$ 。蒸散发的计算公式为：

$E T_{i, t} = \frac{S_{i, t}}{S M C_{i}} P E T_{i, t}$ (2)

式中：i为位置参数，t为时间参数， $P E T_{i, t}$ 为时刻t栅格i处的潜在蒸散发。

当地下水蓄水量低于栅格蓄水能力 $S M C_{i}$ 时，该栅格不产生地表径流。当地下水蓄水量超过该栅格蓄水能力 $S M C_{i}$ 时，剩余水量将涌入地表层形成浅层地表水 $S P_{i}$ ，浅层地表水蓄水量增加(如图3中所示)：

$S P_{i, t} = S P_{i, t - Δ t} + \max {[S_{i, t} - S M C_{i}], 0}$ (3)

浅层地表水在重力作用下将产生坡面流 $Q P_{i}$ ，并汇入栅格河道单元内。坡面流采用线性水库方法，计算公式为：

$Q P_{i, t} = \frac{S P_{i, t}}{T P}$ (4)

式中：TP为时间常数，反映坡面流出流特征，需优选。

Figure 3. Description of runoff generation calculation at cell-scale within DDRM model

图3. DDRM模型栅格单元产流计算示意图

栅格地下水出流特征不仅与栅格土壤蓄水量有关，还与地下水力坡度有关。DDRM模型假定地表坡度近似于地下水力坡度，并采用下式计算栅格地下水出流：

$Q G o u t_{i, t} = \frac{\max {[S_{i, t} - α \cdot S M C_{i}], 0}}{T S} {[\tan (\bar{β})]}^{b}$ (5)

式中： $α \cdot S M C_{i} (0 < α < 1)$ 为地下水出流阈值，当地下水水量超过该阈值时，栅格才产生地下水出流；TS为时间常数，反映地下水出流特征； $\bar{β}$ 表征栅格平均向下坡度；b反映坡度对地下水出流的影响，以上参数均需优选。

对于栅格i，其地下水入流为其上游各栅格地下水出流量之和，计算式为

$Q G i n_{i, t} = \sum_{j} Q G o u t_{j, t}$ (6)

由此，可得栅格i的地下土壤水量平衡方程：

$S_{i, t + Δ t} = S_{i, t} + [P_{i, t} - E T_{i, t}] \cdot Δ A \cdot Δ t + [Q G i n_{i, t} - Q G o u t_{i, t}] \cdot Δ t$ (7)

式中： $Δ A$ 和 $Δ t$ 分别为栅格单元面积和模型计算时间步长。

3.2. 栅格汇流模块

对于栅格i，其地表入流为其上游各栅格地表出流量之和，计算式为：

$Q i n_{i, t} = \sum_{j} Q o u t_{j, t}$ (8)

栅格间的河道单元流量演算采用马斯京根法，在考虑栅格坡面流的情况下，栅格河道出口流量计算如下：

$Q o u t_{i, t} = c_{0} [Q i n_{i, t} + Q P_{i, t}] + c_{1} [Q i n_{i, t - Δ t} + Q P_{i, t - Δ t}] + (1 - c_{0} - c_{1}) Q o u t_{i, t - Δ t}$ (9)

式中： $c_{0}$ 和 $c_{1}$ 为栅格河道马斯京根汇流参数。

3.3. 河网汇流模块

模型在每个子流域上分别进行栅格产汇流计算得到子流域出口流量，然后根据河网拓扑结构关系依次进行河网汇流演算。对每个河段，DDRM模型采用马斯京根法将河段上游节点的入流过程 $I_{t}$ 演算至下游节点的出流过程 $O_{t}$ ，计算公式为：

$O_{t} = h c_{0} I_{t} + h c_{1} I_{t - Δ t} + (1 - h c_{0} - h c_{1}) O_{t - Δ t}$ (10)

式中： $h c_{0}$ 和 $h c_{1}$ 为河网马斯京根汇流参数。值得一提的是，有些水文节点可能存在几条河段交汇(如图2所示)，此时应采用线性叠加方法，即认为汇流节点的流量是上游几个河段单独演算所得到的同时刻出口流量之和，计算式如下：

$O_{f, t} = O_{d f, t} + O_{e f, t} + Q o u t_{f, t}$ (11)

式中： $O_{f}$ 为节点f处总流量， $Q o u t_{f}$ 为节点f对应子流域(黄色区域)的出流量， $O_{d f}$ 和 $O_{e f}$ 分别为由节点d，e演算至节点f的流量，其计算式如下：

$O_{d f, t} = h c_{0} Q o u t_{d, t} + h c_{1} Q o u t_{d, t - Δ t} + (1 - h c_{0} - h c_{1}) O_{d f, t - Δ t}$ (12)

$O_{e f, t} = h c_{0} Q o u t_{e, t} + h c_{1} Q o u t_{e, t - Δ t} + (1 - h c_{0} - h c_{1}) O_{e f, t - Δ t}$ (13)

式中： $Q o u t_{d}$ 和 $Q o u t_{e}$ 分别为节点d，e所对应子流域(灰色区域和青色区域)的出流量， $h c_{0}$ 和 $h c_{1}$ 分别为河网马斯京根汇流参数，需优选。

3.4. 模型构建及参数率定

基于研究区域1 km分辨率栅格提取数字河网水系、确定各栅格汇流演算顺序，并在此基础上构建DDRM模型。对各站点的实测降水和潜在蒸散发能力应用反距离加权法进行空间插值，作为分布式模型的输入。由于可获取的研究区域水文气象资料长度有限，同时考虑本文的研究目标，将2010~2014年全部资料用于模型参数率定，不单独设置模型参数验证期。

采用Duan等 [17] 提出的SCE-UA算法进行模型参数率定，该算法是一种解决非线性约束最优化问题的有效方法，在水文模型领域已得到广泛应用。选取Nash-Sutcliffe效率系数(NSE)作为目标函数。

DDRM模型参数共有11个，其物理意义及率定得到的最优参数值如表1所示。

Table 1. Physical meaning and the optimal value of parameters within DDRM model

表1. DDRM模型参数物理意义及取值

4. 卫星遥感与水文模型模拟的土壤湿度对比分析

由于ASCAT土壤湿度数据反映的是土壤水分饱和度，不能与水文模型模拟土壤湿度序列(体积含水率)直接进行比较，故采用累积分布函数匹配(Cumulative Distribution Function Matching, CDFM)方法，将ASCAT土壤湿度数据校正到体积含水率数据范围内 [2] [18] ，校正后的ASCAT产品记作 $θ^{C D F M}$ 。此外，由于该卫星遥感土壤湿度产品只能反映土壤表层(<2 cm)的含水量情况，而DDRM模型模拟涉及到整个包气带，为使二者统一，采用土壤湿度指数(Soil Wetness Index, SWI)将卫星遥感土壤湿度信息延展到整个土壤剖面 [19] [20] 。SWI指标已被广泛证明能准确描述包气带的土壤湿度变化趋势，其计算公式如下：

$S W I_{i, t_{m}} = S W I_{i, t_{m - 1}} + K_{m} [S S M_{i, t_{m}} - S W I_{i, t_{m - 1}}]$ (14)

式中： $S S M_{i, t_{m}}$ 为时刻 $t_{m}$ 栅格i处卫星反演得到的表层土壤湿度， $K_{m}$ 为取值0~1之间的递归项，计算式为：

$K_{m} = \frac{K_{m - 1}}{K_{m - 1} + e^{- \frac{t_{m} - t_{m - 1}}{T}}}$ (15)

式中：T是以天为单位的土壤和气候特征常数。研究表明当 $T = 20 d$ 时，SWI能准确描述0~100 cm土层的土壤湿度变化 [19] 。由经CDFM校正后的ASCAT土壤湿度产品 $θ^{C D F M}$ 推求得到相应的SWI时间序列，记作 $θ^{S W I}$ 。

值得一提的是所采用的DDRM模型是基于1 km分辨率栅格构建的，为使水文模型模拟结果与卫星遥感产品相匹配，将水文模型模拟土壤湿度重采样至12.5 km分辨率。对于t时刻的栅格i，DDRM模型模拟的土壤湿度值 $θ_{i, t}^{D D R M}$ 由下式计算：

$θ_{i, t}^{D D R M} = \frac{S_{i, t}}{S M C_{i}}$ (16)

本文在流域面尺度和栅格点尺度上分析对比2010~2014年期间水文模型模拟以及卫星遥感土壤湿度。同时，为考虑年内降水量分配不均对水文模拟的影响，还对研究时期内汛期(4月~9月)及非汛期(10月~次年3月)的水文模型模拟以及卫星遥感土壤湿度分别进行对比。当涉及到栅格点尺度时，以流域内各栅格(以栅格i为例)的 $θ_{i, t}^{C D F M}$ 、 $θ_{i, t}^{S W I}$ 和 $θ_{i, t}^{D D R M}$ 为研究对象；考虑流域面尺度时，以流域面平均土壤湿度值、 ${\bar{θ}}_{\cdot, t}^{S W I}$ 和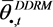序列为研究对象。时刻t流域面平均水文模型模拟土壤湿度值 ${\bar{θ}}_{\cdot, t}^{D D R M}$ 的计算式如下：

${\bar{θ}}_{\cdot, t}^{D D R M} = \frac{1}{M} \sum_{i}^{M} θ_{i, t}^{D D R M}$ (17)

式中：M为流域内栅格总数。 ${\bar{θ}}_{\cdot, t}^{C D F M}$ 和 ${\bar{θ}}_{\cdot, t}^{S W I}$ 的计算式与公式(17)类似。

采用相关系数(Correlation Coefficient, R)及均方根偏差(Root Mean Square Difference, RMSD)两个指标，对水文模型模拟以及卫星遥感土壤湿度时间一致性进行评价。在栅格点尺度上，两种指标的计算式如下：

$R_{i} = \frac{\sum_{t = 1}^{N} (θ_{i, t}^{D D R M} - {\bar{θ}}_{i, \cdot}^{D D R M}) (θ_{i, t}^{A S C A T} - {\bar{θ}}_{i, \cdot}^{A S C A T})}{\sqrt{\sum_{t = 1}^{N} {(θ_{i, t}^{D D R M} - {\bar{θ}}_{i, \cdot}^{D D R M})}^{2} \sum_{t = 1}^{N} {(θ_{i, t}^{A S C A T} - {\bar{θ}}_{i, \cdot}^{A S C A T})}^{2}}}$ (18)

$R M S D_{i} = \sqrt{\frac{1}{N} \sum_{t = 1}^{N} {(θ_{i, t}^{D D R M} - θ_{i, t}^{A S C A T})}^{2}}$ (19)

式中：i为位置参数，t为时间参数。 $θ_{i, t}^{A S C A T}$ 为栅格i处t时刻的卫星遥感土壤湿度值，可指代 $θ_{i, t}^{C D F M}$ 或 $θ_{i, t}^{S W I}$ 。 ${\bar{θ}}_{i, \cdot}^{A S C A T}$ 和 ${\bar{θ}}_{i, \cdot}^{D D R M}$ 分别表示栅格i处卫星遥感与水文模型模拟土壤湿度在统计时段内的均值。其中，， ${\bar{θ}}_{i, \cdot}^{A S C A T}$ 的计算式与之类似。N为统计时段数。

在流域面尺度上，两种指标的计算式分别为：

$R_{\cdot} = \frac{\sum_{t = 1}^{N} ({\bar{θ}}_{\cdot, t}^{D D R M} - {\bar{θ}}_{\cdot, \cdot}^{D D R M}) ({\bar{θ}}_{\cdot, t}^{A S C A T} - {\bar{θ}}_{\cdot, \cdot}^{A S C A T})}{\sqrt{\sum_{t = 1}^{N} {({\bar{θ}}_{\cdot, t}^{D D R M} - {\bar{θ}}_{\cdot, \cdot}^{D D R M})}^{2} \sum_{t = 1}^{N} {({\bar{θ}}_{\cdot, t}^{A S C A T} - {\bar{θ}}_{\cdot, \cdot}^{A S C A T})}^{2}}}$ (20)

$R M S D_{\cdot} = \sqrt{\frac{1}{N} \sum_{t = 1}^{N} {({\bar{θ}}_{\cdot, t}^{D D R M} - {\bar{θ}}_{\cdot, t}^{A S C A T})}^{2}}$ (21)

式中： ${\bar{θ}}_{\cdot, t}^{A S C A T}$ 为t时刻流域面平均卫星遥感土壤湿度值，可指代 ${\bar{θ}}_{\cdot, t}^{C D F M}$ 或 ${\bar{θ}}_{\cdot, t}^{S W I}$ 。 ${\bar{θ}}_{\cdot, \cdot}^{A S C A T}$ 和 ${\bar{θ}}_{\cdot, \cdot}^{D D R M}$ 分别表示流域面平均卫星遥感与水文模型模拟土壤湿度在统计时段内的均值。其中， ${\bar{θ}}_{\cdot, \cdot}^{D D R M} = \frac{1}{N} \sum_{t = 1}^{N} {\bar{θ}}_{\cdot, t}^{D D R M}$ ， ${\bar{θ}}_{\cdot, \cdot}^{A S C A T}$ 的计算式与之类似。

5. 结果分析

5.1. DDRM模型径流模拟结果

应用DDRM模型模拟了西江流域梧州水文站2010~2014年共5年的逐日径流量，模型模拟效果差强人意，NSE值为0.74。图4中给出了2012年全年梧州站实测径流与DDRM模型模拟径流。从图中可以看出径流模拟不足主要体现在洪水过程中洪峰量级不太准确。造成洪峰模拟效果偏差的主要原因有：1) 西江流域集水面积较大，而降水观测站点较为稀疏(仅35个)，导致空间插值得到的降水输入可能与实际情况有较大出入，从而降低了径流过程尤其是洪峰部分的模拟效果；2) 西江流域上游存在较大范围的岩溶石漠化区域，而DDRM未能够显式地考虑这种地质条件，从而影响了径流模拟效果。

5.2. 流域面尺度土壤湿度对比分析

首先比较了2010~2014年流域面尺度土壤湿度 ${\bar{θ}}_{\cdot, t}^{C D F M}$ 、 ${\bar{θ}}_{\cdot, t}^{S W I}$ 和 ${\bar{θ}}_{\cdot, t}^{D D R M}$ 序列整体以及在不同时期(汛期、非汛期)的时间一致性，如图5中所示。整体来看， ${\bar{θ}}_{\cdot, t}^{C D F M}$ 、 ${\bar{θ}}_{\cdot, t}^{S W I}$ 和 ${\bar{θ}}_{\cdot, t}^{D D R M}$ 的相关性较高，R值均大于0.70(显著性水平0.05)。对于非汛期与汛期， ${\bar{θ}}_{\cdot, t}^{C D F M}$ 、 ${\bar{θ}}_{\cdot, t}^{S W I}$ 和的相关程度亦令人满意，其中在汛期 ${\bar{θ}}_{\cdot, t}^{C D F M}$ 、 ${\bar{θ}}_{\cdot, t}^{S W I}$ 和 ${\bar{θ}}_{\cdot, t}^{D D R M}$ 的相关程度要优于非汛期。另外，由于SWI序列能代表整个包气带层的土壤湿度信息，无论在汛期还是非汛期， ${\bar{θ}}_{\cdot, t}^{S W I}$ 与 ${\bar{θ}}_{\cdot, t}^{D D R M}$ 序列的相关性(全部时期 $R = 0.78$ ；非汛期 $R = 0.61$ ；汛期 $R = 0.74$ )均较 ${\bar{θ}}_{\cdot, t}^{C D F M}$ 高。

图6中给出了2012年度流域面平均土壤湿度 ${\bar{θ}}_{\cdot, t}^{C D F M}$ 、 ${\bar{θ}}_{\cdot, t}^{S W I}$ 、 ${\bar{θ}}_{\cdot, t}^{D D R M}$ 序列与降水量序列。由图中可看出 ${\bar{θ}}_{\cdot, t}^{C D F M}$ 、 ${\bar{θ}}_{\cdot, t}^{S W I}$ 、 ${\bar{θ}}_{\cdot, t}^{D D R M}$ 序列与降水量序列年内变化趋势基本相同：有较大降水量时，三者均呈上升趋势；当降水量较小或者无降水时，三者均维持在某一水平或呈下降趋势。由于卫星遥感土壤湿度的CDFM校正值序列只针对土壤表层， ${\bar{θ}}_{\cdot, t}^{C D F M}$ 变化幅度相对较大。在汛期，在较大降水量的驱动下， ${\bar{θ}}_{\cdot, t}^{S W I}$ 与 ${\bar{θ}}_{\cdot, t}^{D D R M}$ 序列随时间变化幅度基本一致。在非汛期尤其是无降水时期，模型缺乏降水输入的情况下， ${\bar{θ}}_{\cdot, t}^{D D R M}$ 序列较为平坦，而 ${\bar{θ}}_{\cdot, t}^{S W I}$ 序列仍存在小幅波动，同时二者间还存在明显的相位差。由此可见，水文模型模拟的土壤湿度受降水量输入影响较大，因此其干旱时期土壤湿度模拟的可靠性需要进一步研究。

5.3. 栅格点尺度土壤湿度对比分析

由上文分析可知， $θ^{C D F M}$ 仅针对土壤表层，与能反映整个土层土壤湿度的 $θ^{S W I}$ 和 $θ^{D D R M}$ 有较大出入，因此

Figure 4. Observed runoff and DDRM simulated runoff at Wuzhou hydrologic station

图4. 梧州水文站实测与DDRM模型模拟流量过程

Figure 5. Consistency evaluation between basin-averaged soil moisture series during the whole period, the flood season and the non-flood season

图5. 不同时期流域面平均土壤湿度对比分析

Figure 6. Time series of basin-averaged soil moisture and rainfall during 2012

图6. 2012年度流域面平均土壤湿度和降水量时间序列

本节仅在栅格点尺度上对比分析 $θ^{S W I}$ 和 $θ^{D D R M}$ 。图7比较了 $θ^{S W I}$ 和 $θ^{D D R M}$ 在涨水时刻(2012/5/23)与退水时刻(2012/7/9)的空间分布情况。由图7中可看出，在涨水时刻和退水时刻， $θ^{S W I}$ 与 $θ^{D D R M}$ 的空间分布均较为吻合。在涨水时刻，土壤湿度值较大的栅格(蓝色)主要分布于流域中上游处。在退水时刻，全流域绝大部分栅格土壤湿度低于0.2 m³/m³ (绿色)。此时对于 $θ^{S W I}$ 和 $θ^{D D R M}$ 而言，土壤湿度值较大的栅格均零星地分布在流域下游位置。

为了进一步评价 $θ^{S W I}$ 与 $θ^{D D R M}$ 在栅格点尺度上的时间一致性，针对流域内栅格单元 $i (0 < i \leq M)$ 中的 $θ_{i, t}^{S W I}$ 与 $θ_{i, t}^{D D R M}$ 序列在不同时期(全部时期、非汛期和汛期)分别统计了两个评价指标 $R_{i}$ 和 $R M S D_{i}$ 。图8中给出了各时期栅格单元 $i (0 < i \leq M)$ 的 $θ_{i, t}^{S W I}$ 与 $θ_{i, t}^{D D R M}$ 序列相关系数 $R_{i}$ 值的空间分布。整体来看，对于流域内大部分栅格相关系数 $R_{i}$ 值都集中在0.50~0.90之间。在汛期，对于流域上游部分栅格，相关系数 $R_{i}$ 值接近0.90；而在非汛期，全流域范围内 $θ_{i, t}^{S W I}$ 与 $θ_{i, t}^{D D R M}$ 序列的相关关系较弱， $R_{i}$ 值集中在0.40~0.80。

图9中给出了不同时期栅格单元 $i (0 < i \leq M)$ 中 $θ_{i, t}^{S W I}$ 与 $θ_{i, t}^{D D R M}$ 序列的 $R M S D_{i}$ 值的空间分布。对于流域内绝大多数栅格而言，汛期的 $R M S D_{i}$ 值显著低于非汛期。在非汛期，流域下游处栅格 $R M S D_{i}$ 值均大于0.15 m³/m³；而在汛期，仅有流域下游部分栅格的 $R M S D_{i}$ 值大于0.15 m³/m³。值得一提的是西江流域下游主要位于广西壮族自治区境内，该区域内城镇化面积及耕作面积较大，其水文条件与流域内其他区域(主要为林地)存在差别，导致水文模型模拟的土壤湿度可能与实际情况不符。

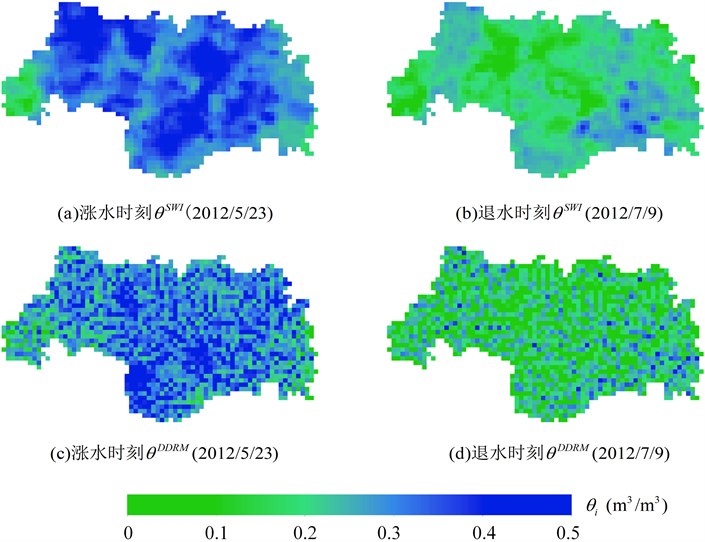
Figure 7. Spatial distribution of $θ^{S W I}$ and $θ^{D D R M}$ at the moment of flood rising and recession

图7. 涨水时刻与退水时刻 $θ^{S W I}$ 和 $θ^{D D R M}$ 空间分布

Figure 8. Spatial distribution of correlation coefficient between time series of $θ_{i, t}^{S W I}$ and $θ_{i, t}^{D D R M}$ at cell-scale during the whole period, the flood season and the non-flood season

图8. 不同时期栅格点尺度 $θ_{i, t}^{S W I}$ 和 $θ_{i, t}^{D D R M}$ 序列相关系数值空间分布

Figure 9. Spatial distribution of RMSD between time series of $θ_{i, t}^{S W I}$ and $θ_{i, t}^{D D R M}$ at cell-scale during the whole period, the flood season and the non-flood season

图9. 不同时期栅格尺度 $θ_{i, t}^{S W I}$ 和 $θ_{i, t}^{D D R M}$ 序列均方根偏差值空间分布

6. 结语

本文基于DDRM模型模拟了西江流域2010~2014年的径流过程及同时期土壤湿度，并将模拟得到的土壤湿度时间序列，与ASCAT卫星遥感土壤湿度产品推求的土壤湿度指数序列进行对比分析。结果表明：流域平均模型模拟土壤湿度与土壤湿度指数序列相关性较高，且随时间变化趋势基本一致。此外，水文模型模拟土壤湿度与土壤湿度指数在空间分布上吻合度较高。

随着卫星遥感技术的不断提高及卫星遥感产品的不断拓展升级，越来越多的卫星遥感产品(如降水、蒸发和土壤湿度等)必将被引入到水文建模领域中。本文分析了模型模拟土壤湿度与卫星遥感土壤湿度的时间一致性，这可能为卫星遥感土壤湿度产品在水文领域的应用(如土壤湿度数据同化、模型参数率定等)提供理论支撑。如何更大程度的有效利用这些卫星遥感数据，为水文建模以及水文预报更好地服务，亟待更加深入的研究。

基金项目

国家重点研发计划项目(2017YFC0405901)和国家自然科学基金项目(51525902)。

参考文献

参考文献

[1]	黄图南, 郑有飞, 段长春, 尹继福, 吴荣军. 几种卫星反演土壤湿度在中国地区的对比分析[J]. 遥感信息, 2017(3): 25-33. HUANG Tunan, ZHENG Youfei, DUAN Changchun, YIN Jifu, WU Rongjun. Comparative analysis of soil moisture retrieval by satellites in China. Remote Sensing Information, 2017(3): 25-33. (in Chinese)
[2]	庄媛, 师春香, 沈润平, 姜立鹏, 王杉. 中国区域多种微波遥感土壤湿度产品质量评估[J]. 气象科学, 2015(3): 289-296. ZHUANG Yuan, SHI Chunxiang, SHEN Runping, JIANG Lipeng, WANG Shan. Quality evaluation of multi-microwave remote sensing soil moisture products over China. Journal of the Meteorological Science, 2015(3): 289-296. (in Chi-nese)
[3]	RÖTZER, K., MONTZKA, C., BOGENA, H., WAGNER, W., KERR, Y. H., KIDD, R. and VEREECKEN, H. Catchment scale validation of SMOS and ASCAT soil moisture products using hydrological modeling and temporal stability analysis. Journal of Hydrology, 2014, 519: 934-946. https://doi.org/10.1016/j.jhydrol.2014.07.065
[4]	马思源, 朱克云, 李明星, 马柱国. 中国区域多源土壤湿度数据的比较研究[J]. 气候与环境研究, 2016, 21(2): 121-133. MA Siyuan, ZHU Keyuan, LI Mingxing, MA Zhuguo. A comparative study of multi-source soil moisture data for China’s regions. Climatic and Environmental Research, 2016, 21(2): 121-133. (in Chinese)
[5]	李明星, 马柱国, 杜继稳. 区域土壤湿度模拟检验和趋势分析——以陕西省为例[J]. 中国科学:地球科学, 2010(3): 363-379. LI Mingxing, MA Ghuguo, DU Jiwen. Regional soil moisture simulation for Shaanxi Province using SWAT model validation and trend analysis. Science China Earth Sciences, 2010(3): 363-379. (in Chinese)
[6]	LAIOLO, P., GABELLANI, S., CAMPO, L., SILVESTRO, F., DELOGU, F., RUDARI, R., PULVIRENTI, L., BONI, G., FASCETTI, F. and PIERDICCA, N. Impact of different satellite soil moisture products on the predictions of a continuous distributed hydrological model. International Journal of Applied Earth Observation and Geoinformation, 2016, 48: 131-145. https://doi.org/10.1016/j.jag.2015.06.002
[7]	XIONG, L., YANG, H. and ZENG, L. Evaluating Consistency between the remotely sensed soil moisture and the hydrological model-simulated soil moisture in the Qujiang catchment of China. Water, 2018, 10(3): 291. https://doi.org/10.3390/w10030291
[8]	WAGNER, W., HAHN, S., KIDD, R., MELZER, T., BARTALIS, Z., HASENAUER, S., FIGA-SALDAÑA, J., DE ROSNAY, P., JANN, A., SCHNEIDER, S., KOMMA, J., KUBU, G., BRUGGER, K., AUBRECHT, C., ZÜGER, J., GANGKOFNER, U., KIENBERGER, S., BROCCA, L., WANG, Y., BLÖSCHL, G., EITZINGER, J. and STEINNOCHER, K. The ASCAT soil moisture product: A review of its specifications, validation results, and emerging applications. Meteorologische Zeitschrift, 2013, 22(1): 5-33. https://doi.org/10.1127/0941-2948/2013/0399
[9]	张峰. 西江流域分布式水文模拟及其应用研究[D]. 东华大学, 2012. ZHANG Feng. Research on distributed hydrological simulation and its application in Xijiang River Basin. Donghua University, 2012. (in Chinese)
[10]	孙龙. 西江中下游洪水预报系统研究[D]. 河海大学, 2007. SUN Long. Study on the flood forecasting system in the middle and lower reaches of Xijiang Watershed. Hohai University, 2007. (in Chinese)
[11]	ALLEN, R. G., PEREIRA, L. S., RAES, D. and SMITH, D. Crop evapotranspiration-guidelines for computing crop water requirements-FAO Irrigation and drainage paper 56. FAO, Rome, 1998, 300(9): D05109.
[12]	熊立华, 郭生练. 分布式流域水文模型[M]. 北京: 中国水利水电出版社, 2004. XIONG Lihua, GUO Shenglian. Distributed hydrological model. Beijing: China Water and Power Press, 2004. (in Chi-nese)
[13]	熊立华, 郭生练, 田向荣. 基于DEM的分布式流域水文模型及应用[J]. 水科学进展, 2004, 15(4): 517-520. XIONG Lihua, GUO Shenglian, TIAN Xiangrong. DEM-based distributed hydrological model and its application. Advances in Water Science, 2004, 15(4): 517-520. (in Chinese)
[14]	龙海峰, 熊立华, 万民. 基于DEM的分布式水文模型在清江流域的应用[J]. 长江流域资源与环境, 2012, 21(1): 71-78. LONG Haifeng, XIONG Lihua, WAN Min. Application of DEM-based distributed hydrological model in Qingjiang River Basin. Resources and Environment in the Yangtze Basin, 2012, 21(1): 71-78. (in Chinese)
[15]	万民, 熊立华, 董磊华. 飞来峡流域基于栅格DEM的分布式水文模拟[J]. 武汉大学学报(工学版), 2010, 43(5): 549-553. WAN Min, XIONG Lihua, DONG Leihua. Grid DEM-based distributed hydrological modeling for Feilaixia watershed. Engineering Journal of Wuhan University, 2010, 43(5): 549-553. (in Chinese)
[16]	BEVEN, K. J. Distributed hydrological modeling: Application of the TOPMODEL concept. New York: John Wiley & Sons Limited, 1997.
[17]	DUAN, Q., SOROOSHIAN, S. and GUPTA, V. Effective and efficient global optimization for conceptual rainfall-runoff models. Water Resources Research, 1992, 28(4): 1015-1031. https://doi.org/10.1029/91WR02985
[18]	LIU, Y. Y., PARINUSSA, R. M., DORIGO, W. A., De JEU, R. A. M., WAGNER, W., Van Dijk, A. I. J. M., Mccabe, M. F. and EVANS, J. P. Developing an improved soil moisture dataset by blending passive and active microwave satellite-based retrievals. Hydrology and Earth System Sciences, 2011, 15(2): 425. https://doi.org/10.5194/hess-15-425-2011
[19]	WAGNER, W., LEMOINE, G., ROTT, H. A method for estimating soil moisture from ERS Scatterometer and soil data. Remote Sensing of Environment. 1999, 70: 191-207.
[20]	蒋冲, 王飞, 穆兴民, 李锐. 土壤湿度指数在黄土高原的适宜性评价[J]. 灌溉排水学报, 2012(3): 31-36. JIANG Chong, WANG Fei, MU Xingmin, LI Rui. Evaluation of the soil water index and surface soil moisture on the Loess Plateau. Journal of Irrigation and Drainage, 2012(3): 31-36. (in Chinese).

为你推荐

友情链接