求非线性方程重根的区间算法

Interval Algorithm of Nonlinear Equation with Multiple Root

摘要: 本文主要研究非线性方程重根问题的求解方法。基于区间分析理论和函数的二阶近似逼近，设计了一种求解非线性方程重根问题的新方法，并进行了相关的收敛性分析，给出了近似解在数值上的误差估计，最后通过数值算例与传统的区间迭代法进行了对比。新方法不仅能解决非线性方程的单根问题，而且能有效解决非线性方程的二重根问题，且计算量较小，收敛速度较快，数值结果有效可靠。

Abstract: This article mainly discusses methods for solving nonlinear equation. Based on theory of interval analysis and the second order approximate approach, a new method is proposed to solve nonlinear equation with multiple root, carrying related convergence analysis, giving numerical error estimation of approximate solution, contract with traditional method though several numerical examples at last. It can not only solve nonlinear equation with simple root but also solve nonlinear equation with double root efficiently. At the same time, the new method needs less amount of computation and has fast convergence; the numerical results are effective and reliable.

1. 引言

非线性方程的求根问题是数值分析的一个基本问题。1966年，Moore [1] 提出的二次收敛的古典区间牛顿法是一种重要的方法，但是该方法要求 $0\notin F^{\prime }\left(X^{\left(0\right)}\right)$ ，对于求重根的情况，此时， $0\in F^{\prime }\left(X^{\left(k\right)}\right),k=0,1,2,\cdots$ ，该方法不再适用。

对于 $0\in F^{\prime }\left(X^{\left(0\right)}\right)$ 的情况，Hansen [2] 对古典的区间Newton法做了有效的改进，给出了在相应初始区间始终收敛的区间Newton法。改进的区间Newton法，仅需在初始迭代区间存在有限个实根，无论这些实根的重数是多少，均可以有效计算初始区间的所有根，而且可以推广到高维的情形。但是应用改进的区间Newton法来求解非线性方程的重根问题时，其收敛速度将变得很慢。

在实际应用中，遇到的问题可能是求方程的单根，也可能是求方程的重根。现有的许多高阶收敛的区间迭代法 [6] - [15] 在求解方程单根时表现出非常好的数值结果，但当求解的是非线性方程的重根时，其计算效率就会大大下降。

在本文中，我们引入以下符号说明： $I\left(R\right)$ 表示R上所有区间的集合，关于区间 $X=\left[\underset{\_}{x},\bar{x}\right]=\left\{x\in R|\underset{\_}{x}\le x\le \bar{x}\right\}$ (如果 $\bar{x}=\underset{\_}{x}=x$ ，则 $X=\left[\underset{\_}{x},\bar{x}\right]=\left[x,x\right]=x$ 退化为一个点)，称 $m\left(X\right)=\frac{\bar{x}+\underset{\_}{x}}{2}$ 为区间X的中点， $W\left(X\right)=\bar{x}-\underset{\_}{x}$ 为区间X的宽度， $\left|X\right|=\max \left\{\left|\underset{\_}{x}\right|,\left|\bar{x}\right|\right\}$ 为区间X的绝对值。与本文相关的其它区间分析的内容可参阅文献 [1] - [6] 等。

定义1：设 $f:R\to R$ ，若存在区间值映射 $F:I\left(R\right)\to I\left(R\right)$ ，对任意 $x\in X\subseteq I\left(R\right)$ ，有 $F\left(\left[x,x\right]\right)=f\left(x\right)$ 成立，则称区间值映射 $F\left(X\right)$ 为函数 $f\left(x\right)$ 的区间扩展。相对应， $F^{\prime }\left(X\right)$ 为导函数 $f^{\prime }\left(x\right)$ 的区间扩展， $F^{″}\left(X\right)$ 为二阶导数 $f^{″}\left(x\right)$ 的区间扩展。

定义2：设区间值映射 $F:I\left(R\right)\to I\left(R\right)$ 为函数f的区间扩展，而 $X,Y\in I\left(R\right)$ 且满足 $X\subseteq Y$ ，如果成立 $F\left(X\right)\subseteq F\left(Y\right)$ ，则称区间值映射F具有包含单调性。

2. Hansen改进的区间Newton法

古典区间Newton法是求解非线性方程的经典方法。设f是单变量实值的连续可微函数， $F^{\prime }\left(X\right)$ 是 $f^{\prime }\left(x\right)$ 在区间X上具有包含单调性的区间扩展，记 $F^{\prime }\left(X^{\left(0\right)}\right)$ 为函数 $f^{\prime }\left(x\right)$ 在给定区间 $X^{\left(0\right)}$ 上的区间扩展，如果 $0\notin F^{\prime }\left(X^{\left(0\right)}\right)$ ，则可建立如下迭代公式

$X^{\left(k+1\right)}=X^{\left(k\right)}\cap N\left(X^{\left(k\right)}\right),k=0,1,2,\cdots$

这里

$N\left(X^{\left(k\right)}\right)=m\left(X^{\left(k\right)}\right)-\frac{f\left(m\left(X^{\left(k\right)}\right)\right)}{F^{\prime }(X^{(k))}}$

这就是著名的古典区间Newton法 [1] [2] [3] [4] 。

当 $0\in F^{\prime }\left(X^{\left(k\right)}\right)$ 时，Hansen通过引进无界区间的概念来定义区间除法。

设 $F^{\prime }\left(X^{\left(k\right)}\right)=\left[c_k,d_k\right]$ ，因为 $0\in \left[c_k,d_k\right]$ ，定义

$\frac{1}{F^{\prime }\left(X^{\left(k\right)}\right)}=\{\begin{array}{l}\left[\frac{1}{d_k},\infty \right]c_k=0\\ \left[-\infty ,\frac{1}{c_k}\right]d_k=0\\ \left[-\infty ,\frac{1}{c_k}\right]\cup \left[\frac{1}{d_k},\infty \right]其它情况\end{array}$

若成立 $f\left(m\left(X^{\left(k\right)}\right)\right)=0$ ，则 $m\left(X^{\left(k\right)}\right)$ 就是f的零点，否则 $H\left(X^{\left(k\right)}\right)$ 就有两种可能的定义，

1) 对于 $f\left(m\left(X^{\left(k\right)}\right)\right)>0$ 的情形，有

$H\left(X^{\left(k\right)}\right)=\{\begin{array}{l}\left[-\infty ,q_k\right]c_k=0\\ \left[p_k,\infty \right]d_k=0\\ \left[-\infty ,q_k\right]\cup \left[p_k,\infty \right]其它情况\end{array}$

2) 对于 $f\left(m\left(X^{\left(k\right)}\right)\right)<0$ 的情形，有其它情况

$H\left(X^{\left(k\right)}\right)=\{\begin{array}{l}[q_k,\infty ]c_k=0\\ [-\infty ,p_k]d_k=0\\ \left[-\infty ,p_k\right]\cup \left[q_k,\infty \right]其它情况\end{array}$

其中 $\begin{array}{l}{p}_k=m\left(X^{\left(k\right)}\right)-f\left(m\left(X^{\left(k\right)}\right)\right)/c_k\\ q_k=m\left(X^{\left(k\right)}\right)-f\left(m\left(X^{\left(k\right)}\right)\right)/d_k\end{array}$

当 $0\notin F^{\prime }\left(X^{\left(k\right)}\right)$ 时，有

$H\left(X^{\left(k\right)}\right)=m\left(X^{\left(k\right)}\right)-\frac{f\left(m\left(X^{\left(k\right)}\right)\right)}{F^{\prime }(X^{(k))}}$

此时

$X^{\left(k+1\right)}=X^{\left(k\right)}\cap H\left(X^{\left(k\right)}\right),k=0,1,2,\cdots$

即为Hansen [2] 改进的区间Newton法。

3. 新的区间迭代算法

对于非线性方程 $f\left(x\right)=0$ ，设 $x^{*}$ 为该方程的单根或重根， $x_0$ 是比较靠近 $x^{*}$ 的初始值。使用泰勒公式将 $f\left(x\right)=0$ 展开到二阶，有

$f\left(x_0\right)+\left(x-x_0\right)f^{\prime }\left(x_0\right)+\frac{1}{2}{\left(x-x_0\right)}^2{f}^{″}\left(\xi \right)=0$ (1)

这是一个关于x的二次方程且一定存在实根，解得

$x=x_0-\frac{f^{\prime }\left(x_0\right)-\sqrt{{\left[f^{\prime }\left(x_0\right)\right]}^2-2f\left(x_0\right)f^{″}\left(\xi \right)}}{f^{″}\left(\xi \right)}$ (2)

或

$x=x_0-\frac{f^{\prime }\left(x_0\right)+\sqrt{{\left[f^{\prime }\left(x_0\right)\right]}^2-2f\left(x_0\right)f^{″}\left(\xi \right)}}{f^{″}\left(\xi \right)}$ (3)

设 $F^{″}\left(X\right)$ 为 $f^{″}\left(x\right)$ 的具有包含单调性的区间扩展，新的区间迭代法如下

$X^{\left(k+1\right)}=X^{\left(k\right)}\cap S\left(X^{\left(k\right)}\right)$ (4)

这里

$S\left(X^{\left(k\right)}\right)=m\left(X^{\left(k\right)}\right)-\frac{f^{\prime }\left(m\left(X^{\left(k\right)}\right)\right)-\sqrt{{\left[f^{\prime }\left(m\left(X^{\left(k\right)}\right)\right)\right]}^2-2f\left(m\left(X^{\left(k\right)}\right)\right)F^{″}\left(X^{\left(k\right)}\right)}}{F^{″}\left(X^{\left(k\right)}\right)}$ (5)

或

$S\left(X^{\left(k\right)}\right)=m\left(X^{\left(k\right)}\right)-\frac{f^{\prime }\left(m\left(X^{\left(k\right)}\right)\right)+\sqrt{{\left[f^{\prime }\left(m\left(X^{\left(k\right)}\right)\right)\right]}^2-2f\left(m\left(X^{\left(k\right)}\right)\right)F^{″}\left(X^{\left(k\right)}\right)}}{F^{″}\left(X^{\left(k\right)}\right)}$ (6)

4. 新方法的收敛性与误差分析

说明：以上区间算子S有两种，所用方法完全相同，所以以下定理只就第一种情况进行证明，第二种情况的证明步骤也完全相同，就不作详叙。

定理1：设f为给定区间 $X^{\left(0\right)}$ 上的一个二阶连续可微函数，且 $0\notin F^{″}\left(X^{\left(k\right)}\right),k=0,1,2,\cdots$ 如果 $X^{\left(0\right)}$ 包含有f的一个零点 $x^{*}$ ，则所有的 $X^{\left(k\right)},k=0,1,2,\cdots$ 都包含 $x^{*}$ ，且有 $X^{\left(k\text{+1}\right)}\subseteq X^{\left(k\right)},x^{*}\in {\displaystyle \underset{k=0}{\overset{\infty }{\cap }}{X}^{\left(k\right)}}$ 。

证明：由式(2)可知

$\begin{array}{c}{x}^{*}=m\left(X^{\left(0\right)}\right)-\frac{f^{\prime }\left(m\left(X^{\left(0\right)}\right)\right)-\sqrt{{\left[f^{\prime }\left(m\left(X^{\left(0\right)}\right)\right)\right]}^2-2f\left(m\left(X^{\left(0\right)}\right)\right)f^{″}\left(\xi \right)}}{f^{″}\left(\xi \right)}\\ \in m\left(X^{\left(0\right)}\right)-\frac{f^{\prime }\left(m\left(X^{\left(0\right)}\right)\right)-\sqrt{{\left[f^{\prime }\left(m\left(X^{\left(0\right)}\right)\right)\right]}^2-2f\left(m\left(X^{\left(0\right)}\right)\right)F^{″}\left(X^{\left(0\right)}\right)}}{F^{″}(X^{(0)})}\end{array}$

故 $x^{*}\in X^{\left(0\right)}\cap S\left(X^{\left(0\right)}\right)=X^{\left(1\right)}$ 。

同理，如果 $x^{*}\in X^{\left(k\right)}$ ，则 $x^{*}\in X^{\left(k+1\right)}$ ，由数学归纳法可得

$x^{*}\in X^{\left(k\right)},k=0,1,\cdots$

所以 $x^{*}\in {\displaystyle \underset{k=0}{\overset{\infty }{\cap }}{X}^{\left(k\right)}}$ ，由式(4)可得 $X^{\left(k+1\right)}\subseteq X^{\left(k\right)}$ 。

该区间算子的好处在于：1) 能检测到一个区间是否有根存在，这样可以避免无用的迭代运算；2) 能保证在一个区间有且只有一个实根。

定理2：设f为给定区间 $X^{\left(0\right)}$ 上的一个二阶连续可微函数，且 $0\notin F^{″}\left(X\right)$ ，则

1) 如果 $S\left(X\right)\subseteq X$ ，则X中有且仅有方程 $f\left(x\right)=0$ 的一实根。

2) 如果 $X\cap S\left(X\right)=\varphi$ ，则X中不含方程 $f\left(x\right)=0$ 的任何实根。

证明：1)首先证明方程 $f\left(x\right)=0$ 根的存在性，

对任意实数 $y\in X$ ，构造算子 $\tilde{S}\left(y\right)=y-\frac{f^{\prime }\left(y\right)-\sqrt{{\left[f^{\prime }\left(y\right)\right]}^2-2f\left(y\right)l\left(y,m\left(X\right)\right)}}{l(y,m(X))}$

其中 $l\left(y,m\left(X\right)\right)=\{\begin{array}{l}\frac{f^{\prime }\left(y\right)-f^{\prime }\left(m\left(X\right)\right)}{y-m\left(X\right)},y\ne m\left(X\right)\\ f^{″}\left(y\right),y=m(X)\end{array}$

由于 $f^{\prime }\left(x\right),f^{″}\left(x\right)$ 在X上的连续，以及 $0\notin F^{″}\left(X\right)$ ，所以 $\tilde{S}\left(y\right)$ 为定义在X的连续算子，当 $y=m\left(X\right)$ 时，由 $F^{″}\left(X\right)$ 的包含单调性可知

$\tilde{S}\left(y\right)=y-\frac{f^{\prime }\left(m\left(X\right)\right)-\sqrt{{\left[f^{\prime }\left(m\left(X\right)\right)\right]}^2-2f\left(m\left(X\right)\right)f^{″}\left(m\left(X\right)\right)}}{f^{″}\left(m\left(X\right)\right)}\in S(X)$

当 $y\ne m\left(X\right)$ 时，化简可得 $\tilde{S}\left(y\right)\in S\left(X\right)$ ，又因为 $S\left(X\right)\subseteq X$ ，则区间算子 $\tilde{S}$ 是将X变换到其自身的连续算子，且区间X为有界闭凸集，根据Browner不动点定理，可知 $\tilde{S}$ 存在不动点 $x^{*}\in X$ ，使得 $\tilde{S}\left(x^{\ast }\right)=x^{\ast }$ ，从而有

$\frac{f^{\prime }\left(x^{*}\right)-\sqrt{{\left[f^{\prime }\left(x^{*}\right)\right]}^2-2f\left(x^{*}\right)l\left(y,m\left(X\right)\right)}}{l\left(y,m\left(X\right)\right)}=0$

因为 $0\notin F^{″}\left(X\right)$ ，所以 $l\left(y,m\left(X\right)\right)\ne 0$ ，故有 $f\left(x^{*}\right)=0$ 。

下面证方程 $f\left(x\right)=0$ 根的唯一性，如果 $m\left(X^{\left(k\right)}\right)$ 是函数f的零点，成立

$m\left(X^{\left(k\right)}\right)=S\left(X^{\left(k\right)}\right)=S\left(m\left(X^{\left(k\right)}\right)\right)$

则有 $m\left(X^{\left(k\right)}\right)=X^{\left(k\right)}\cap S\left(m\left(X^{\left(k\right)}\right)\right)$ ，这表明程序终止在有限步。

如果 $m\left(X^{\left(k\right)}\right)$ 不是f的零点，此时，由 $S\left(X^{\left(k\right)}\right)$ 的定义可知总有 $S\left(X^{\left(k\right)}\right)>m\left(X^{\left(k\right)}\right)$ 或 $S\left(X^{\left(k\right)}\right)<m\left(X^{\left(k\right)}\right)$ 成立，这表明 $S\left(X^{\left(k\right)}\right)$ 不包含 $X^{\left(k\right)}$ 的中点，因此必有 $W\left(X^{\left(k+1\right)}\right)<\frac{1}{2}W\left(X^{\left(k\right)}\right)$ ，从而，故由根的存在性可知点收敛于。

综上可得X中有且仅有的一个零点。

2) 若X包含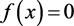的零点，由定理1的证明可知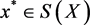，故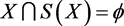与条件矛盾，所以X中不含的零点。

定理3：设f为给定区间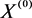上的一个二阶连续可微函数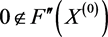，且方程存在唯一的重根 (至少二重)。如果且为Lipschitz区间函数，则由迭代公式(4)所得区间列二次收敛，即存在常数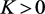，使得

.

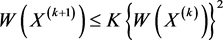证明：因为为Lipschitz区间函数，则存在，使得

且

，

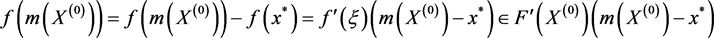所以

.

又因为，则存在，使得，且

故

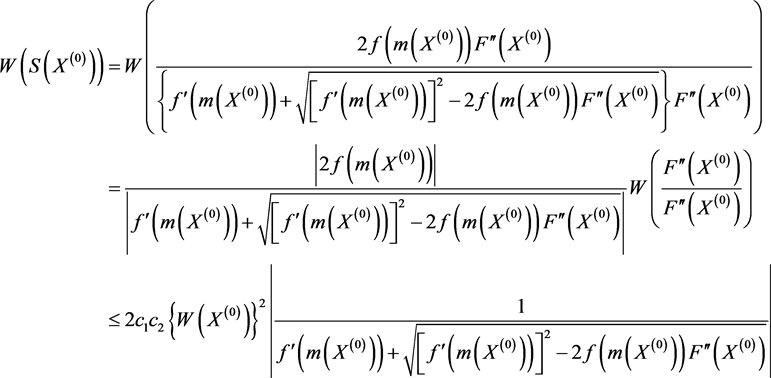
这里，存在常数使得

.

综上可得，令，则有

Table 1. Numerical comparison of both HM method and SM method

表1. HM和SM两种方法的数值对比

.

同理有。

5. 数值算例及结果分析

为了验证本文方法的正确性，在联想G400笔记本电脑(处理器：英特尔第三代酷睿i5-3230M @ 2.60 GHz双核)上借助MATLAB R2012b与工具箱INTLAB_V5.5进行编程求解。下面将给出一些数值算例，分别应用本文的方法与Hansen改进的区间Newton法来求解，并对结果进行了对比分析，其中，“HM”表示Hansen改进的区间Newton法，“SM”表示本文的方法，ε表示精度，N表示迭代次数time表示迭代所用时间(单位为秒)，X表示计算结果(表1)。

具体算例和数值计算结果如下：

例1：求方程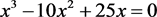在区间上的根，方程的准确重根为。

例2：求方程在区间上的根，方程的准确重根为。

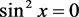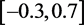例3：求方程在区间上的根，方程的准确重根为。

例4：求方程在区间上的根，方程的准确重根为。

例5：求方程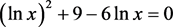在区间上的根，方程的准确重根为。

例6：求方程在区间上的根，方程的准确重根为。

例7：求方程在区间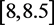上的根，方程的准确重根为。

上述数值算例的结果以及更多的数值计算结果都验证了，在求解非线性方程的重根问题中，本文所建立的区间迭代法与Hansen改进的区间Newton法相比，在迭代次数和时间花费上具有更好的优势，这充分证明了本文方法是有效可靠的。

基金项目

本文工作由江苏省自然科学基金(No. BK20151139)支持。